一、有限状态自动机
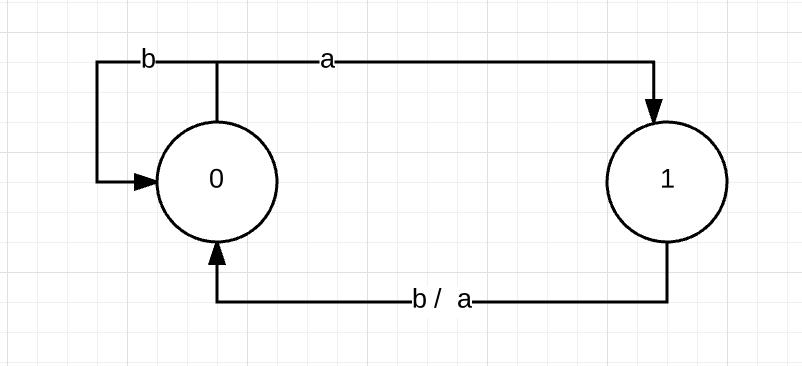
图中两个圆圈,也叫节点,用于表示状态,从图中可以看成,它有两个状态,分别叫0和1。从每个节点出发,都会有若干条边。当处于某个状态时,如果输入的字符跟该节点出发的某条边的内容一样,那么就会引起状态的转换。例如,如果当前状态处于0,输入是字符a,那么状态机就会从状态0进入状态1。如果当前状态是1,输入字符是b或a,那么,状态机就会从状态1进入状态0。如果当前所处的状态,没有出去的边可以应对输入的字符,那么状态机便会进入到错误状态。例如,如果当前处于状态0,输入字符是c,那么状态机就会出错,因为从状态0开始,没有哪条边对应的字符是c。
本代码的运行效果:
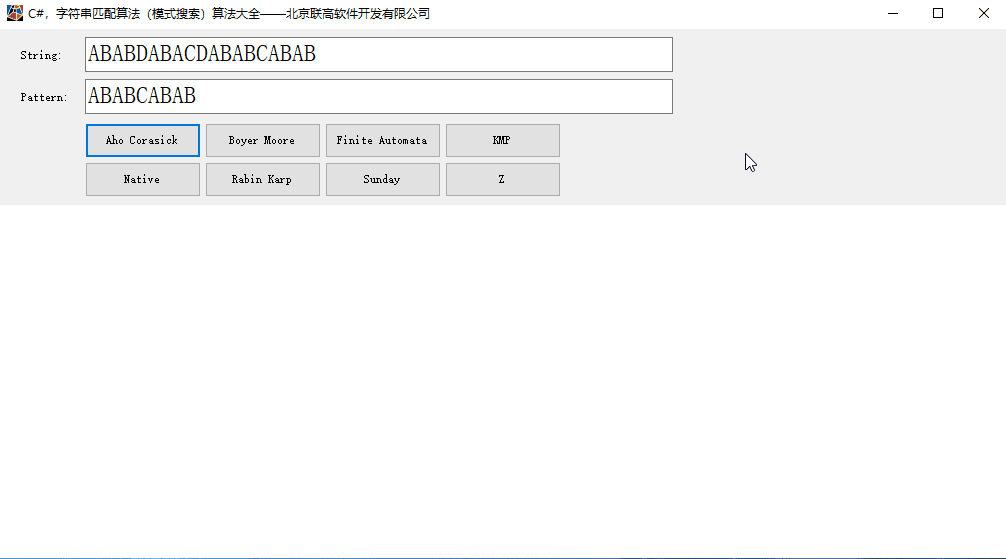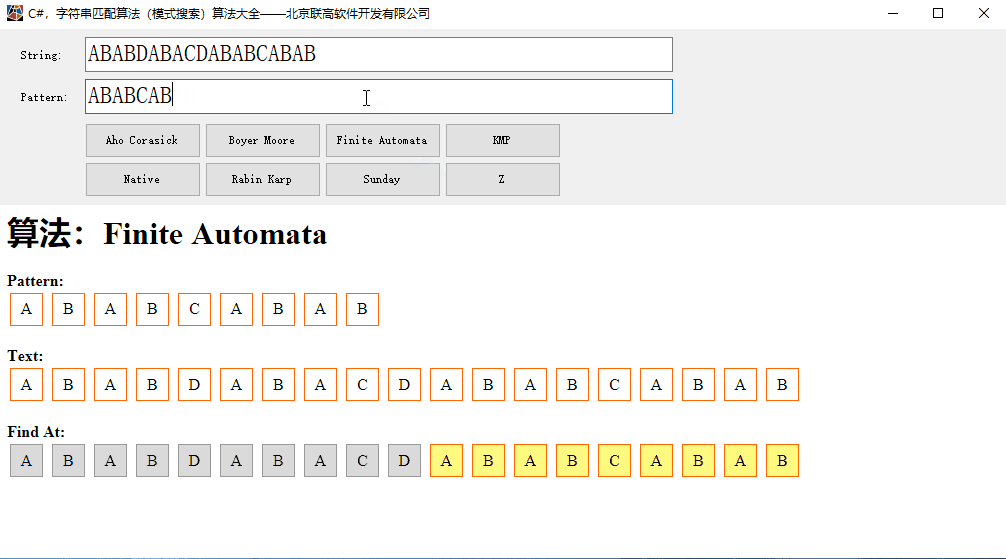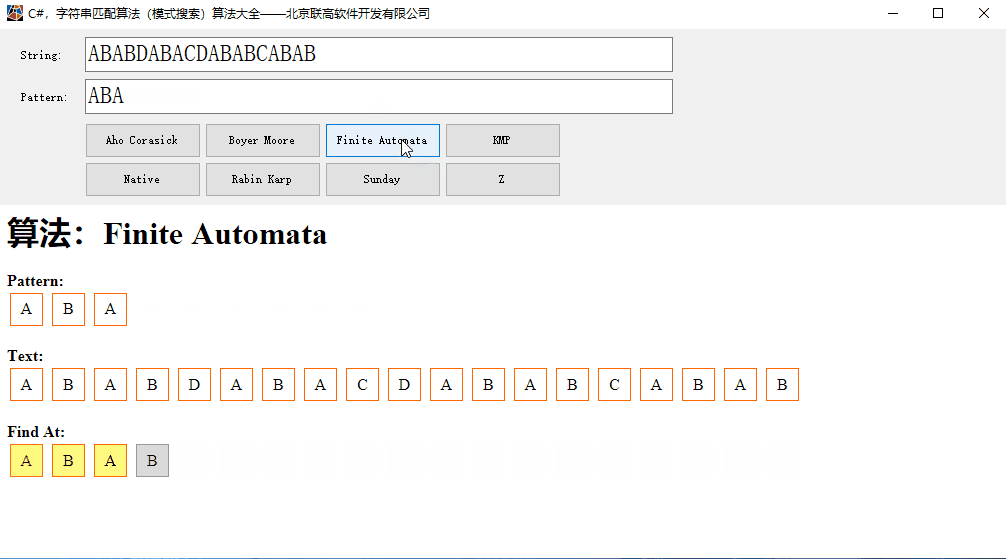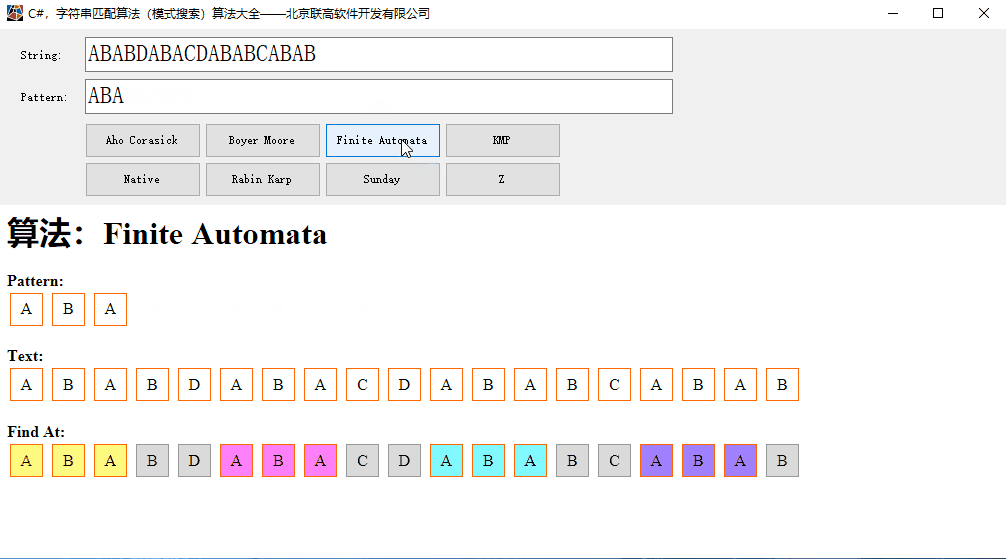
二、有限状态机用于字符串匹配(模式搜索)
假定要查找的字符串为P=”ABABCABAB”,被查找的文本为T=”ABABDABACDABABCABAB”。 一次读入T的一个字符,用S表示当前读入的T的字符,一开始读入一个字符,于是S=a。然后看看,从P开始,连续几个字符所构成的字符串可以成为S的后缀,由于当前S只有一个字符A,于是从P开始,连续1个字符所形成的字符串”A”,可以作为S的后缀。把这个字符串的长度记为k,于是此时k 等于1。继续从T中读入字符,于是S=”AB”, 此时,从P开始,连续两个字符所构成的字符串”AB”可以作为S的后缀,于是k = 2。如此反复。
利用有限状态机便可以构造这样的后缀序列。
源代码:
using System;
using System.Text;
using System.Collections;
using System.Collections.Generic;
namespace Legalsoft.Truffer.Algorithm
{
public static partial class PatternSearch
{
/// <summary>
/// 下一个状态
/// </summary>
/// <param name="patternArray"></param>
/// <param name="M"></param>
/// <param name="state"></param>
/// <param name="x"></param>
/// <returns></returns>
public static int NextState(char[] patternArray, int M, int state, int x)
{
if (state < M && (char)x == patternArray[state])
{
return state + 1;
}
for (int ns = state; ns > 0; ns--)
{
if (patternArray[ns - 1] == (char)x)
{
int i;
for (i = 0; i < ns - 1; i++)
{
if (patternArray[i] != patternArray[state - ns + 1 + i])
{
break;
}
}
if (i == ns - 1)
{
return ns;
}
}
}
return 0;
}
/// <summary>
/// 计算TF表
/// </summary>
/// <param name="patternArray"></param>
/// <param name="M"></param>
/// <returns></returns>
public static int[,] Compute_TF(char[] patternArray, int M)
{
int[,] TF = new int[M + 1, ALPHA_CODE_MAX];
for (int state = 0; state <= M; ++state)
{
for (int x = 0; x < ALPHA_CODE_MAX; ++x)
{
TF[state, x] = NextState(patternArray, M, state, x);
}
}
return TF;
}
/// <summary>
/// 字符串匹配算法(模式搜索)Finite Automata算法
/// </summary>
/// <param name="text"></param>
/// <param name="pattern"></param>
/// <returns></returns>
public static List<int> Finite_Automata_Search(string text, string pattern)
{
List<int> matchs = new List<int>();
int M = pattern.Length;
int N = text.Length;
int[,] TF = Compute_TF(pattern.ToCharArray(), M);//, TF);
int state = 0;
for (int i = 0; i < N; i++)
{
state = TF[state, text[i]];
if (state == M)
{
matchs.Add((i - M + 1));
}
}
return matchs;
}
}
}
-----------------------------------------------------------------------------
POWER BY TRUFFER.CN
using System;
using System.Text;
using System.Collections;
using System.Collections.Generic;
namespace Legalsoft.Truffer.Algorithm
{
public static partial class PatternSearch
{
/// <summary>
/// 下一个状态
/// </summary>
/// <param name="patternArray"></param>
/// <param name="M"></param>
/// <param name="state"></param>
/// <param name="x"></param>
/// <returns></returns>
public static int NextState(char[] patternArray, int M, int state, int x)
{
if (state < M && (char)x == patternArray[state])
{
return state + 1;
}
for (int ns = state; ns > 0; ns--)
{
if (patternArray[ns - 1] == (char)x)
{
int i;
for (i = 0; i < ns - 1; i++)
{
if (patternArray[i] != patternArray[state - ns + 1 + i])
{
break;
}
}
if (i == ns - 1)
{
return ns;
}
}
}
return 0;
}
/// <summary>
/// 计算TF表
/// </summary>
/// <param name="patternArray"></param>
/// <param name="M"></param>
/// <returns></returns>
public static int[,] Compute_TF(char[] patternArray, int M)
{
int[,] TF = new int[M + 1, ALPHA_CODE_MAX];
for (int state = 0; state <= M; ++state)
{
for (int x = 0; x < ALPHA_CODE_MAX; ++x)
{
TF[state, x] = NextState(patternArray, M, state, x);
}
}
return TF;
}
/// <summary>
/// 字符串匹配算法(模式搜索)Finite Automata算法
/// </summary>
/// <param name="text"></param>
/// <param name="pattern"></param>
/// <returns></returns>
public static List<int> Finite_Automata_Search(string text, string pattern)
{
List<int> matchs = new List<int>();
int M = pattern.Length;
int N = text.Length;
int[,] TF = Compute_TF(pattern.ToCharArray(), M);//, TF);
int state = 0;
for (int i = 0; i < N; i++)
{
state = TF[state, text[i]];
if (state == M)
{
matchs.Add((i - M + 1));
}
}
return matchs;
}
}
}