实验5-1 最短下降路径问题

【样例输入】
3
2 1 3
6 5 4
7 8 9
【样例输出】
13
#include<bits/stdc++.h>
using namespace std;
const int N = 105;
int n;
int g[N][N];
int f[N][N];
int res = 1e9+5;
int main()
{
cin>>n;
for(int i = 1; i <= n; i ++)
for(int j = 1; j <= n; j ++)
cin>>g[i][j];
for(int j = 1 ; j <= n; j++)
f[1][j] = g[1][j];
for(int i = 2 ; i <= n; i ++)
for(int j = 1 ; j <= n; j ++)
{
f[i][j] = f[i-1][j];
if(j-1>=1)f[i][j] = min(f[i][j],f[i-1][j-1]); //左面还有元素
if(j+1<=n)f[i][j] = min(f[i][j],f[i-1][j+1]); //右面还有元素
f[i][j] += g[i][j];
}
for(int i = 1 ; i <= n ; i ++)
res = min(res,f[n][i]);
cout<<res;
return 0;
}实验5-2 最少硬币问题—动态规划
| 最少硬币问题----动态规划 问题描述: 设有n 种不同面值的硬币,各硬币的面值存于数组T[1:n ]中。现要用这些面值的硬币来找钱。可以使用的各种面值的硬币个数存于数组Coins[1:n ]中。对任意钱数0≤m≤20001,设计一个用最少硬币找钱m 的方法。 编程任务: 对于给定的1≤n≤10,硬币面值数组T 和可以使用的各种面值的硬币个数数组Coins, 以及钱数m,0≤m≤20001,编程计算找钱m 的最少硬币数。 数据输入: 由文件input.txt 提供输入数据,文件的第一行中只有1 个整数给出n 的值,第2 行起每行2 个数,分别是T[j] 和Coins[j] 。最后1 行是要找的钱数m。 结果输出: 程序运行结束时,将计算出的最少硬币数输出到文件output.txt 中。问题无解时输出-1。 输入文件示例输出文件示例 input.txt output.txt 3 5 1 3 2 3 5 3 18 |
#include<bits/stdc++.h>
using namespace std;
const int N = 11;
int coin[N],num[N],f[20005];
//f[]存储到达各个金额所需的最少硬币数量
const int INF = 0x3f3f3f3f;
int main()
{
int n,m;
cin >> n;
for(int i=0;i<n;i++) cin >> coin[i] >> num[i];
cin >> m;
for(int i=1;i<=m;i++) f[i]=INF;
//核心代码
for(int i=0;i<n;i++) //遍历每种硬币
for(int j=1;j<=num[i];j++) //对于每种硬币,考虑从1到该硬币的数量
{
for(int k=m;k>=coin[i];k--) //从目标金额开始向下遍历到当前硬币面额。
{
f[k]=min(f[k],f[k-coin[i]]+1); //更新f[k],即组成金额k所需的最少硬币数量
}
}
//
cout << (f[m] < m ? f[m] : -1) ;
}实验5-3 独立任务最优调度问题
问题描述:
用2 台处理机A 和B 处理n 个作业。设第i 个作业交给机器A 处理时需要时间ai ,若由机器B 来处理,则需要时间bi。由于各作业的特点和机器的性能关系,很可能对于某些i, 有ai ≥ bi ,而对于某些j,j≠i,有aj < bj 。既不能将一个作业分开由2 台机器处理,也没有一台机器能同时处理2 个作业。设计一个动态规划算法,使得这2 台机器处理完这n 个作业的时间最短(从任何一台机器开工到最后一台机器停工的总时间)。研究一个实例:(a1,a2,a3,a4,a5,a6)=(2,5,7,10,5,2);(b1,b2,b3,b4,b5,b6)=(3,8,4,11,3,4) 。
编程任务:
对于给定的2 台处理机A 和B 处理n 个作业,找出一个最优调度方案,使2 台机器处理完这n 个作业的时间最短。
数据输入:
由文件input.txt 提供输入数据。文件的第1 行是1 个正整数n, 表示要处理n 个作业。接下来的2 行中,每行有n 个正整数,分别表示处理机A 和B 处理第i 个作业需要的处理时间。
结果输出:
程序运行结束时,将计算出的最短处理时间输出到文件output.txt 中。
输入文件示例输出文件示例
input.txt output.txt
6 15
2 5 7 10 5 2
3 8 4 11 3 4
#include<bits/stdc++.h>
using namespace std;
const int N = 1010;
int n, a[N], b[N];
int ans, sum, dp[N][N];
int main() {
cin >> n;
for (int i = 1; i <= n; i++) cin >> a[i], sum += a[i];
for (int i = 1; i <= n; i++) cin >> b[i];
memset(dp, 0x3f, sizeof(dp));
dp[0][0] = 0;
for (int i = 1; i <= n; i++) {
for (int j = 0; j <= sum; j++) {
if (j >= a[i]) {
//A B择优
dp[i][j] = min(dp[i - 1][j - a[i]], dp[i - 1][j] + b[i]);
} else {
//只能B机器做
dp[i][j] = dp[i - 1][j] + b[i];
}
}
}
//找出最小的值
ans = 0x3f3f3f3f;
for (int i = 0; i <= sum; i++) {
int t = max(i, dp[n][i]);
ans = min(ans, t);
}
cout << ans << endl;
return 0;
}实验5-4 双调旅行售货员问题—动态规划
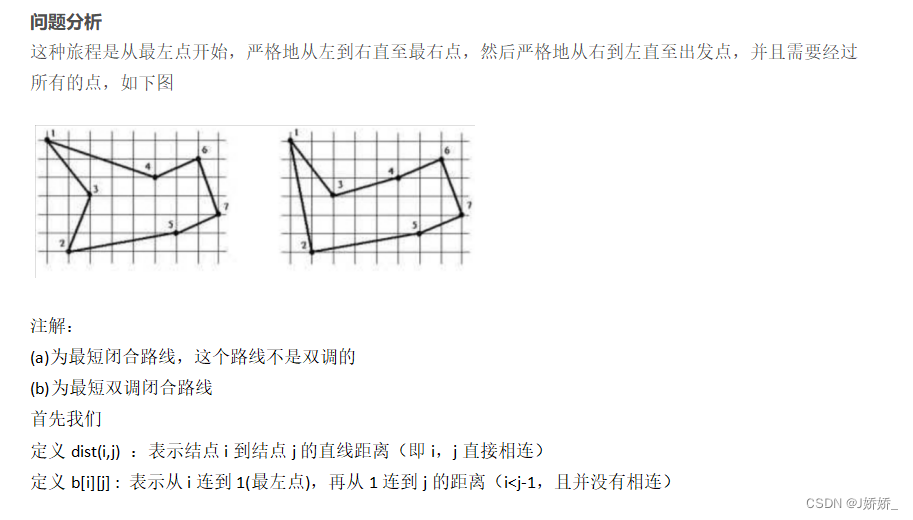
欧氏旅行售货员问题是对给定的平面上n 个点确定一条连接这n 个点的长度最短的哈密顿回路。由于欧氏距离满足三角不等式,所以欧氏旅行售货员问题是一个特殊的具有三角不等式性质的旅行售货员问题。它仍是一个NP 完全问题。最短双调TSP 回路是欧氏旅行售货员问题的特殊情况。平面上n 个点的双调TSP 回路是从最左点开始,严格地由左至右直到最右点,然后严格地由右至左直至最左点,且连接每一个点恰好一次的一条闭合回路。
编程任务:
给定平面上n 个点,编程计算这n 个点的最短双调TSP 回路。
数据输入:
由文件input.txt 给出输入数据。第1 行有1 个正整数n,表示给定的平面上的点数。接下来的n 行中,每行2 个实数,分别表示点的x 坐标和y 坐标。
结果输出:
将计算的最短双调TSP 回路的长度(保留2 位小数)输出到文件output.txt 。
输入文件示例 输出文件示例
input.txt output.txt
7 25.58
0 6
1 0
2 3
5 4
6 1
7 5
8 2
#include<bits/stdc++.h>
using namespace std;
const int maxn = 1010;
const double inf = 0x3f3f3f;
int n;
double x[maxn],y[maxn],dis[maxn][maxn],dp[maxn][maxn];
double cal(double x1,double x2,double y1,double y2)
{
return sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2));
}
void solve()
{
dp[1][2]=dis[1][2];
for(int j=3;j<=n;j++){
for(int i=1;i<=j-2;i++)dp[i][j]=dp[i][j-1]+dis[j-1][j];
double Min=inf;
for(int k=1;k<=j-2;k++)Min=min(Min,dp[k][j-1]+dis[k][j]);
dp[j-1][j]=Min;
}
dp[n][n]=dp[n-1][n]+dis[n-1][n];
printf("%.2lf\n",dp[n][n]);
}
int main()
{
cin >> n;
for(int i = 1 ; i <= n ; i ++ )
cin >> x[i] >> y[i];
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
dis[i][j]=cal(x[i],x[j],y[i],y[j]);
solve();
return 0;
}