学习笔记-李沐动手学深度学习（一）（01-07）

个人随笔

第三列是 jupyter记事本
在这里插入图片描述
官方github上啥都有（代码、jupyter记事本、胶片）
https://github.com/d2l-ai

多体会

【梯度指向的是值变化最大的方向】

符号

在这里插入图片描述

维度

（弹幕说）2，3，4越后面维度越低 4就是一维有4个标量
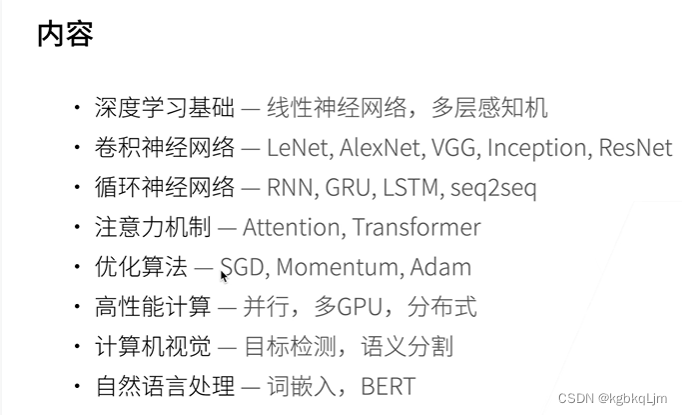
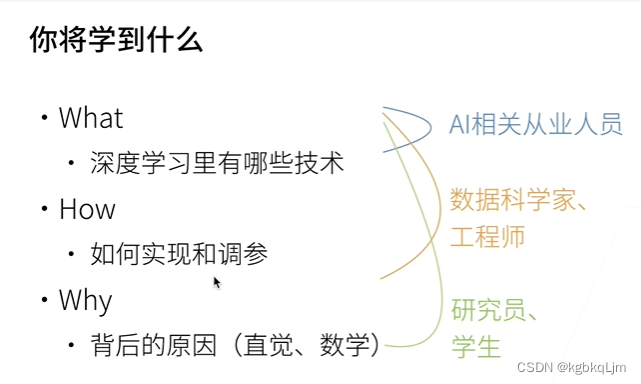
在这里插入图片描述

00-预告

在这里插入图片描述

01-课程安排

在这里插入图片描述

02-深度学习介绍

【语言是一个符号】
【深度学习是机器学习的一种】
最热的方向：深度学习和CV、NLP结合

【AI地图】
① 如下图所示，X轴是不同的模式，最早的是符号学，然后概率模型、机器学习。Y轴是我们想做什么东西，感知是我了解这是什么东西，推理形成自己的知识，然后做规划。
② 感知类似我能看到前面有个屏幕，推理是基于我看到的东西想象未来会发生什么事，根据看到的现象、数据，形成自己的知识，知道所有知识后能进行长远的规划，未来怎么做

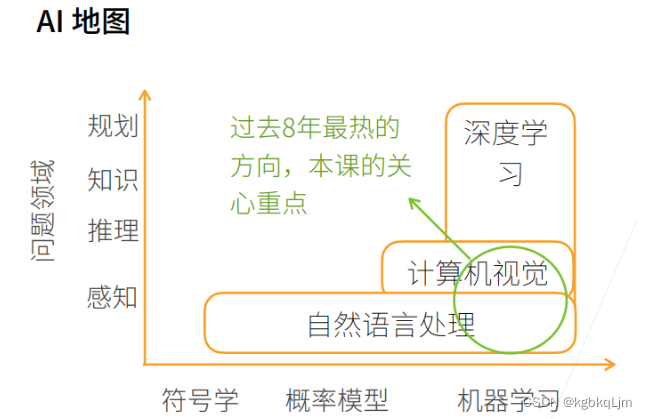
在这里插入图片描述

① 自然语言处理目前还是停留在感知上，人几秒钟能反应过来的东西都属于感知范围，即使像中文翻译成英文，英文翻译成中文那种。
② 计算机视觉可以在图片里面可以做一些推理。
③ 自然语言处理里面有符号，所以有符号学，并且还可以用概率模型、机器学习。计算机视觉面对的是图片，图片里面都是一个个像素，像素很难用符号学来解释，所以计算机视觉大部分用概率模型、机器学习来解释。
④ 深度学习是计算机视觉中的一种方法，它还有其他应用方法。

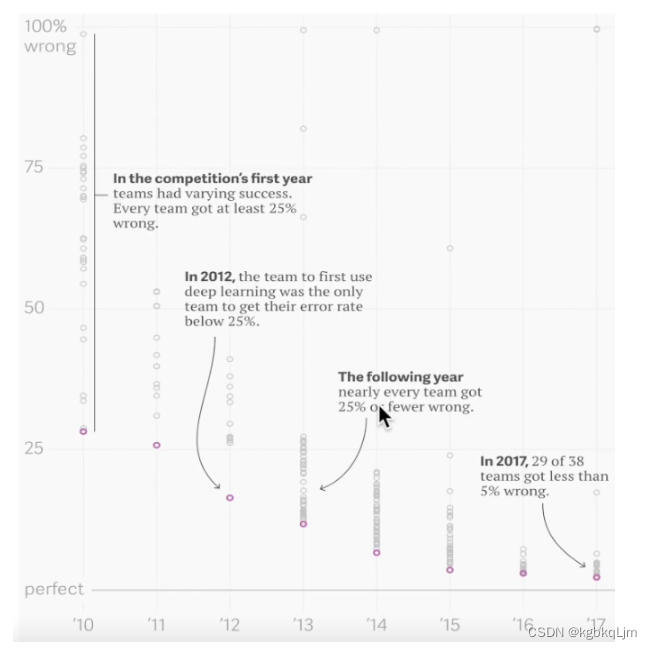
图片分类

在这里插入图片描述

① 可以看到从12年开始，图片分类错误率开始有一个比较大的下降，12年就是深度学习引入图片分类的开始。

② 17年的时候，几乎所有的团队都可以做到5%以内的错误率，基本上可以达到人类在图片识别上的精度了。可以说在图片分类上，深度学习已经做的很好了
在这里插入图片描述

物体检测和分割

① 知道图片是内容，在什么地方，这就是物体检测。

② 物体分割是指每个像素它到底是飞机还是人。

在这里插入图片描述

样式迁移

相当于滤镜
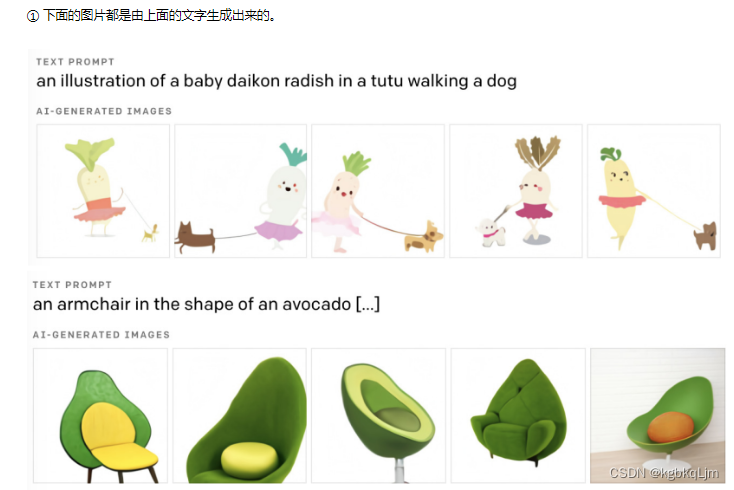
在这里插入图片描述

人脸合成

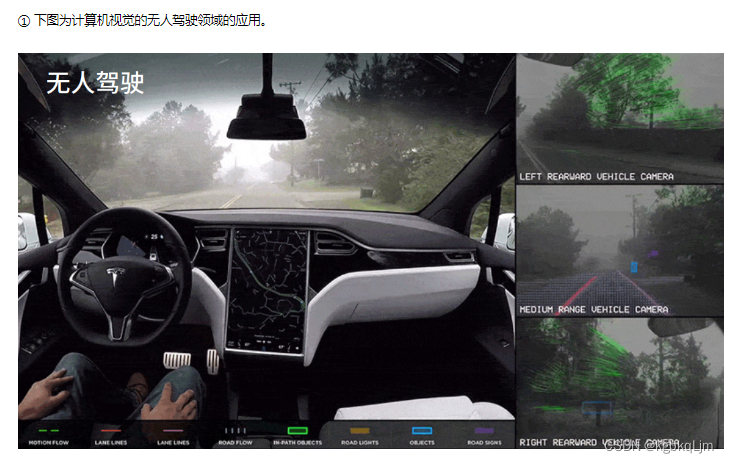
在这里插入图片描述

文字生成图片

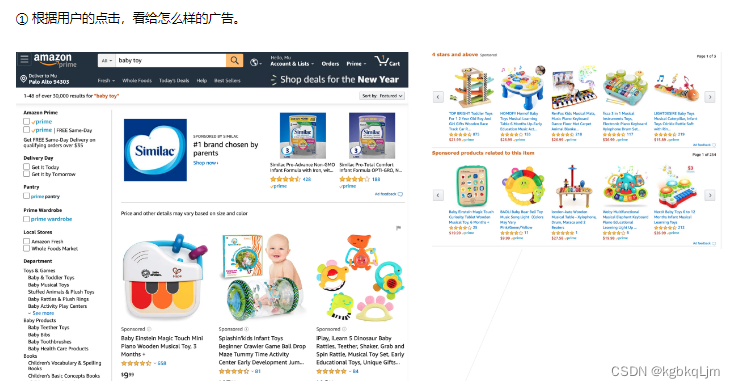
在这里插入图片描述

文字生成

在这里插入图片描述

无人驾驶

在这里插入图片描述

【案例】广告点击

在这里插入图片描述
p是用户点击的概率

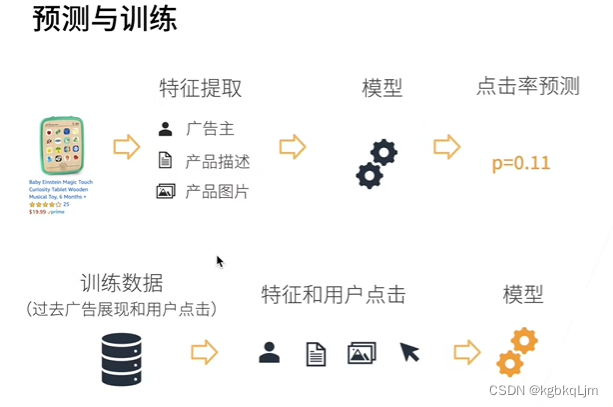
【完整的故事】

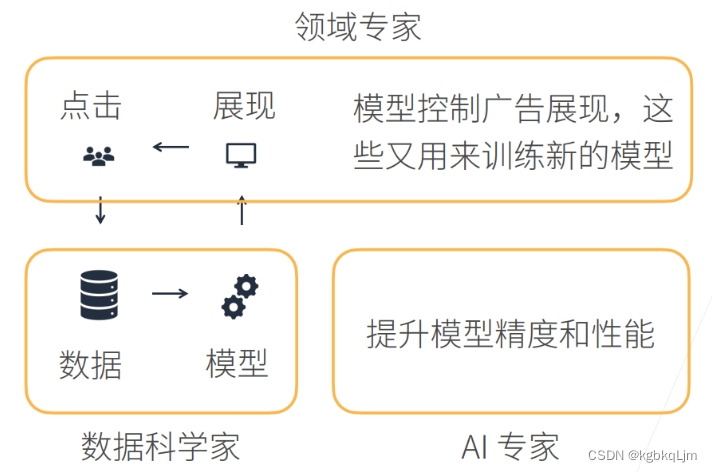
在这里插入图片描述

QA

有效和可解释性是不同的

有效应该是简单的解释一下
可解释性更深入

领域专家：甲方、产品经历、提业务需求的人，了解业务的人
数据科学家：乙方，实现需求的人，搬砖工程师（偏广）
AI专家：资深数据科学家，不仅能实现还要提高精度（偏深）

如何找论文？后续会讲

03-安装（CPU，后续将GPU）

d2l：Diving Into Deep Learning动手学深度学习的缩写
在这里插入图片描述

conda env remove d2l-zh
conda create -n d2l-zh -y python=3.8 pip
conda activate d2l-zh

pip install -y jupyter d2l torch torchvision

wget https://zh-v2.d2l.ai/d2l-zh.zip
unzip d2l-zh.zip
jupyter notebook

弹幕说：这个create -n -y d2l啥的不行啊，改成create -n d2l -y可以用了

老师操作（感觉本地配环境，这部分全都可以跳过）

视频中老师演示的是在亚马逊云上创建的云环境ubuntu18.04，并且刚拿到机器后装了一些基本的内容：miniconda（具体在linux系统下安装时再看吧）

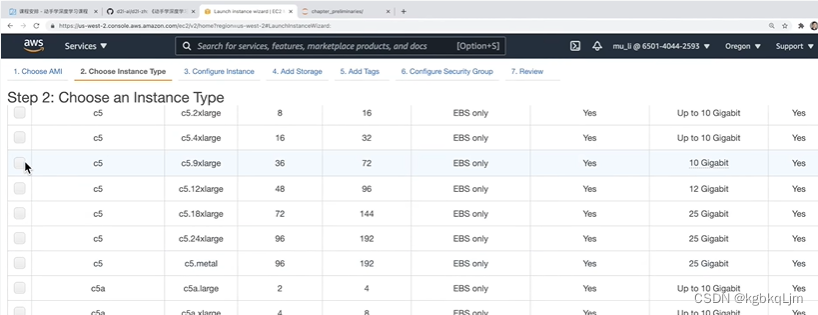
在这里插入图片描述
本地连接远程机器：

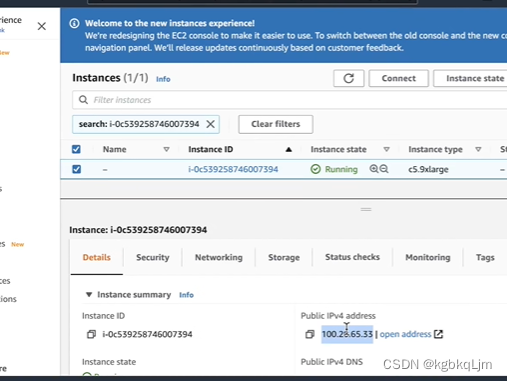
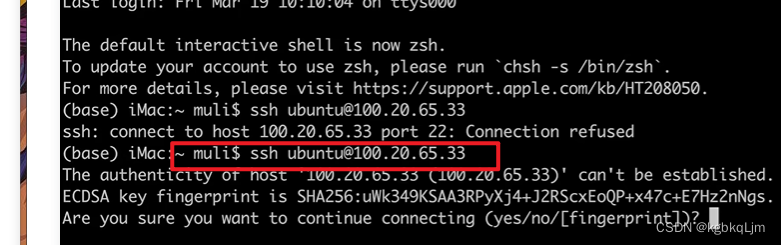
此时连接成功，后面有很多细节，安装基本东西来着：（apt是一种linux的包管理软件）
sudo apt update更新机器
sudo apt install build-essential
sudo apt install python3.8
安装miniconda，复制官网链接，本地wget+链接安装：（是什么系统就装什么）
在这里插入图片描述

bash本地安装miniconda：

yes

此时就安装到机器的根目录下，然后bash后就进入了conda环境

此时可以在conda环境上安装各种需要的包

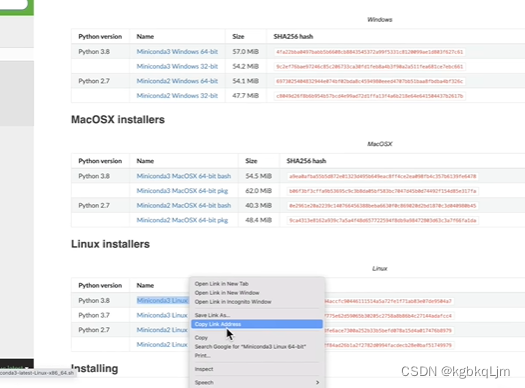
老师基于【wget 下载地址链接】即可下载下来，下载地址链接是到了安装包链接后右键copy如下图
在这里插入图片描述

然后自己装unzip并解压

在这里插入图片描述
视频用的pytorch版本

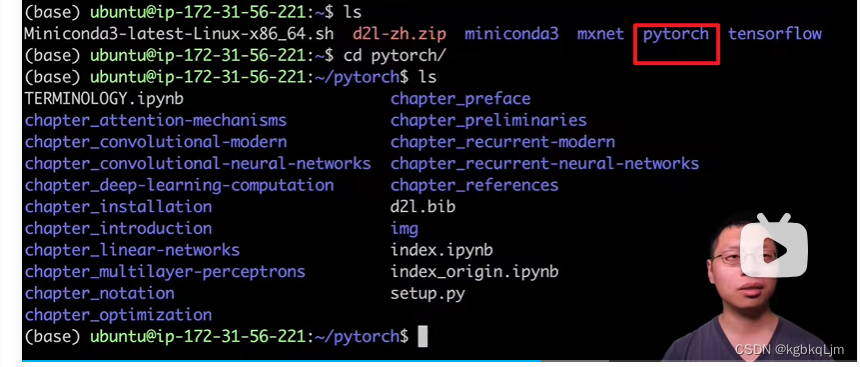
老师后面将远端地址（因为是本地ssh远程连接到了亚马逊云上的一台ubuntu18.04）映射到了本地机器

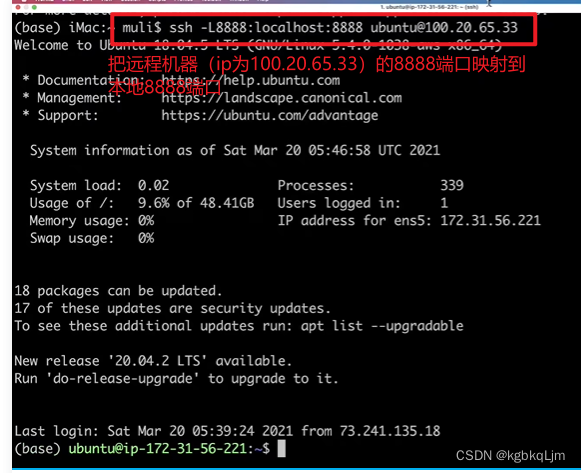
此时可以启动jupyter后直接访问刚刚下载的课程的jupyter
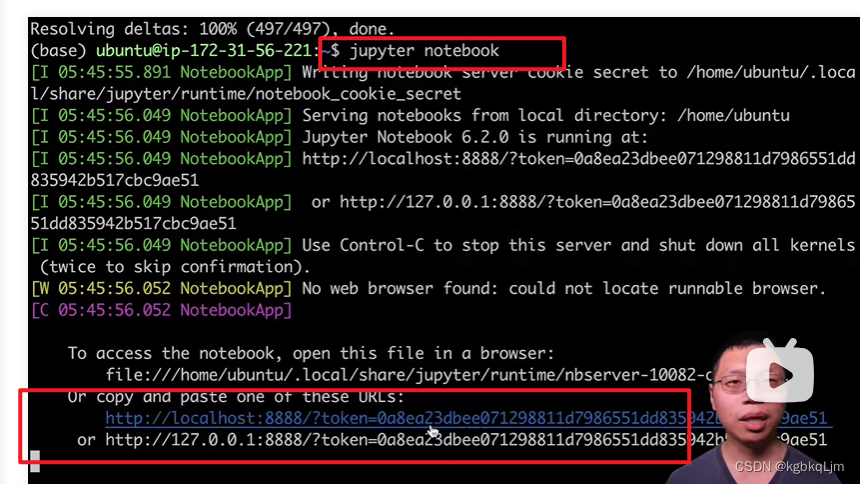
在这里插入图片描述

在这里插入图片描述
看到刚刚装的东西

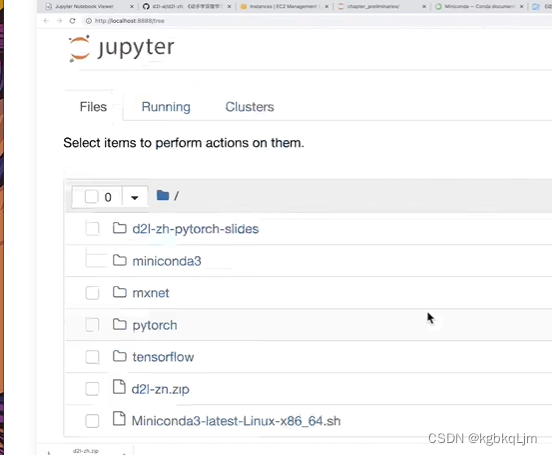
本地实操

【实操】用conda创建一个python=3.8名为ljm-d2l-learn的虚拟环境
conda create -n ljm-d2l-leran -y python=3.8
conda env list查看环境
conda activate ljm-d2l-learn进行环境
pip install jupyter d2l torch torchvision安装（开梯子巨快）

pip install rise安装rise插件，这样可以以幻灯片方式查看 jupyter记事本中的课件
rise安装前，显示jupyter中幻灯片内容的效果：
在这里插入图片描述
rise安装后：
刷新页面后点击这个

以幻灯片形式展示：

自己测试了一下，在base环境上就能显示该按钮

04-数据操作+数据预处理

N维数组

① 机器学习用的最多的是N维数组，N维数组是机器学习和神经网络的主要数据结构。

笔记中所提到的x维tensor和x维数组是一回事

0维：标量（即一个数字）
1维：向量
2维：矩阵（每一行是一个样本，每一列是不同样本的相同种特征）
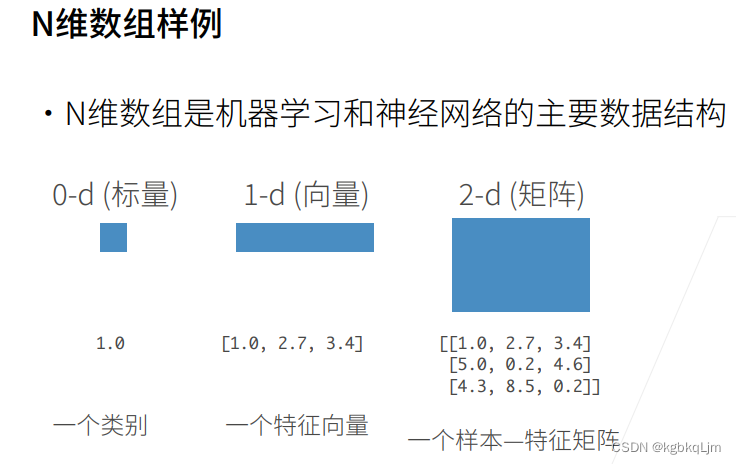
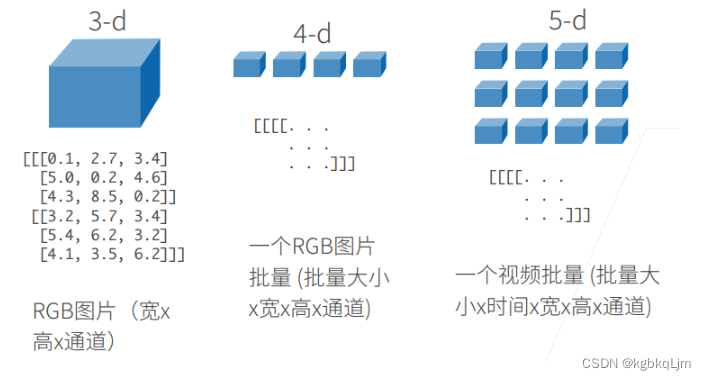
在这里插入图片描述
3维：如图片
4维：n个三维数组放在一起，如一个RGB图片的批量，一个batch
5维：如视频的批量（多了一个时间的维度）

创建数组

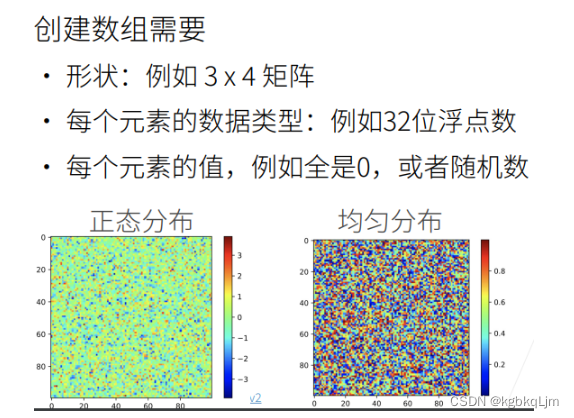
① 创建数组需要：形状、指定每个元素的数据类型、元素值。
如下图表示所有元素的值是按照正态分布表示的，右图指元素值可以按均匀分布来产生
在这里插入图片描述

访问元素

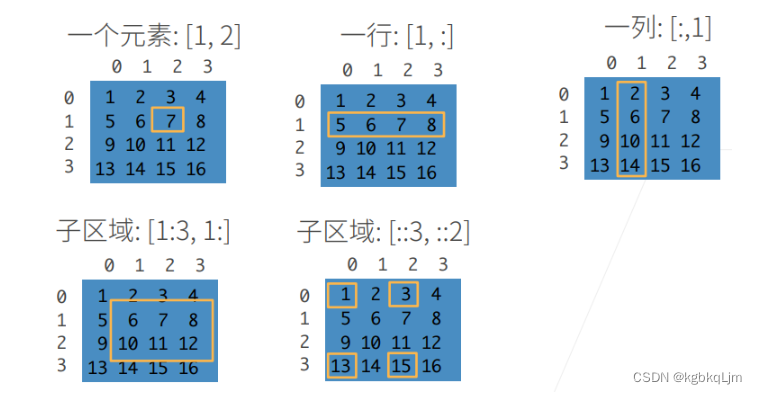
① 可以根据切片，或者间隔步长访问元素。
② [::3,::2]是每隔3行、2列访问。

注：索引都是从0开始
1.访问第一行第二列的元素
2.访问第一行所有元素
3.访问第一列所有元素
4.访问第一至三行（左闭右开，即第一、二行，不含第三行）的第一列及之后的所有元素
5.跳着访问：每隔3行、每个两列取一个元素
在这里插入图片描述

张量（tensor）数据操作

多体会

1.看打印出的tensor中括号数量来判断tensor（或者说数组）是几维的

二维数组：
含三个一维数组的二维数组
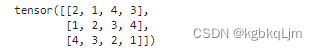
在这里插入图片描述

三维数组：
含一个二维数组的三维数组
在这里插入图片描述
含两个二维数组的三维数组

2.打印出来的torch.Size()中的一维数组中有几个元素就是几维数组

在这里插入图片描述

个人补充-为什么需要张量？张量的意义？

1.支持基于GPU加速（numpy型数据不支持）
2.支持自动求导（自动微分）（即计算梯度）
3.tensor类型数据变换更灵活多样
（土堆）包装了神经网络所需的理论基础参数的数据类型
在这里插入图片描述

【开源博主完整代码】

# 查看pytorch中的所有函数名或属性名
import torch

print(dir(torch.distributions))

print('1.张量的创建')
# ones 函数创建一个具有指定形状的新张量，并将所有元素值设置为 1
t = torch.ones(4)
print('t:', t)

x = torch.arange(12)
print('x:', x)
print('x shape:', x.shape)  # 访问向量的形状

y = x.reshape(3, 4)  # 改变一个张量的形状而不改变元素数量和元素值
print('y:', y)
print('y.numel():', y.numel())  # 返回张量中元素的总个数

z = torch.zeros(2, 3, 4)  # 创建一个张量，其中所有元素都设置为0
print('z:', z)

w = torch.randn(2, 3, 4)  # 每个元素都从均值为0、标准差为1的标准高斯（正态）分布中随机采样。
print('w:', w)

q = torch.tensor([[1, 2, 3], [4, 3, 2], [7, 4, 3]])  # 通过提供包含数值的 Python 列表（或嵌套列表）来为所需张量中的每个元素赋予确定值
print('q:', q)

print('2.张量的运算')
x = torch.tensor([1.0, 2, 4, 8])
y = torch.tensor([2, 2, 2, 2])
print(x + y)
print(x - y)
print(x * y)
print(x / y)
print(x ** y)  # **运算符是求幂运算
print(torch.exp(x))

X = torch.arange(12, dtype=torch.float32).reshape(3, 4)
Y = torch.tensor([[2.0, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])
print('cat操作 dim=0', torch.cat((X, Y), dim=0))
print('cat操作 dim=1', torch.cat((X, Y), dim=1))  # 连结（concatenate） ,将它们端到端堆叠以形成更大的张量。

print('X == Y', X == Y)  # 通过 逻辑运算符 构建二元张量
print('X < Y', X < Y)
print('张量所有元素的和:', X.sum())  # 张量所有元素的和

print('3.广播机制')
a = torch.arange(3).reshape(3, 1)
b = torch.arange(2).reshape(1, 2)
print('a:', a)
print('b:', b)
print('a + b:', a + b)  # 神奇的广播运算

print('4.索引和切片')
X = torch.arange(12, dtype=torch.float32).reshape(3, 4)
print('X:', X)
print('X[-1]:', X[-1])  # 用 [-1] 选择最后一个元素
print('X[1:3]:', X[1:3])  # 用 [1:3] 选择第二个和第三个元素]

X[1, 2] = 9  # 写入元素。
print('X:', X)

X[0:2, :] = 12  # 写入元素。
print('X:', X)

print('5.节约内存')
before = id(Y)  # id()函数提供了内存中引用对象的确切地址
Y = Y + X
print(id(Y) == before)

before = id(X)
X += Y
print(id(X) == before)  # 使用 X[:] = X + Y 或 X += Y 来减少操作的内存开销。

before = id(X)
X[:] = X + Y
print(id(X) == before)  # 使用 X[:] = X + Y 或 X += Y 来减少操作的内存开销。

print('6.转换为其他 Python对象')
Y = torch.tensor([[2.0, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])
A = Y.numpy()
print(type(A))  # 打印A的类型
print(A)
B = torch.tensor(A)
print(type(B))  # 打印B的类型
print(B)

a = torch.tensor([3.5])
print(a, a.item(), float(a), int(a))

导入torch库

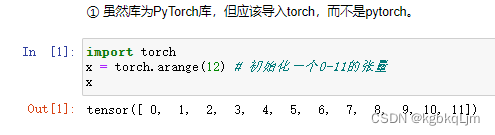
在这里插入图片描述

访问张量形状shape和元素总数numel

张量表示由一个数值组成的数组，这个数组可能有多个维度

x = torch.arange(12)：初始化[0, 12) 左闭右开区间上的所有数字为一个一维向量
在这里插入图片描述

x.shape
输出torch.Size([12])：说明这是一个一维向量，该向量的长度为12

numel：number of element，张量中元素的总数，是一个标量（数值）
在这里插入图片描述

直接生成一个形状为 3,4的元素为 0-11的向量

改变张量形状reshape

x = x.reshape(3,4) # 一维张量改为3行四列的张量
在这里插入图片描述

创建全0、全1张量

y = torch.zeros((2,3,4))：创建形状为 (2,3,4)的全0 张量（即2个3行4列的二维数组组成的三维数组）
在这里插入图片描述

创建特定值张量

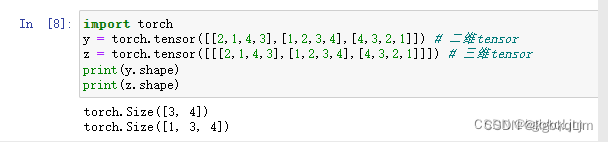
y = torch.tensor([[2,1,4,3],[1,2,3,4],[4,3,2,1]]) ：告诉torch 要创建的二维tensor（个人感觉的tips：因为有两个[ [）的
第一行元素是 [2,1,4,3]
第二行元素是[1,2,3,4]
第三行元素是[4,3,2,1]

z = torch.tensor([[[2,1,4,3],[1,2,3,4],[4,3,2,1]]])：同理三个 [ [ [ 就变成三维tensor
print(z.shape)
torch.Size([1, 3, 4]) ：一个由一个三行四列的二维数组组成的三维tensor（或称数组）（或者说有一个三维数组，其中有一个元素，该元素是一个三行四列的二维数组）
【个人总结】打印出来的torch.Size()中的一维数组中有几个元素就是几维数组
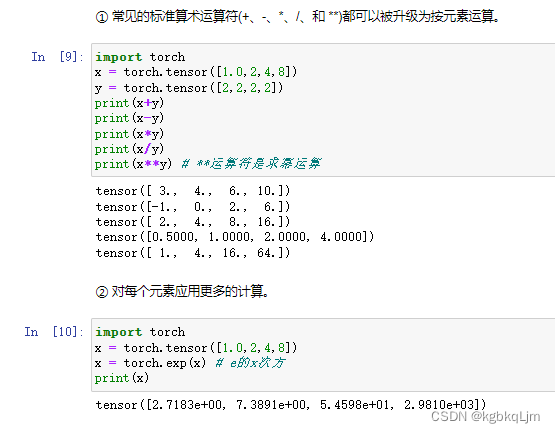
在这里插入图片描述

张量运算操作

所有的运算都是按元素进行的

x = torch.tensor([1.0,2,4,8]) ：创建一个元素类型都是浮点型的数组
x = torch.tensor([1,2,4,8])：创建一个元素类型都是整型的数组
在这里插入图片描述

张量合并操作(torch.cat)

cat>合并两个数组，dim.在第几维上进行合并

x = torch.arange(12,dtype=torch.float32).reshape((3,4))
y = torch.tensor([[2.0,1,4,3],[1,2,3,4],[4,3,2,1]])
m = torch.cat((x,y),dim=0) # 按第0个维度（对于二维数组来说，0就是行）合并起来
n = torch.cat((x,y),dim=1) # 按第一个维度（对于二维数组来说，1就是列）合并起来
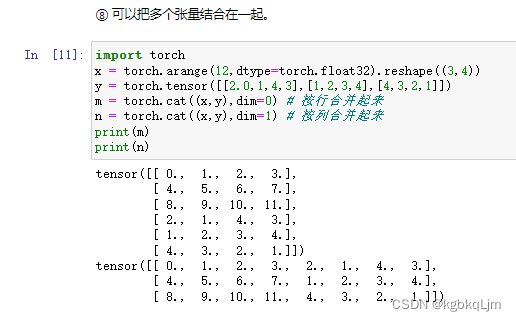
在这里插入图片描述
弹幕说：个人理解，dim=0 添加记录，dim=1拼接特征
dim＝几，就在第几个中括号内合并
0，1用作方向的表示方法在pytorch和numpy中有很多
0 和 1 这种表示法与 .shape的结果是对应的，0代表沿着第0个维度，1代表沿着第1个维度

张量逻辑运算（根据逻辑运算符构建二元张量）

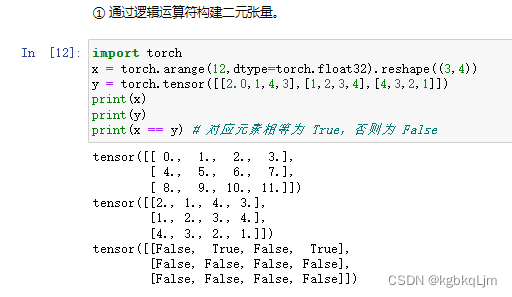
在这里插入图片描述

张量累加运算(.sum())

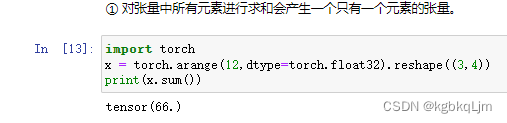
在这里插入图片描述

张量广播运算

前提是需要两个tensor的维度相同，形状可以不同（在新版本的python和torch中好像条件放宽了，可能是和numpy中广播的要求一致，具体用到再看）
注意：numpy中的广播和pytorch中的广播的要求好像在不同的python版本中有不同？torch中要求广播运算的两个tensor维度必须相同、形状可不同（好像对于新版本的python和pytorch的广播要求和numpy的一致了，具体用到再看）；numpy中在某些维度不同的数组之间也能进行广播
在这里插入图片描述

numpy中的广播

广播原则（broadcast）（尤其是形状不同的两个数组进行计算时）
广播：一个人说话，大家都能听见

【个人总结】从数组的形状的后面向前数，
tips：对于二维数组，如果二者的行形状相同或列形状相同，就可以计算

形状为(3,3,2)和(3,3)的数组不能运算
形状为(3,3,2)和(3,2)的数组可以运算
(4,1）和(4,6)可以
（1，6）和（4，6）可以

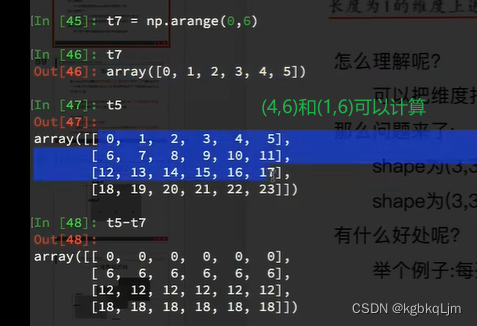
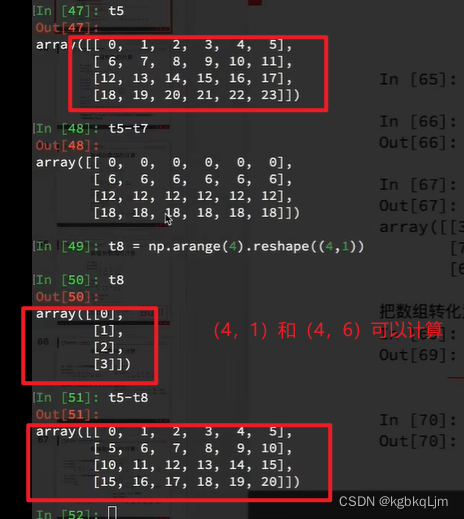
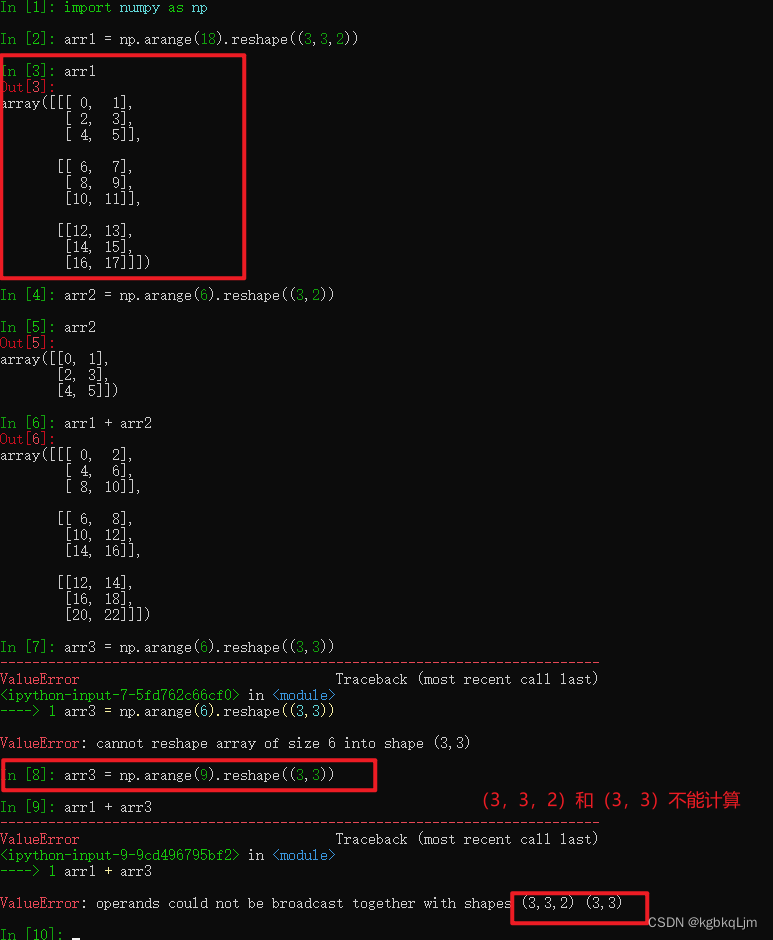
在这里插入图片描述

张量访问运算

x[-1]:访问最后一行
x[1:3]：访问第1、2行
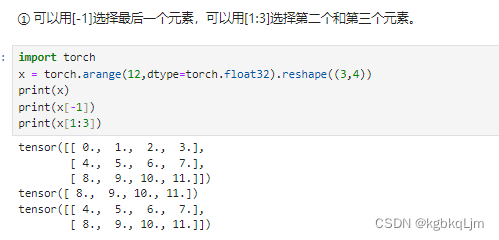
在这里插入图片描述

张量元素改写

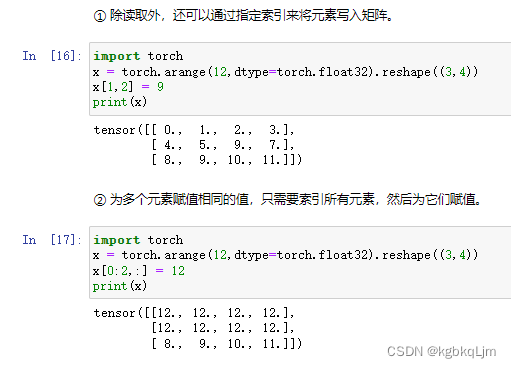
在这里插入图片描述

张量内存变化

id：类似于C++中的指针（相当于一个变量的唯一标识号）
如下图中：之前的变量y相当于被析构掉了（新的变量Y的id不等于以前的）
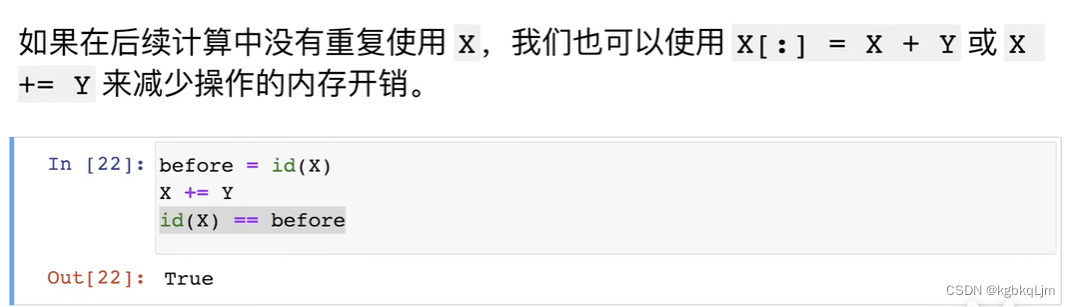
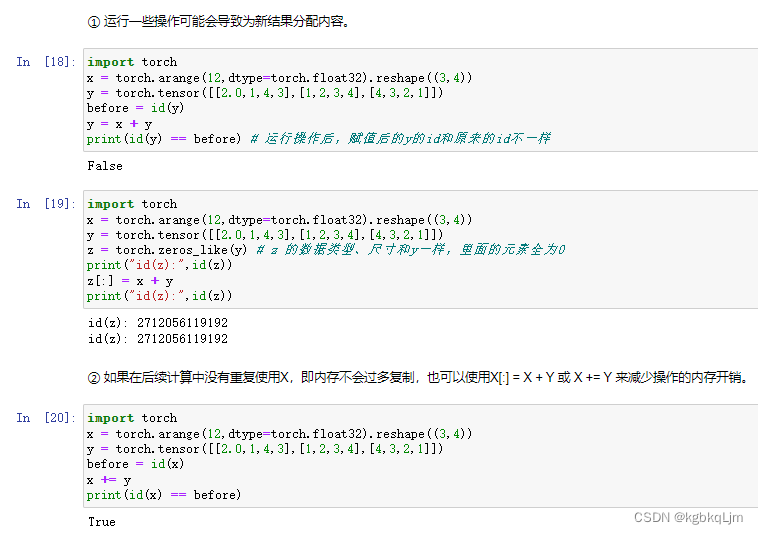
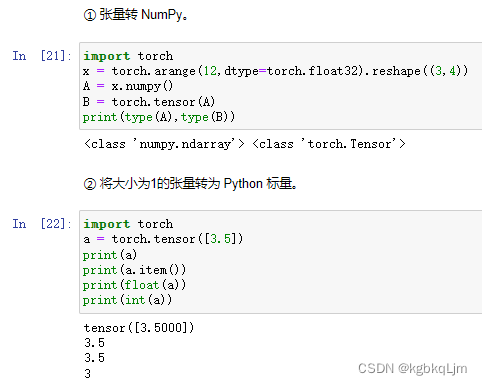
在这里插入图片描述

在这里插入图片描述

tensor和Numpy互转

在这里插入图片描述

数据预处理

csv全称“Comma-Separated Values”

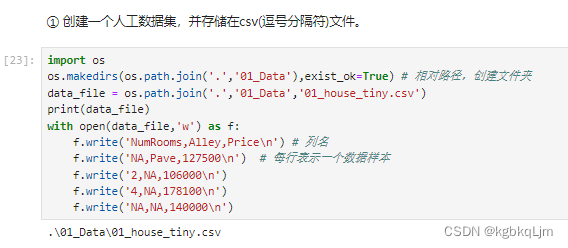
创建数据集

csv文件中的每列含义：房子有多少房间，进门的路是什么样的，房子的价格
NA：未知的
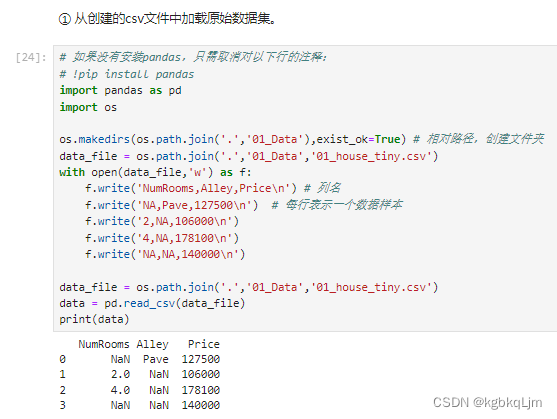
在这里插入图片描述

加载数据集

在这里插入图片描述

【举例】读取一个csv文件并预处理为pytorch中的tensor（含pandas基本操作）

iloc：index location

遇到Na数据：通常可以丢掉，但是太可惜了。因此常用的是插值法（如本例中，将原来是NaN的数据填成剩下的元素的均值，如2和4的均值是3）
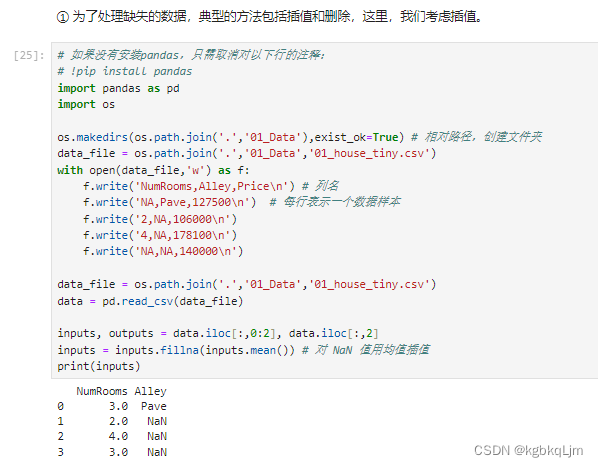
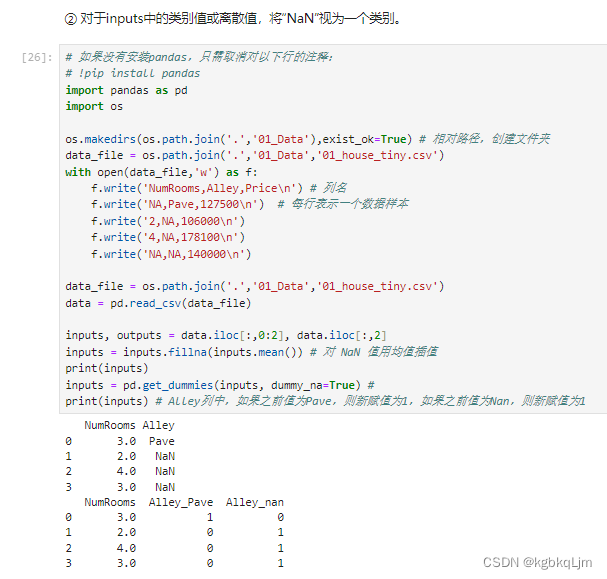
在这里插入图片描述

【过程】
1.原数据:

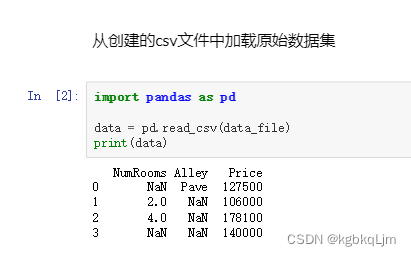
处理：
2.对于数值类型数据：拿到输入和输出数据，并将输入数据中（是数字类型的数据）缺失值NaN填为剩下的数据的均值

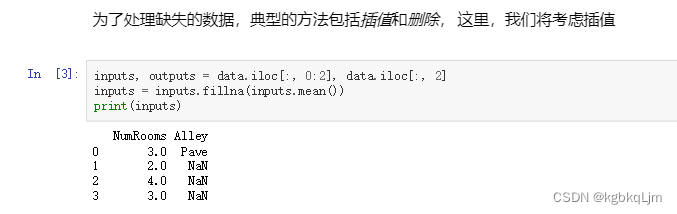
3.对于非数值类型数据：
方法一是将所有NaN的非数值数据单独做成一个特别的类（化为one-hot）
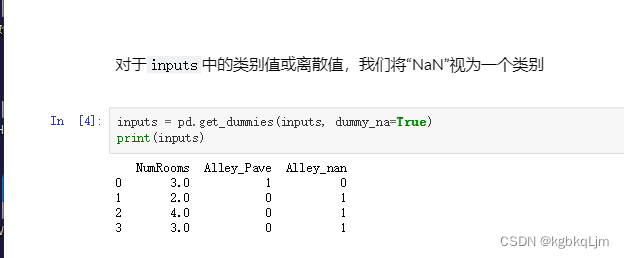
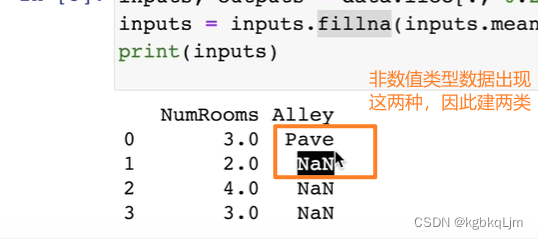
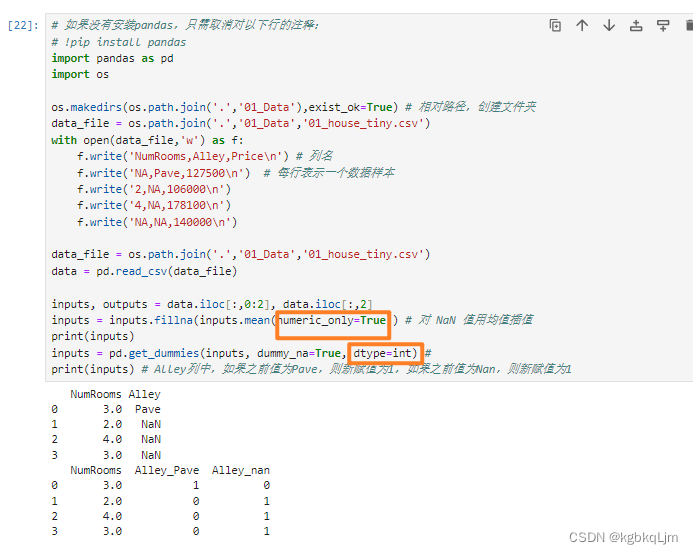
在这里插入图片描述

4.现在我们已经将所有的缺失值NaN和字符串都变成了数值，此时就可以将数据变为pytorch的tensor了
如下

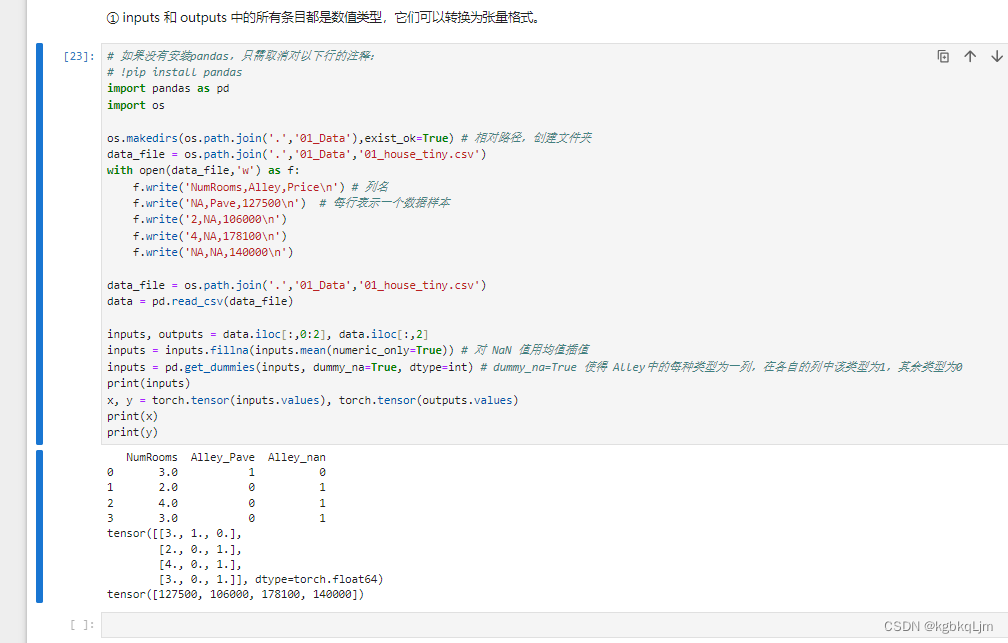
QA

1.view和reshape的区别：

弹幕说：数据库里面的View是视图，视图的作用就是提供更为便利的方式去操作数据。
如下图举个例子（实际这种情况很少见）
改b就相当于直接把a改了
在这里插入图片描述

3.如何看维度：
.shape()
.dim()方法
（弹幕说）2，3，4越后面维度越低 4就是一维有4个标量
在这里插入图片描述

4.pytorch的tensor和numpy的ndarray类似吗？
不类似

5.tensor和array的区别：
tensor是数学上的概念，ndarray是 n dimensionarray
array是计算机中的概念
但我们是混着用的，类似的
（弹幕说）传统张量在力学里面用的挺多，和深度学习的张量确实不是一个东西感觉~

6.有图形化的torch编程方案吗
暂无

7.内存？
python一般会自动释放

9.view和reshape没有本质区别
弹幕说：建議reshape，view報錯的可能情況更多

05-线性代数

理论

在这里插入图片描述
标量：

向量：

矩阵：

在这里插入图片描述

在这里插入图片描述
矩阵的范数：

正交矩阵：

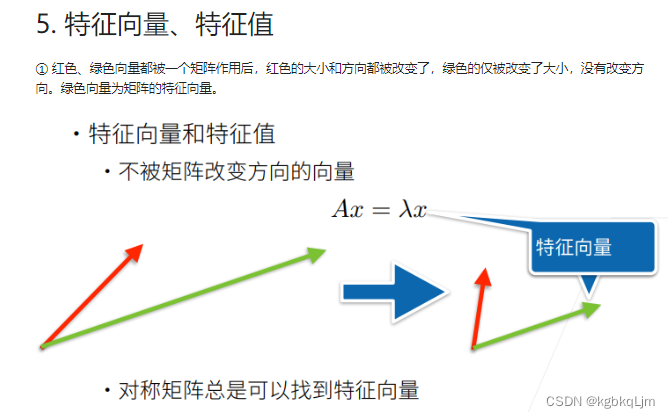
特征向量和特征值：

代码实现

标量、向量（创建和访问向量元素）

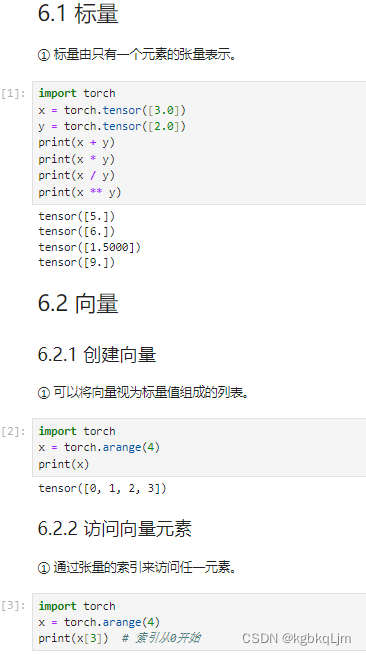
在这里插入图片描述

向量长度、向量维度、创建矩阵

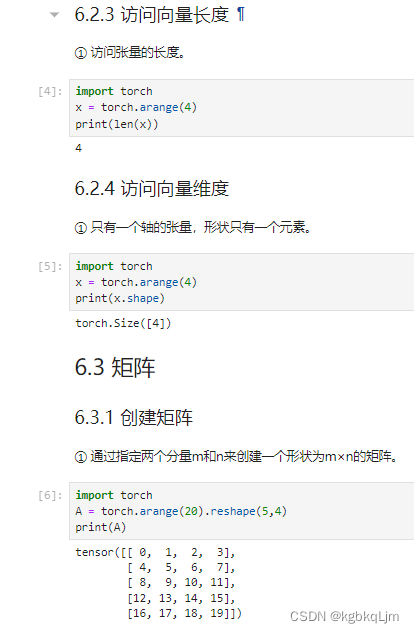
在这里插入图片描述

矩阵转置、对称矩阵

在这里插入图片描述

多维矩阵、矩阵克隆

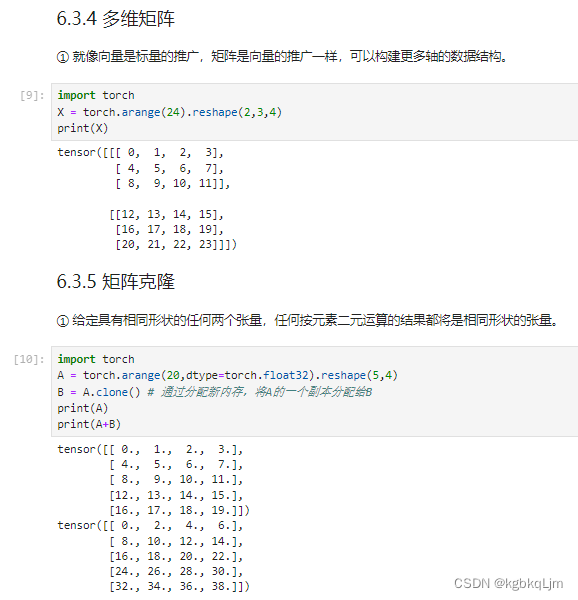
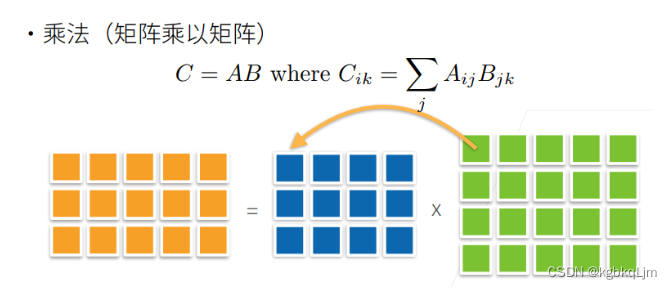
在这里插入图片描述

矩阵相乘、矩阵加标量

哈达玛积（矩阵按元素乘法）
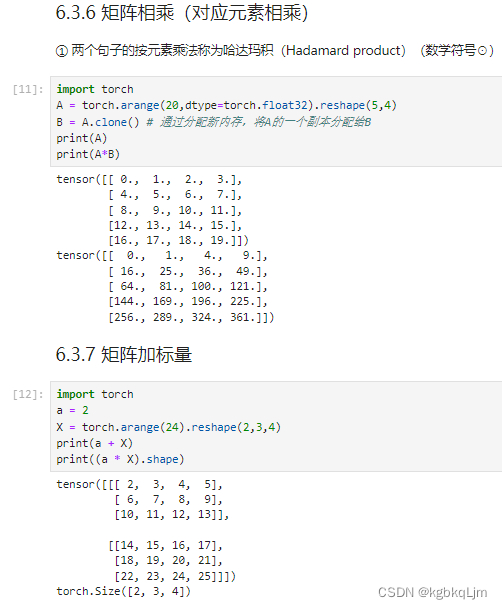
在这里插入图片描述

向量求和、矩阵求和

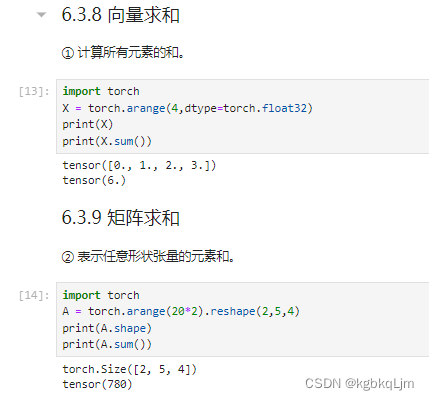
在这里插入图片描述

矩阵按某轴求和（计算后丢掉维度）、矩阵平均值mean

按哪个轴求和

弹幕说：
对哪个维度求和，就把哪个维度的数值变为1，比如第0个维度是2，对该维度求和就是把该维度变为1，即将该维度的数加在一起，再比如第一个维度是5（行），就把相同列的5行的数加起来，即把这个维度变为1
对哪个维度求和，最终发生改变的就是哪个维度，即该维度消失
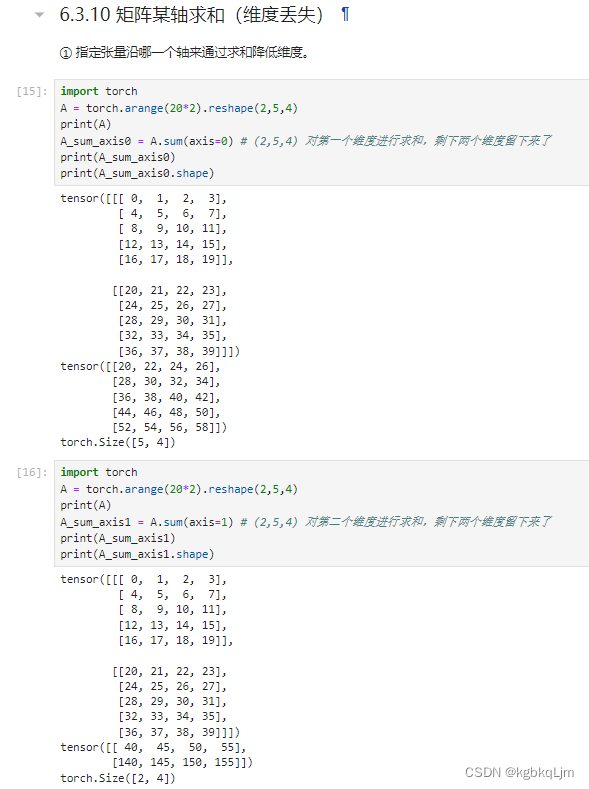
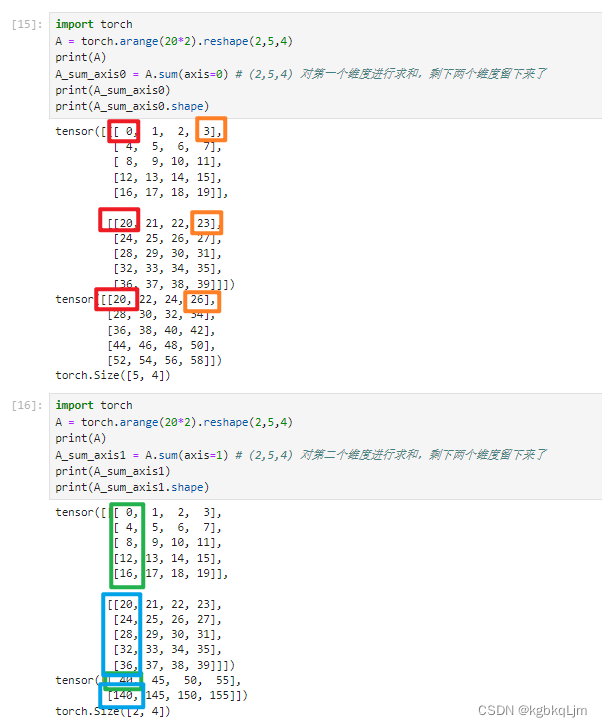
在这里插入图片描述

两个维度求和：个人理解即先对第一个维度求和，再对第二个维度求和

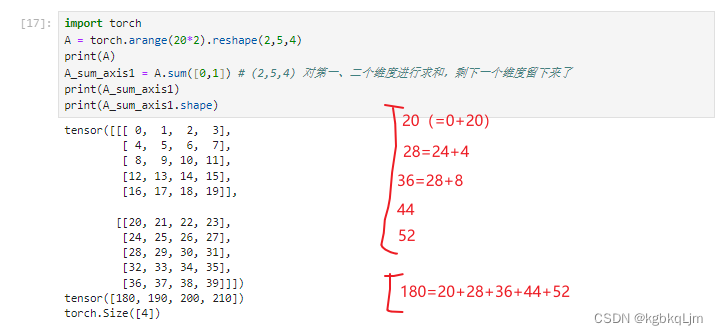
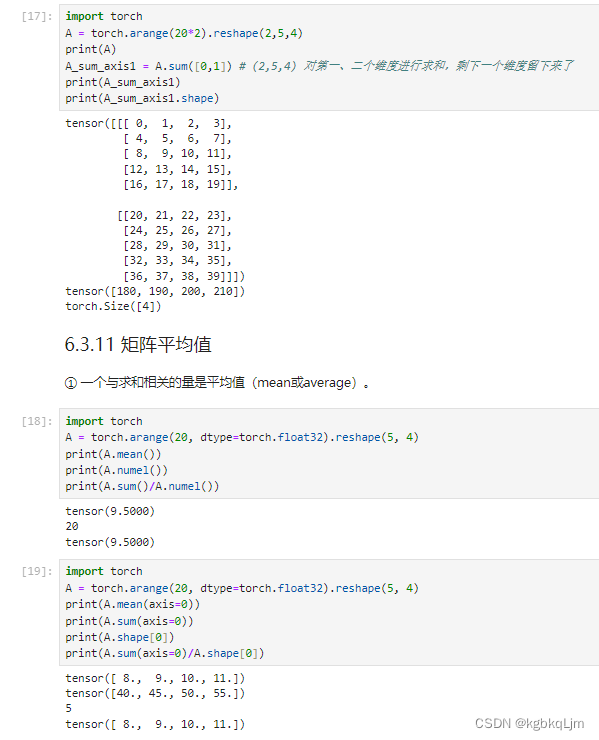
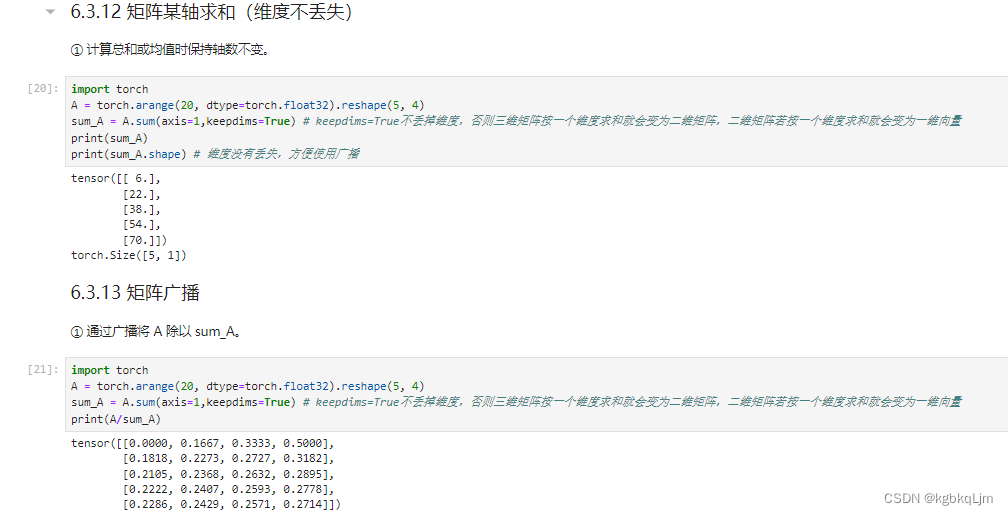
在这里插入图片描述

矩阵按某轴求和（计算后不丢掉维度）、矩阵广播

目的：按照某个维度求和时，不想将该维度丢掉（丢掉后的结果如上面几个图，即如果一个三维矩阵按一个维度求和后会变成二维矩阵，如果一个二维矩阵按一个维度求和会变成一个标量）

实现：设置keepdims=True。好处是可以用于后续实现广播操作
注意：numpy中的广播和pytorch中的广播的要求好像在不同的python版本中有不同？torch中要求广播运算的两个tensor维度必须相同、形状可不同（好像对于新版本的python和pytorch的广播要求和numpy的一致了，具体用到再看）；numpy中在某些维度不同的数组之间也能进行广播

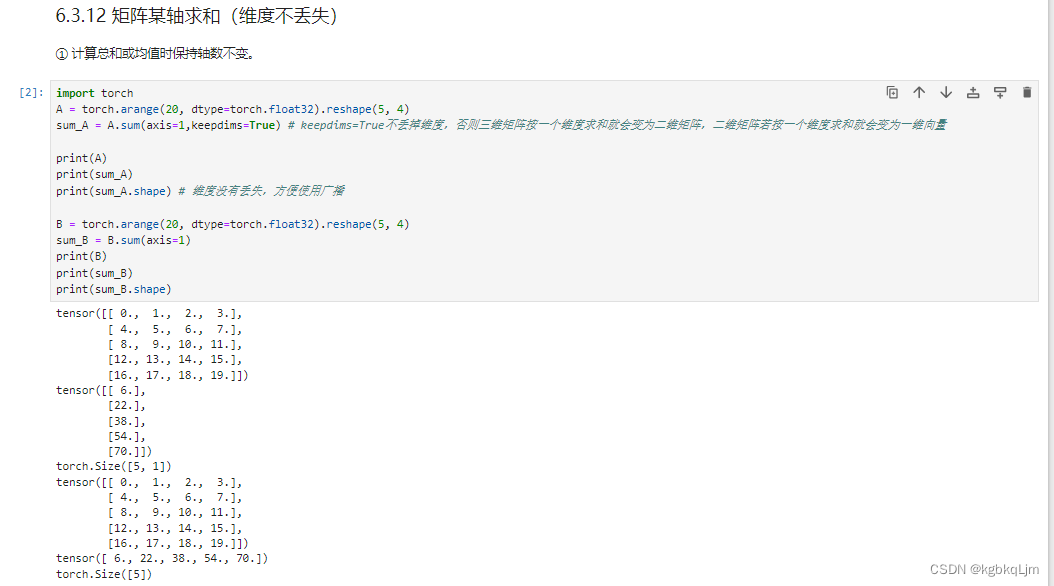
在这里插入图片描述

矩阵某轴累加cumsum（前缀和）、向量点积dot

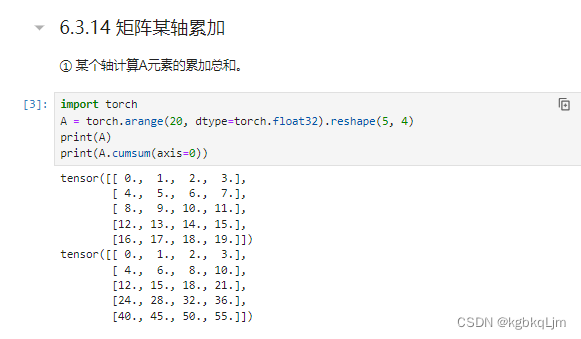
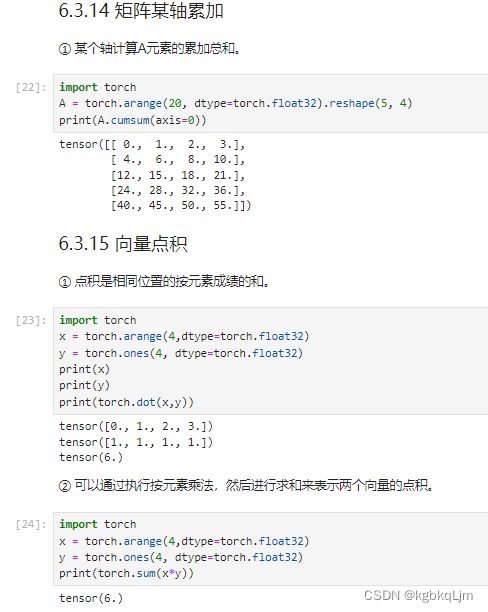
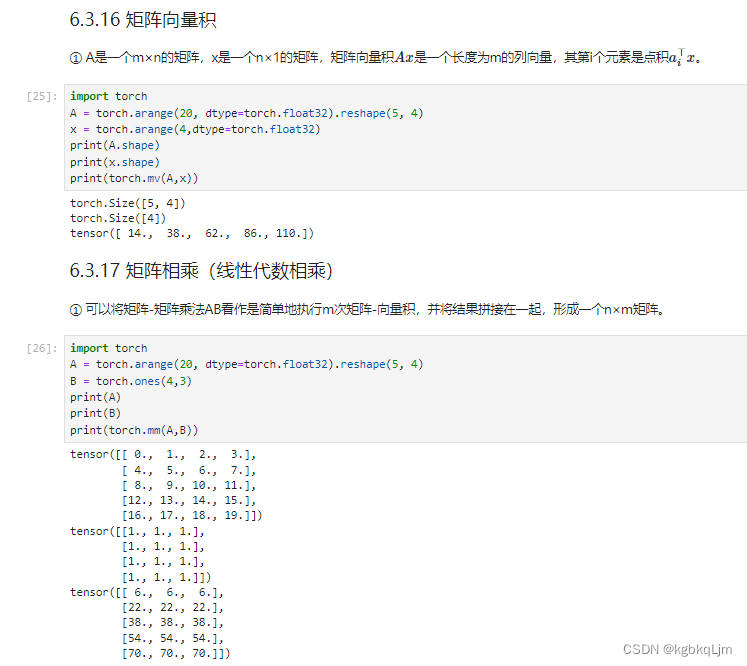
在这里插入图片描述

矩阵向量积(mv ,Matrix Vector Multiplication)、矩阵相乘

注意理解pytorch中轴的方向：torch.Size([4])代表一个长度为4的列向量（可以回看dim=0的方向）
在这里插入图片描述

矩阵L2范数norm、L1范数abs().sum()、F范数norm

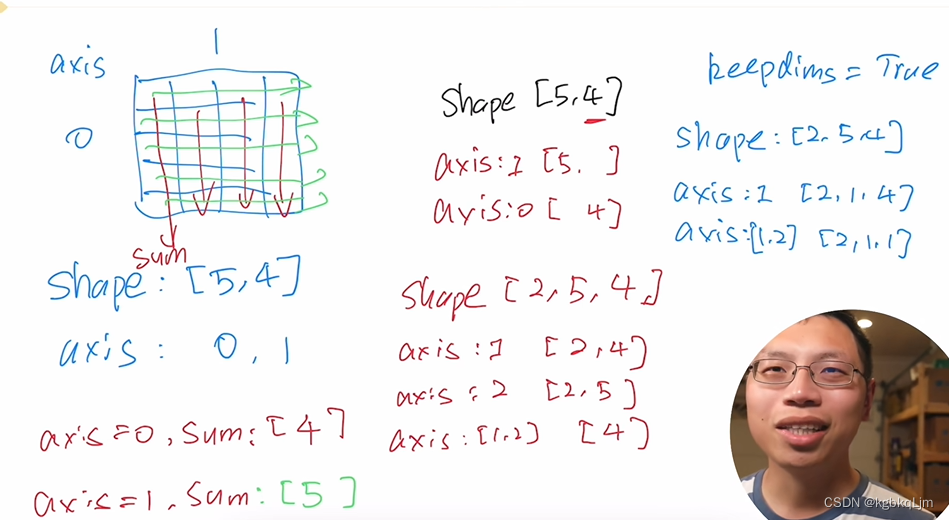
在这里插入图片描述

【补充】按特定轴求和

按那个（或哪些）轴求和，就把 shape的哪个（或哪些）数字消掉并得到最终的shape

如shape[2,5,4]按：
axis=1求和：得到 shape[2,4]
axis=2求和：得到shape[2,5]

如shape[2,5,4]按：
axis=0和2求和：得到shape[5]
axis=1和2求和：得到shape[2]

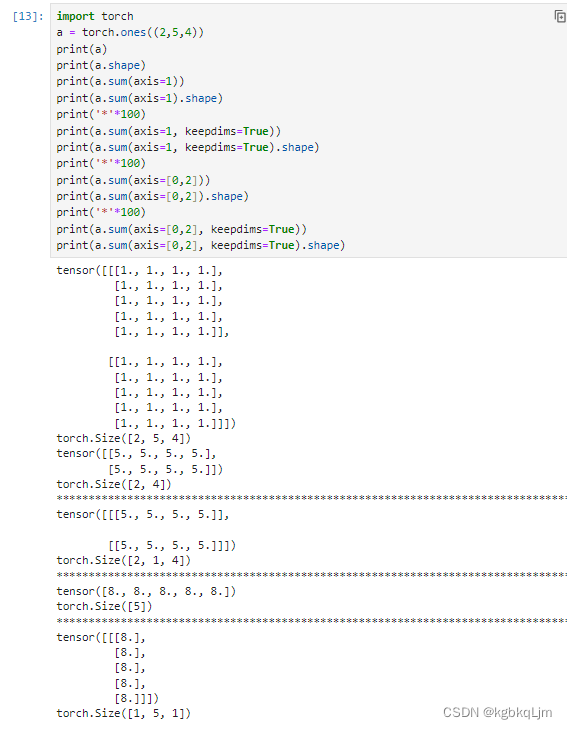
当使用keepdims=true时，按哪个或哪些轴求和，就把对应的shape变为1（右边蓝字）
如shape[2,5,4]按：
axis=1求和：得到shape[2,1,4]
axis=1和2求和：得到shape[2,1,1]
在这里插入图片描述

QA

在这里插入图片描述

1.如果有很多字符串或特征，基于one-hot把其变成0、1，那样就有很多列，变得很稀疏
对机器学习来说，稀疏矩阵不会有很多影响

2.深度学习、机器学习为什么用tensor
统计学更爱用tensor

3.copy和clone
体会深浅拷贝，clone一定是深拷贝，copy可能是浅拷贝

4.可以

5.torch区分行、列向量吗？
（弹幕）因为向量就是一维的，在计算机里就是一个数组，没有行列之分。想要区分，就要按矩阵来看
个人理解：torch中行列向量都是一维向量，一维向量不区分行或列（不像线代那样）。
如果必须要区分，可以用二维数组中存放多个一维数组（每个一维数组中只有一个元素）表示列向量

6.自己看下前面的笔记吧

7.后面讲

8.后面讲（词向量？）

9.机器学习中的张量就是多维数组，和数学中的张量不同

10.【重点体会核心思想和概念，工具只是工具】类似于在不同时代用不同工具，如学车，几十年前用自行车，现在用汽车。
工具只是工具（如python、C++、pytorch）

06-矩阵计算

在深度学习中我们很少对向量的函数求导，绝大多数情况下都是对标量求导，因此之前学的很多向量、矩阵求导是用不到的

标量导数与亚导数

在这里插入图片描述

向量与标量的求导（重点是搞对形状）

要搞清形状：
对于y=f(x)

y标x标时，求导是标（如上节）
y向x标，求导是向量
y标x向时，求导是向量
y向x向，求导是矩阵
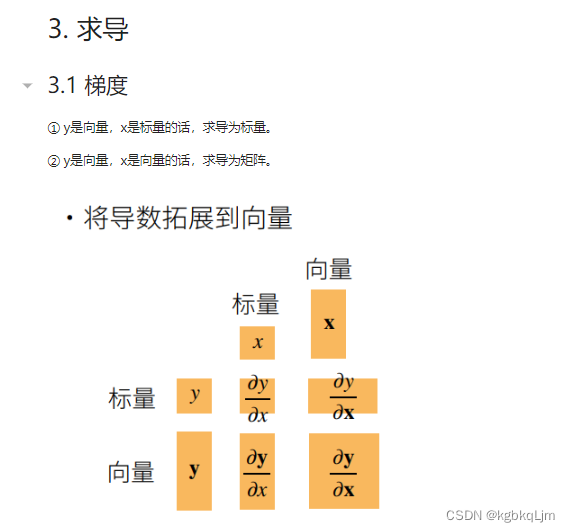
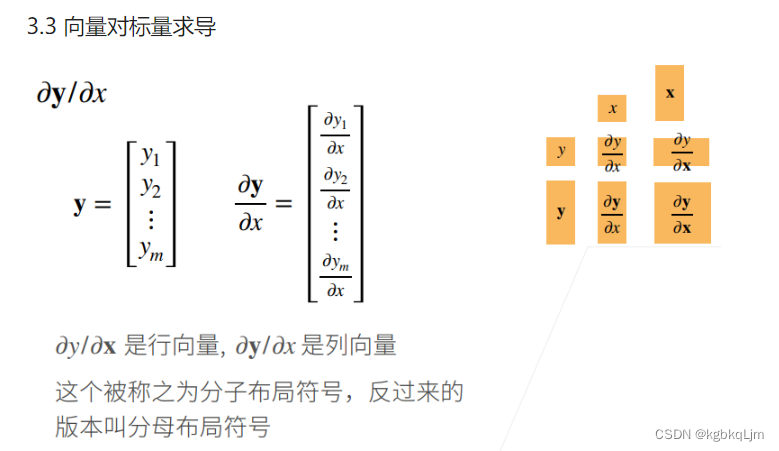
在这里插入图片描述

标量y对向量x求导

弹幕说：别猜了这里的差异是分子布局和分母布局的原因结果遵循分子布局就是行向量遵循分母布局就是列向量

举例：
x是一个长为2的向量，y定义为第一个元素平方+2第二个元素的平方
下图画的椭圆就是 y=x1的平方+2x2的平方
梯度和等高线是正交的（即**【梯度指向的是值变化最大的方向】**）
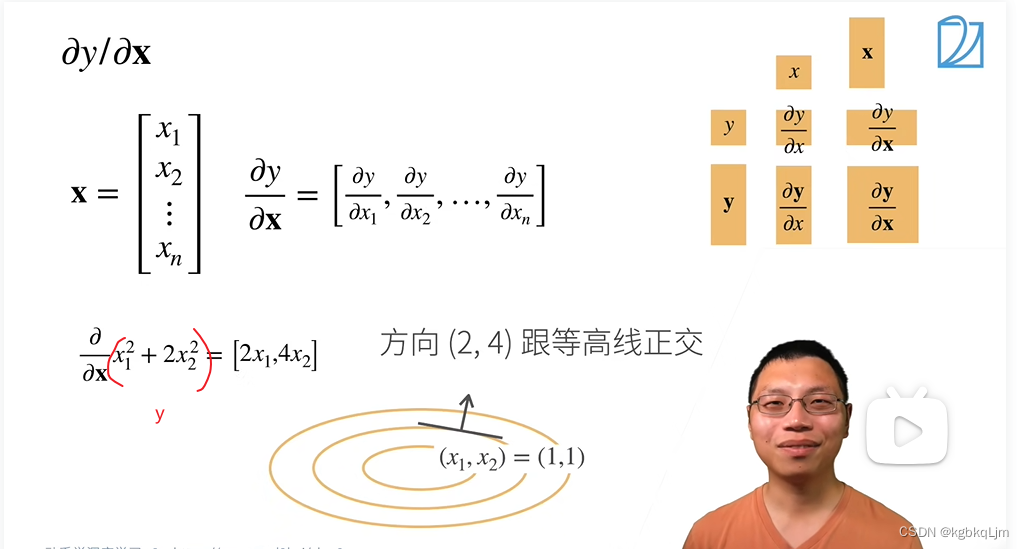
在这里插入图片描述

0T:全0行向量（感觉加粗0相当于列向量，转置变成行向量）
<u,v> ：指向量u和v的内积
弹幕说：L2 norm的平方，平方后根号没了，变成各项x的平方和，然后对x进行求导，每一行就是2xi，然后就是原来列向量x的转置的2倍
在这里插入图片描述

向量对标量求导（分子/分母布局）

列（或行）向量对于标量的导数还是列（或行）向量
在这里插入图片描述

向量y对向量x求导

如x、y都是列向量时
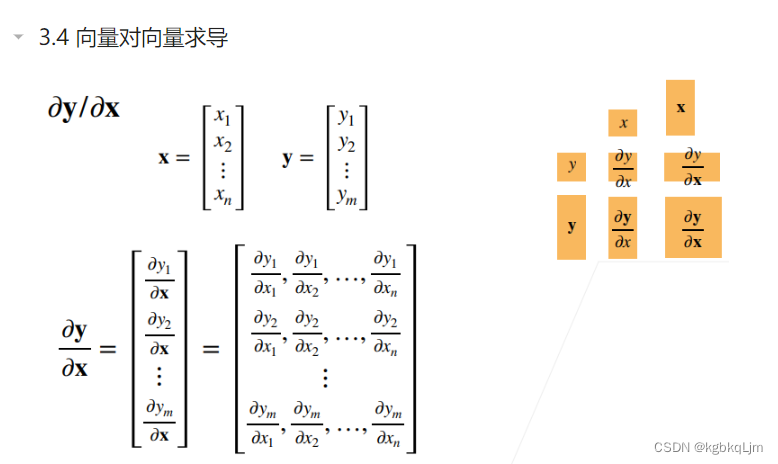
在这里插入图片描述

下图中0是全0矩阵，I是单位矩阵，A是和x无关的矩阵
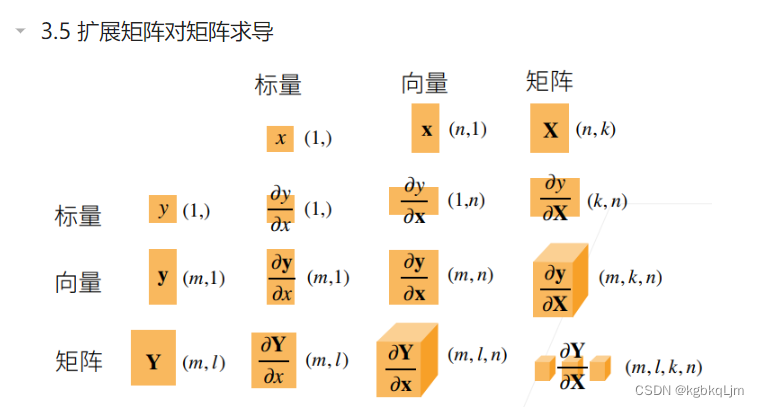
在这里插入图片描述

矩阵对矩阵求导

在这里插入图片描述

QA（接上节）

NP:Non-Polynomial
14.如果是凸函数能拿到最优，如果非凸函数在实际计算中几乎拿不到最优解（纯数学理论或许可能）

07-自动求导

向量链式法则

在这里插入图片描述
<x,w>指向量x和w的内积
因为<x,w>=x^T w

矩阵的例子：
X：mxn的矩阵，w：向量

自动求导

在这里插入图片描述

计算图（原理）

计算图等价于上节我们用链式法则求导的过程，是一个无环图
操作子：一步一步操作
每个圈表示一个输入、一个操作
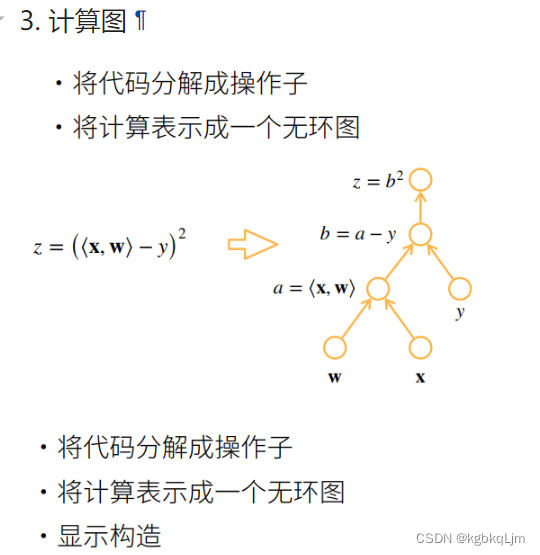
在这里插入图片描述

tf和mxnet都可以显式构造计算图（如下图上面，直接定义出来公式）
在这里插入图片描述

基于计算图的两种自动求导方式

这里是概述原理，应用的时候底层都做好了，不需要自己实现自动求导
【两种方式】正向计算（正向累积）、反向计算（反向累计、即 AI中的反向传播back propagation）（即如下图，括号的计算优先级就展示了计算的方向）
在这里插入图片描述

在这里插入图片描述
正向上节讲了

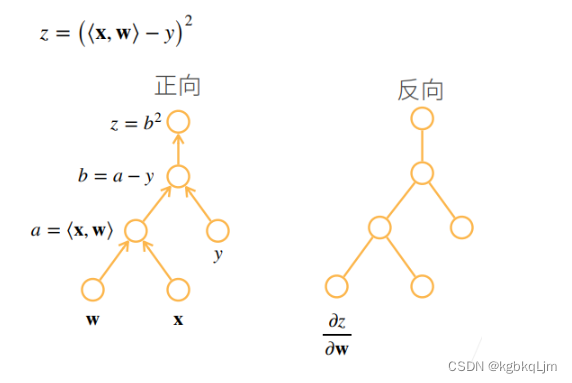
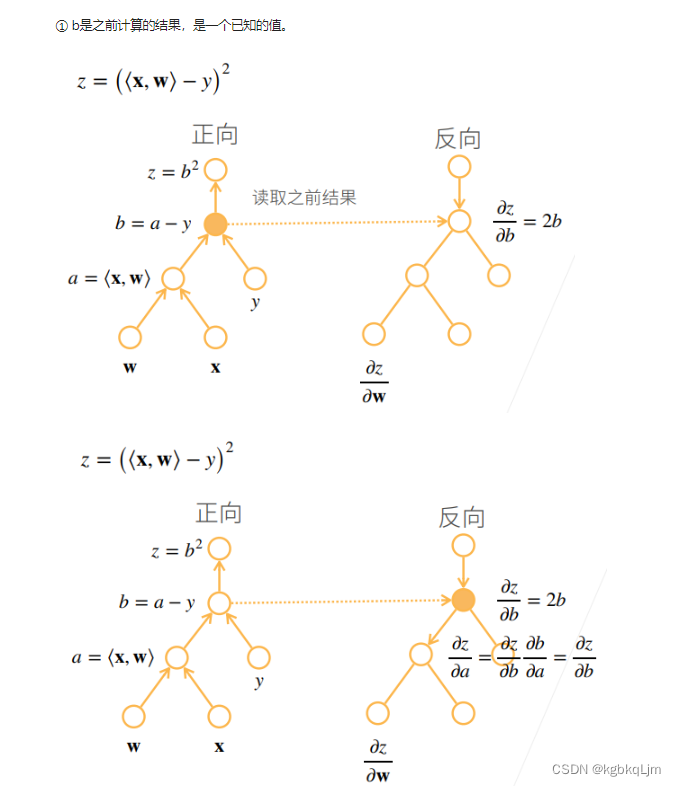
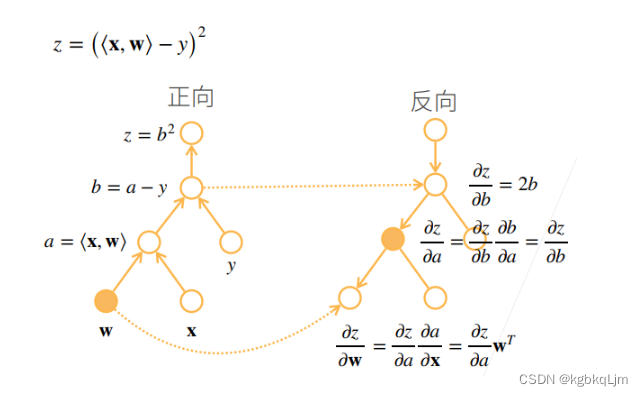
反向累积总结、复杂度

前向计算时，存储所有的中间值，反向时直接用中间结果
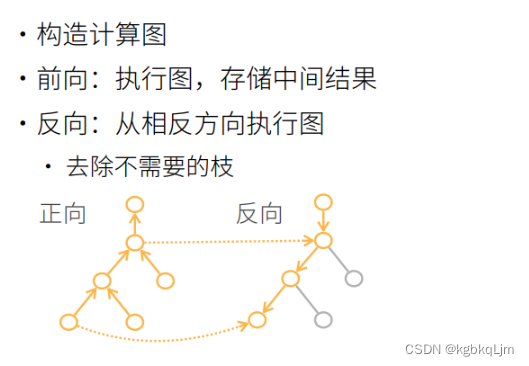
在这里插入图片描述

正向forward和反向backward的计算复杂度差不多。
但反向复杂度的内存复杂度是On（深度神经网络很耗GPU资源）
正向累积内存复杂度O1（因为无论网络多深，都不需要存中间计算结果。但当需要计算一个变量的梯度时需要将整个网络都计算一遍，效率太低）
在这里插入图片描述

【代码】自动求导

【例子1】

x.requires_grad_(True) # 等价于 x = torch.arange(4.0,requires_grad=True)。告诉我们要存储梯度，这样后续就可以直接基于x.grad访问梯度了
在这里插入图片描述
内积：<x,x> 。y对其求导相当于=2*（xT+xT)=4xT

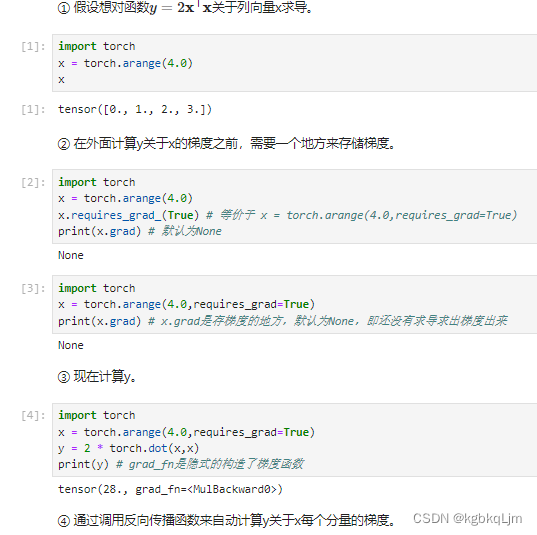
上图中28=2*(0x0+1x1+2x2+3x3)
通过调用反向传播函数来自动计算y关于x每个分量的梯度
利用backward()计算所有梯度，会自动累积到.grad属性中

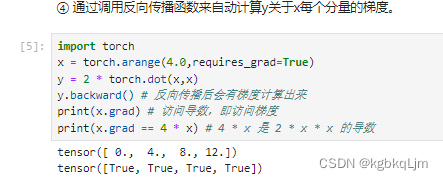
在这里插入图片描述
上图中x = [0. , 1., 2., 3. ]，则对于 y=2*xT和x的内积的 x的梯度（即导数）为 [4x0, 4x1, 4x2, 4x3]

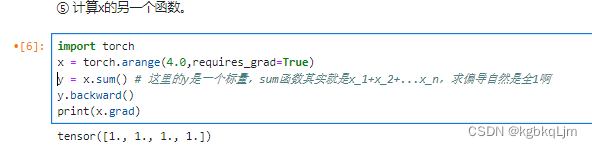
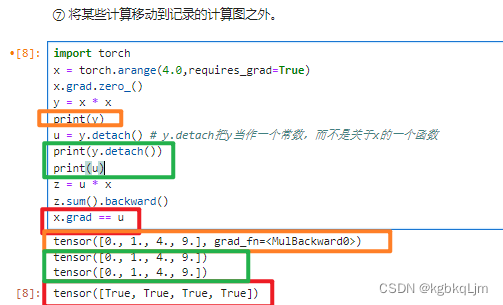
【例子2】下面计算 x的另一个函数（y=x.sum()）：

默认情况下，PyTorch会累积梯度，因此在计算另一个函数时需要清除之前的梯度值

pytorch中_表示重写这个变量，如 x.grad.zero_()重写梯度grad（即把梯度清0）
理论上求向量的sum的梯度：SUM函数其实就是x_1+x_2+…x_n，求偏导自然是全1啊
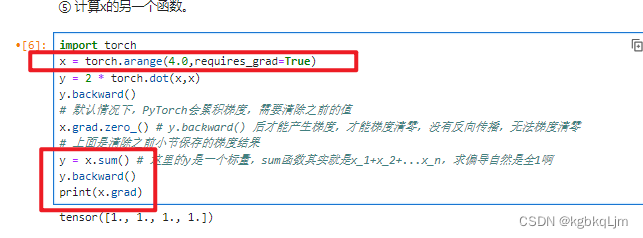
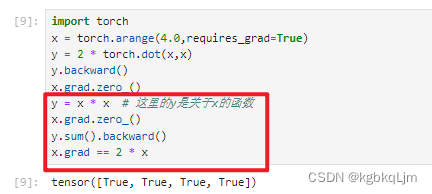
在这里插入图片描述

在这里插入图片描述

【例子3】如 y=x*x假设y和x都是向量时，理论上y是一个矩阵，但是在深度学习中我们很少对向量的函数求导，绝大多数情况下都是对标量求导，因此实际上我们会对y.sum（这就是个标量了）求导而不是直接对y求导(不求和直接算梯度结果是一个矩阵，就越来越复杂了)，因此之前学的很多向量、矩阵求导是用不到的

注：这里的*是哈达玛积（那不就是向量或矩阵按元素计算吗）
x = [0. , 1., 2., 3. ]，则对于 y=x *x的.sum() 为 x1 ^ 2+x2^ 2+x3^ 2…+xn^n，导数即 2x1+2x2+2x3+…+2xn
则 x的梯度（即导数）为 [0.， 2.，4.，6.]

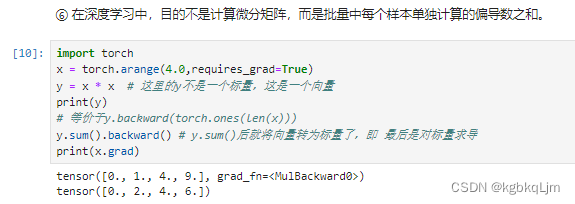
在这里插入图片描述

【例子4】将某些计算移动到记录的计算图之外。

【意义】对于后续网络中，需要固定其中部分参数时，很有用
detach:拆卸脱离
u = y.detach() # y.detach把y当作一个常数，而不是关于x的一个函数，并声明为u，即u是一个常数，值为xx，而不是一个关于x的变量（y此时仍然是 x的函数）
则z就是一个常数u变量x，导数即为常数u
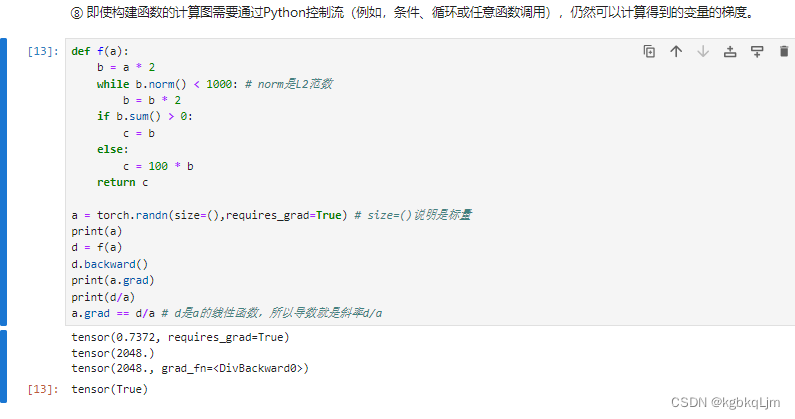
在这里插入图片描述