一. 前言
在游戏程序中,利用空间数据结构加速计算往往是非常重要的优化思想,空间数据结构可以应用于场景管理、渲染、物理、游戏逻辑等方面。
二、多叉树
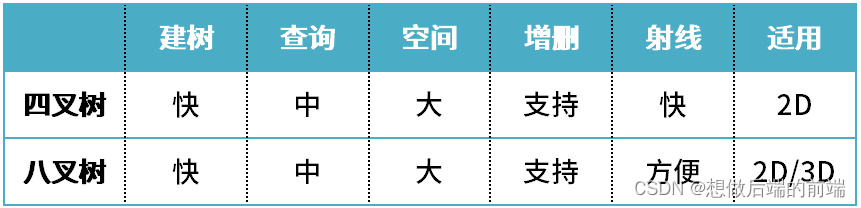
2.1 四叉树
四叉树是很常见的一种 2D 碰撞检测方法,实现手段也五花八门。不过在具体实现中要注意优化细节,控制建树时间消耗与建树空间大小,特别是在 JS 语言环境下。但四叉树的射线检测、区域检测效率比较高,树更新很快,会产生物体多次划分,空间占用大。
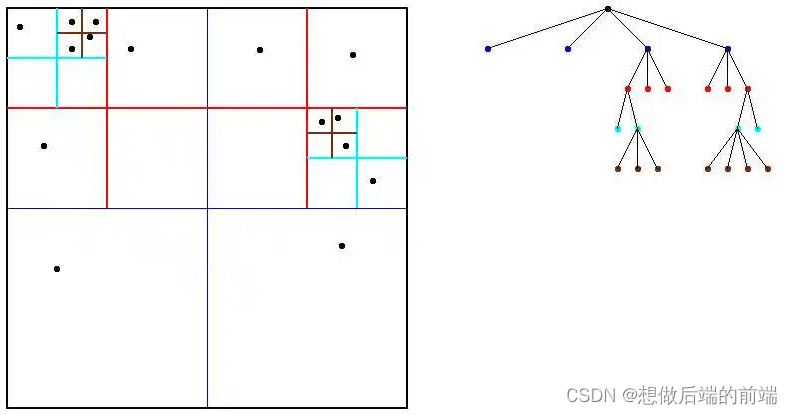
四叉树的结构在空间数据对象分布比较均匀时,具有比较高的空间数据插入和查询效率(复杂度O(logN))。
//示例:一个四叉树节点的简单结构
struct QuadtreeNode {
Data data;
QuadtreeNode* children[2][2];
int divide; //表示这个区域的划分长度
};
//示例:找到x,y位置对应的四叉树节点
QuadTreeNode* findNode(int x,int y,QuadtreeNode * root){
if(!root)return;
QuadtreeNode* node = root;
for(int i = 0; i < N && n; ++i){
//通过diliver来将x,y归纳为0或1的值,从而索引到对应的子节点。
int divide = node->divide;
int divideX = x / divide;
int divideY = y / divide;
QuadtreeNode* temp = node->children[divideX][divideY];
if(!temp){break;}
node = temp;
//如果归纳为1的值,还需要减去该划分长度,以便进一步划分
x -= (divideX == 1 ? divide : 0);
y -= (divideY == 1 ? divide : 0);
}
return node;
}
2.2 八叉树
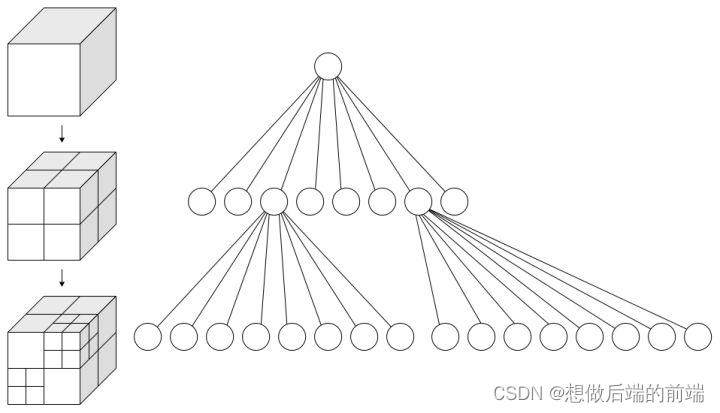
八叉树虽然包围精确性没 BVH 高(可用状态压缩改善)、占用空间较大(过度划分),但是建树和增删非常快,很适合用作物体的筛选。目前 98K 使用了八叉树对模型包围盒进行空间划分,简单高效的建树比精确计算建树(比如 BVH 建树会有大量计算消耗)更加划算。缺点和四叉树一样,射线检测、区域检测较快,树更新很快, 会产生物体多次划分,空间占用大。
2.3 应用
相比网格,四叉树/八叉树主要是多了层次,它们可以进行区域较大的划分,然后可以对各种检测算法进行分区域的剪枝/过滤。
下面提几个应用(实际应用面很广):
- 场景管理
特别适合大规模的广阔室外场景管理。一般来说如果游戏场景是基于地形的(甚至没有高度)(如城市、平原、2D场景),那么适合用四叉树来管理。而如果游戏场景在高度轴上也有大量物体需要管理(如太空、高山),那么适合用八叉树来管理。 - 碰撞检测
类似上面感知检测。不同划分区域保证不会碰撞的情况下,就能快速过滤与本物体不同区域的其他潜在物体碰撞。 - 光线追踪(Ray Tracing)过滤
光线追踪渲染,可使用八叉树来划分3D空间区域,从而过滤掉大量不必要的区域。
三、二叉树
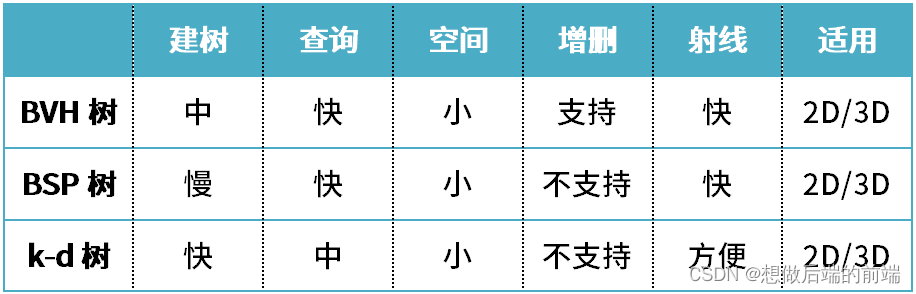
3.1 BVH树
四叉树和八叉树是以平均空间来划分物体,划分算法简单,而 BVH 是对当前物体集合进行空间的划分,追求左右空间大小相对均衡且无相交。BVH 构建的一般是二叉树,划分算法复杂。
主流物理引擎都有采用 BVH(层次包围盒树 (Bounding Volume Hierarchy Based On Tree)),因为其功能支持完备、查找精确性高、性能不俗。但是其在建树和增删改时要维护平衡树,消耗很大。针对这个问题,有一些时序性的空间优化方法,通过减少增删改达到优化目的,感兴趣的朋友可以参考各大物理引擎中的实现方法。
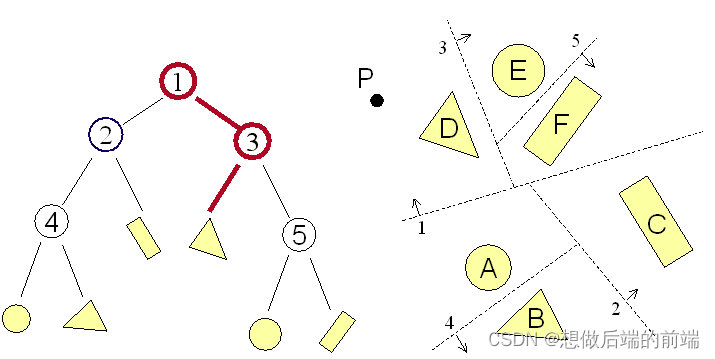
3.2 BSP树
BSP(Binary Space Partitioning Tree),二维空间分割树,非常经典,1993年在知名游戏 DOOM 里第一次被应用,早期 CS 也是用 BSP 来做地形碰撞。BSP 通常通过计算得到一个合理的任意角度片面或者法线,然后对空间进行划分。标准的 BSP 虽然高效,但树构建非常消耗时间,通常都是编辑器预处理,比较适合静态模型或者静态场景使用。
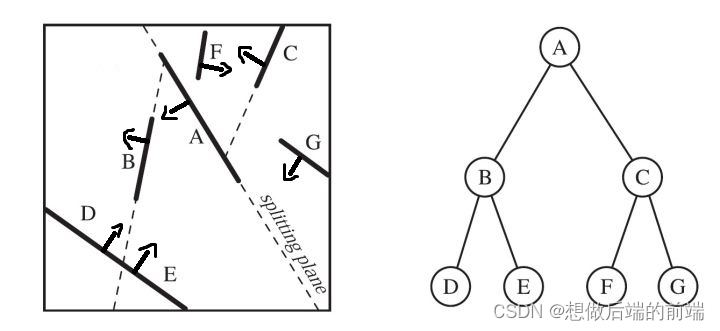
3D空间下要构造一棵较平衡的BSP树,则需要尽可能每次划分出一个节点时,让其左子树节点数和右子树节点数相差不多:
- 在一个平面形状集合里,用其中一个平面构造一个BSP树节点时,需满足它前方的平面形状数和后方的平面形状数之差 小于
一定阈值;若超过阈值则尝试用下一个形状来构造。 - 一个麻烦的问题是当2个平面形状是相交时,即出现平面形状既可以在前方也可以在后方的情况。这时候就需要一个将该形状切割成两个子形状,从而可以一个添加在前方,一个添加在后方,避免冲突。
- 构造完一个节点则移除对应的平面,该节点前面的平面形状和后面的平面形状则作为两个子平面形状集合。
- 对这两个子集合以重复步骤1、2继续构造出两个子节点,并作为本节点的左右儿子。
- 最后所有平面形状都被用于构造节点,组成了一棵BSP树。
//BSP tree节点结构示例
class BSPTreeNode {
Plane plane; //平面
BSPTreeNode* front; //前向的节点
BSPTreeNode* back; //后向的节点
//Data data; //数据
};
由于需要进行N次划分,每次划分后,要在子集合里一个个挑选合适的平面(需要logN次遍历),为了评定合适又需要与子集合里所有其它形状比较前后位置(需要logN次比较),因此可以知道BSP树构造的平均时间复杂度为 O(Nlog²N)
判断点在平面前后的算法:平面的法向量(A,B,C),则平面的方程为:Ax + By + Cz + D = 0;
将点(x0,y0,z0)代入方程得到 distance = Ax0 + By0 + Cz0 + D;
若 distance < 0 则在平面背后
若 distance = 0 则在平面中
若 distance > 0 则在平面前方
3.3 k-d树
k-d树((k-dimensional tree))是一棵二叉树,其每个节点都代表一个 k维坐标点:
树的每层都是对应一个划分维度(取决于你定义第i层是哪个维度)
树的每个节点代表一个超平面,该超平面垂直于当前划分维度的坐标轴,并在该维度上将空间划分为两部分,一部分在其左子树,另一部分在其右子树
实际上,k-d树就是一种特殊形式的BSP树(轴对齐的BSP树)。
//一种实现方式示例:二维k-d树节点
class KdTreeNode{
Vector2 position; //位置
int dimension; //当前所属层的维度
KdTreeNode* children[2]; //两个子树
//Data data; //数据
};
k-d 树是一种特殊的 BSP 树,它基于动态计算的三个轴进行划分。k-d 树相比 BSP 可能精确性没那么高,但是建树时间大大减少,因为对轴划分算法简单,所以很适合使用
举例,一棵k-d树(k=2)的结构如图:
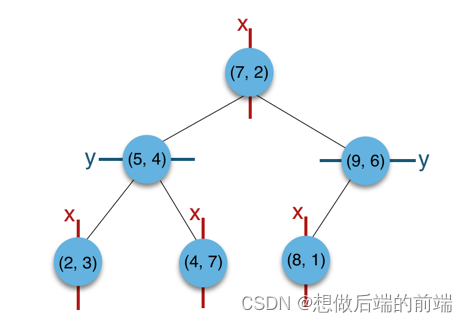
根据第一层划分维度为X,第二层为Y,第三层为X,
所以该k-d树(k=2)对应代表划分的空间,看起来应该是这样的:
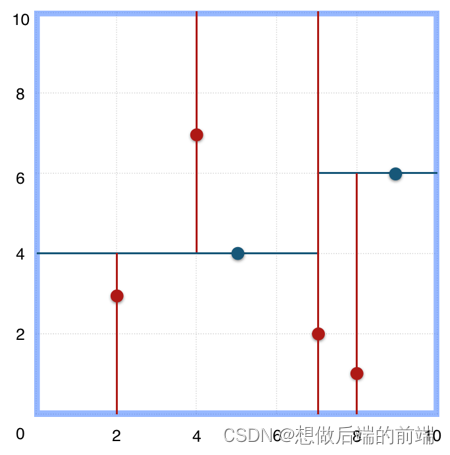


![[AutoSar]BSW_OS 02 Autosar OS_STACK](https://img-blog.csdnimg.cn/direct/893a7f4747e245a699486ee57a139a65.png)