集合的定义
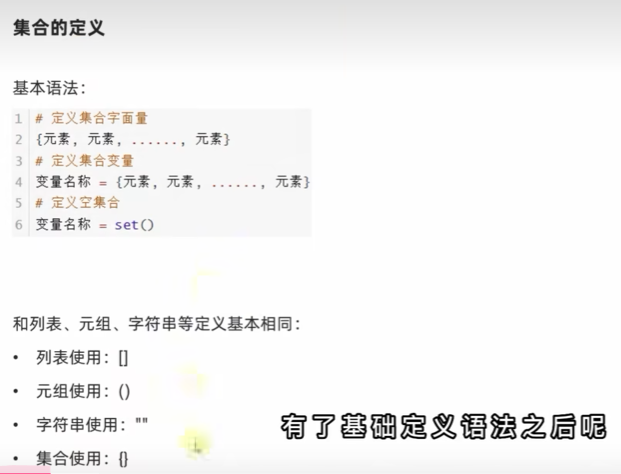
"""
演示数据容器集合的使用
"""
#定义集合
my_set={"计算机","0854","考研上岸","计算机","0854","考研上岸","计算机","0854","考研上岸"}
my_set_empty=set()
print(f"my_set的内容是:{my_set},类型是{type(my_set)}")
print(f"my_set_empty的内容是:{my_set_empty},类型是{type(my_set_empty)}")
可以发现已经将重复的元素进行去掉,且顺序也发生的错乱
集合常用修改操作

添加新元素set.add()
#添加新元素
my_set={"计算机","0854","考研上岸","计算机","0854","考研上岸","计算机","0854","考研上岸"}
my_set.add("Python")
my_set.add("0854")
print(f"my_set添加元素后的结果:{my_set}")
新添加的元素python已经成功添加,但是添加的元素0854在以前的列表中已经包含了,所以结果中不在显示,只显示一个0854
移除元素set.remove()
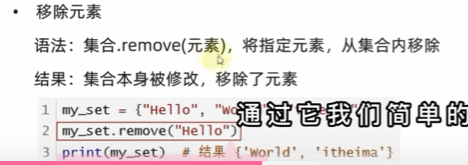
#移除元素
my_set={"计算机","0854","考研上岸","计算机","0854","考研上岸","计算机","0854","考研上岸"}
my_set.remove("计算机")
print(f"my_set移除计算机后的结果是{my_set}")
随机取出一个元素set.pop()

#随机取出一个元素
my_set={"计算机","0854","考研上岸","计算机","0854","考研上岸","计算机","0854","考研上岸"}
element=my_set.pop()
print(f"集合被取出元素是:{element}")
清空集合set.clear()
#清空集合
my_set={"计算机","0854","考研上岸","计算机","0854","考研上岸","计算机","0854","考研上岸"}
my_set.clear()
print(f"集合被清空啦,结果是:{my_set}")
取出两个集合的差集:集合1.difference(集合2)

#取2个集合的差集
set1={1,2,3}
set2={1,5,6}
set3=set1.difference(set2)
print(f"取出差集后的结果是:{set3}")
print(f"取出差集后set1的结果是:{set1}")
print(f"取出差集后set2的结果是:{set2}")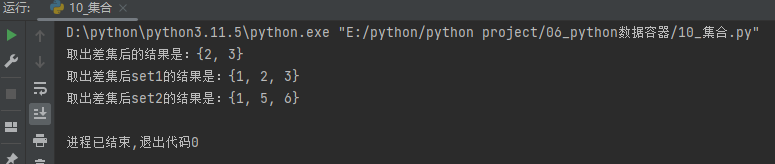
消除两个集合的差集:集合1.difference_update(集合2)

#消除2个集合的差集
set1={1,2,3}
set2={1,5,6}
set1.difference_update(set2)
print(f"消除差集后,集合1结果:{set1}")
print(f"消除差集后,集合2结果:{set2}")
两个集合的合并:集合1.union(集合2)

#2个集合合并为1个
set1={1,2,3}
set2={1,5,6}
set3=set1.union(set2)
print(f"两个集合合并结果:{set3}")
print(f"合并后集合1:{set1}")
print(f"合并后集合2:{set2}")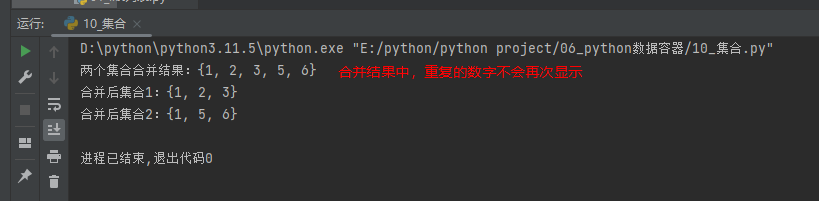
统计集合元素的数量len()
#统计集合元素数量len()
set1={1,2,3,4,5}
num=len(set1)
print(f"集合内的元素数量有:{num}")
注意:这里是数字5是说不重复的数字一共有5个,若有重复的数字将不计入在内
集合的for循环遍历,不支持下标索引,故不支持while循环遍历
#集合的遍历,集合不支持下标索引,所以不能使用whlie循环遍历,可以用for循环
set1={1,2,3,4,5}
for element in set1:
print(f"集合元素有:{element}")




课后练习–信息去重
有如下列表:
my_list=['计算机','程序员','计算机','程序员‘,'jisuanji','chenxuyuan','jisuanji','chenxuyuan']
1.请定义一个空集合
2.通过for循环遍历列表
3.在for循环中将列表的元素添加至集合
4.最终得到元素去重后的集合对象,并打印输出
"""
演示集合的课后练习题
my_list=['计算机','程序员','计算机','程序员‘,
'jisuanji','chenxuyuan','jisuanji','chenxuyuan']
"""
my_list=['计算机','程序员','计算机','程序员',
'jisuanji','chenxuyuan','jisuanji','chenxuyuan']
#定义一个空集合
my_set=set()
#通过for循环遍历列表
for element in my_list:
#在for循环重将列表的元素添加至集合
my_set.add(element)
#最终得到元素去重后的集合对象,并打印输出
print(f"列表的内容是:{my_list}")
print(f"通过for循环后,得到的集合对象是:{my_set}")