普通线段树

线段树是什么

我们要学习线段树，首先要了解线段树的结构长什么样。

线段树是一颗二叉树，树上的节点储存数据（可以是值、字符串、数组、多个值）。

作用

一般来说，线段树是用来维护一个数组的。

数据储存

线段树每个节点上储存数组上区间 $[l,r]$ 的相应数据，根节点储存整个数组的数据。

每个节点的左右儿子分别储存区间 $[l,\lfloor \frac{l+r}{2}\rfloor ]$ 和 $[\lfloor \frac{l+r}{2}\rfloor +1,r]$ 的数据。

一直分割到叶子节点，所以每个叶子节点上 $l=r$，只储存数组上一个位置的数据。

一般情况下，节点 $o$ 的值储存在下标 $o$ 的位置，节点 $o$ 的左儿子为节点 $o\times 2$，右儿子为 $o\times 2+1$。

但有时则自由定义节点 $o$ 的左右儿子，并另行记录。

具体操作

单点修改区间查询

有一个长度为 $n$ 的数组 $a$，有 $m$ 个操作

1. 询问 $a$ 在 $[s,t]$ 的和
2. 将 $a_x$ 的值加 $v$

$1\le n,m\le 10^6$

单点修改

修改单个点，代表着我们需要修改线段树上所有包括这个点的区间。

很显然，如果一个更大的区间 $[l,r]$ 不包括 $x$，那么这个区间的所有子区间都不包括 $x$。

所以我们从根节点开始修改。

每次在左右儿子中找出包括 $x$ 的节点来修改。

然后继续往下递归，直到没有左右儿子。

时间复杂度 $O(\log n)$

如果不用线段树维护，单点修改完全可以非常简单做到 $O(1)$。是不是觉得线段树是垃圾呢

区间查询

线段树显然不是垃圾，不然发明他干啥。闲着没事干？

线段树的作用就体现在这了。

如果不用线段树，区间查询我们需要挨个将每个点的值访问一遍才能求和。

但线段树已经将部分区间的和帮我们求好了。

我们只需要把询问区间 $[s,t]$ 分解成线段树求过的若干区间，再求和即可。

对于当前遍历到的节点 $u$，我们要返回 $[l_u,r_u]$ 内 $[s,t]$ 的和。

如果 $[l_u,r_u]$ 被完全包括在 $[s,t]$ 中，$[l_u,r_u]$ 内 $[s,t]$ 的和就是 $[l_u,r_u]$ 的和，直接 return 即可。

如果 $u$ 儿子的区间（即 $[l_v,r_v]$）与 $[s,t]$ 有交集，则遍历 $u$ 所有有交集的儿子，返回儿子答案的和。

时间复杂度 $O(\log n)$

比不用线段树快了吧。

区间修改单点查询

有一个长度为 $n$ 的数组 $a$，有 $m$ 个操作

1. 询问 $a_x$ 的值
2. 将 $a$ 在区间 $[s,t]$ 内的所有值加 $v$

$1\le n,m\le 10^6$

区间修改

区间修改显然无法将与修改区间有交集的区间值全部更改，怎么办？

需要用到差分思想。

如果我们在单点查询的时候不查询单个点，而是改成前缀和，查询 $[1,x]$ 的和来作为答案。

我们区间修改就可以只修改两个点 $s$ 和 $t+1$ 了。

我们把 $b_s$ 加 $v$，$b_{t+1}$ 减 $v$。

因为如果查询前修改了 $[s,t]$ 的值，查询时 $x$ 在 $[s,t]$ 内，则 $[1,x]$ 会包括 $s$ 但不包括 $t+1$，值就比修改前的正好增加了 $v$。

如果查询时 $x$ 在 $[t+1,n]$ 内，则 $[1,x]$ 会包括 $s$ 和 $t+1$，相互抵消，值依旧不变。

单点查询

通过刚才分析，单点查询改成查询 $[1,n]$ 即可。

区间修改区间查询

有一个长度为 $n$ 的数组 $a$，有 $m$ 个操作

1. 询问 $a$ 在 $[s,t]$ 的和
2. 将 $a$ 在区间 $[s,t]$ 内的所有值加 $w$

$1\le n,m\le 10^6$

这下好了，不能使用差分思想了。因为询问也变成区间的了。

怎么办？

区间修改

我们需要一个方法，使得能在 $O(\log n)$ 的时间内完成区间修改操作。

我们尝试使用类似于区间查询时的做法。

对于当前遍历到的节点 $u$，我们要修改 $u$ 储存的值使得其符合修改 $[s,t]$ 后 $u$ 所代表的区间 $[l_u,r_u]$ 内值的和。

如果 $[l_u,r_u]$ 被完全包括在 $[s,t]$ 中，则表示 $[l_u,r_u]$ 内所有值都需要增加 $w$。

我们又知道区间 $[l_u,r_u]$ 的长度，所以我们能够直接算出节点 $u$ 修改后要增加的值，即 $(r_u-l_u+1)\times v$。

那 $u$ 子树怎么办？我们现在没时间处理，于是打上一个 $lazytage$ 懒标记，lazy[u] += v，让之后再来处理。

什么时候处理？遇到就处理。

当区间 $[l_u,r_u]$ 没有被完全包括在 $[s,t]$ 中时 ，就意味着我们要访问儿子节点。

这时候，就顺带处理 $laz{y}_u$，也就是懒标记下传，我们将两个儿子的 $lazy$ 都加上 $laz{y}_u$，两个儿子的值都增加其所代表区间长度乘上 $laz{y}_u$。最后，不要忘了懒标记清零，lazy[u] = 0。

懒标记下传后，我们遍历代表区间与 $[s,t]$ 有交集的儿子。

然后用儿子的信息更改 $u$ 的信息。

时间复杂度 $O(\log n)$

区间查询

同理，区间查询与原来单点修改时一样。

只不过增加了懒标记下传过程而已。

线段树优化

标记永久化

线段树使用中的一个技巧，即不下传懒标记。

如何实现？我们在区间查询的时候，路过标记时将标记的影响添加到答案上。

线段树扩展

动态开点线段树

如果线段树空间复杂度太高，且初始每个节点数据基本统一，则可以使用动态开点线段树。

动态开点线段树就不能使用 $o\ast 2$ 的方法来表示儿子节点了。

需要另开数组或者用结构体储存左右儿子的下标。

当要访问一个节点 $u$ 的左或右儿子时，若 $u$ 要访问的儿子还未创建，则根据初始节点数据来创建一个节点 $v$。并将 $u$ 的儿子标记为 $v$。

即需要节点时才创建节点。

可持久化线段树

一个记录历史版本的线段树。

具体是什么样呢？非常简单。

直接记录历史版本非常容易爆空间，所以我们只需要想一个办法来减少空间使用即可。

我们发现因为每次只修改部分值，所以历史版本有很多重复节点。

我们只需要不新开重复节点就行了。每次只增加修改了的节点。

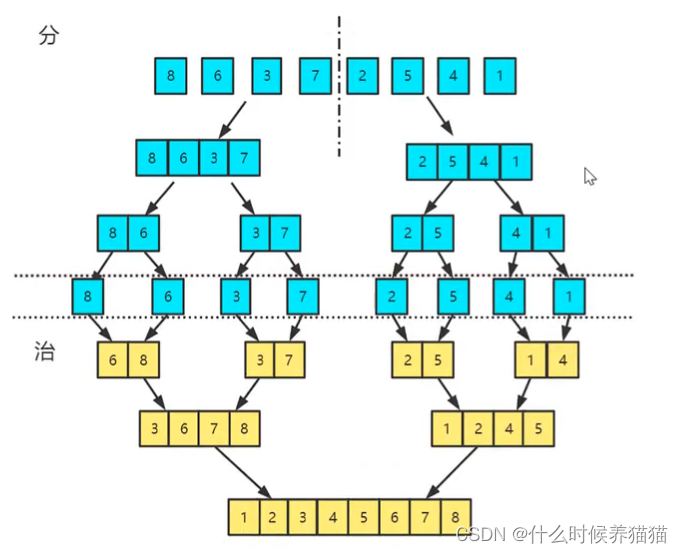
具体来说是这样的（借了一下这篇文章里的图，我不想自己画了 ）：

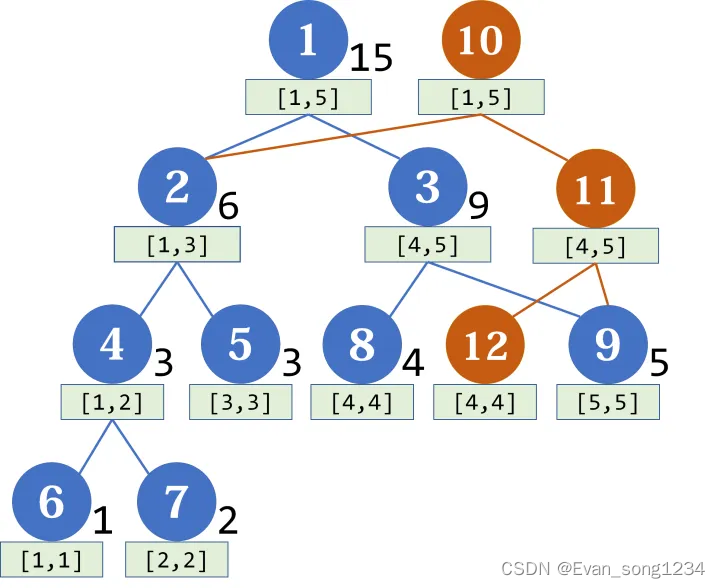
相信大家一看就懂。

李超线段树

李超线段树一般用于解决坐标系中线段相关问题，有时可以转化成其他形态。

有一个平面直角坐标系，$m$ 个操作。

1. 添加一个左右端点为 $(x_1,y_1),(x_2,y_2)$ 的线段。（$x_1\ne y_1$）
2. 询问与直线 $x=k$ 相交线段的交点中纵坐标最大的交点的纵坐标。

$1\le n,m\le 10^6$

我们可以把第一个操作看成区间修改，第二个操作看成单点查询

于是问题就好办了。

接下来讲一下两个操作的步骤：

区间修改

对于每个线段我们可以看成一个定义域为一段区间的一次函数。

现在要新增一个定义域为一段区间的一次函数 $f$。

考虑这样的方法：我们每个节点不储存信息，只打懒标记（懒标记为一个函数），并使用标记永久化技巧。

询问时，则取节点区间包含了 $x=k$ 的节点的懒标记中在 $x=n$ 上取值最大懒标记。

假设我们现在递归到了节点 $u$，其懒标记为 $g$、对应区间为 $[l,r]$，而且 $[l,r]$ 被 $f$ 定义域覆盖。

如果在 $x=\lfloor \frac{l+r}{2}\rfloor$ 处 $f$ 比 $g$ 取值大，则将 $f$ 与 $g$ 交换。

接下来只讨论另一种情况。

节点 $u$ 的懒标记已经不需要更新了，但我们还需要判断其左右儿子懒标记是否需要更新，因为可能在左右儿子的区间中点处 $f$ 取值比 $g$ 取值大。

所以我们可以分类讨论 $f$ 和 $g$ 斜率正负号、或者直接解出 $f$ 与 $g$ 的交点（也可以用其他方法）来判断左右儿子懒标记是否需要更新。

查询交点

查询的时候，我们在所有 节点区间 包含 $k$ 的节点的懒标记中寻找出在 $x=k$ 取值。