目录
希尔排序
1.算法描述
2.算法的实现
归并排序
4.1算法描述
2.算法实现
希尔排序
1.算法描述
1959年shell发明,第一批突破O(n2)时间复杂度的排序算法,是简单插入排序的改进版。它与插入之处在于,它会优先于举例比较远的元素。希尔排序又叫 缩小增量排序
算法的核心思想是将整个待排序的记录序列分割为若干个子序列分别进行直接插入排序,具体算法描述:
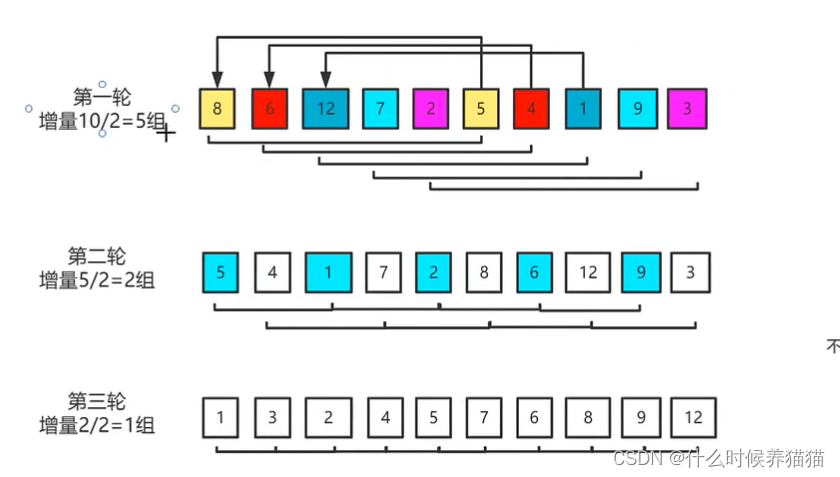
1.先根据数组的长度/n,获得增量K(第一次n为2)
2.按增量序列个数k进行分组,一般可以分为k组;
3.根据已分好的组进行插入排序;(每组排序,根据对应的增量来找当前组的元素)
4.当每组排序完毕之后,回到第一步将n*2再次分组进行插入排序,直到最终k=1的时候,在执行一次插入排序完成最终的插入排序。
2.算法的实现
分解1:先将数组根据长度分为length/2(增量),并将第一组的元素进行插入排序
分解2:排序完毕之后,将n*2再次分组进行插入排序
分解3:执行完第一轮之后,再继续分组执行分解1和分解2的操作,最终到无法分组,排序完成
法1:
package Sort;
public class ShellSort {
public static void main(String[] args) {
int[] arrs={8,6,12,7,2,5,4,1,9,3};
//分组
int group=arrs.length/2;
while (group!=1){
//分组
group=group/2;
// System.out.println("输出第一组的元素");
for (int i = 0; i < group; i++) {
int j=i;
while(j+group<arrs.length){
int insert=j+group;
while ((insert-group) >= 0){
if(arrs[insert-group]>arrs[insert]){
//进行交换
int temp=arrs[insert-group];
arrs[insert-group]=arrs[insert];
arrs[insert]=temp;
//插入的指针要向前移动
insert=insert-group;
}else{
break;
}
}
//j进行增量
j=j+group;
}
}
}
for(int i=0;i<arrs.length;i++){
System.out.println(arrs[i]);
}
}
}法二:
package Sort;
public class text {
public static void main(String[] args) {
int[] arrs ={8,6,1,7,2,5,4,12,9};
//希尔排序
for(int gap=arrs.length/2; gap >0; gap/=2){
//插入排序
for(int i=gap;i<arrs.length;i++){
int insert = arrs[i];
int p=i;
while (p-gap >= 0 && arrs[p-gap] > insert){
arrs[p]=arrs[p-gap];
p-=gap;
}
arrs[p]=insert;
}
}
//输出结果
for(int i = 0; i < arrs.length;i++){
System.out.println(arrs[i]+",");
}
}
}归并排序
4.1算法描述
归并排序是利用归并的思想实现的排序方法,该算法采用经典的分治策略即将问题分成一些小的问题然后递归求解,而治的阶段将得分的阶段得到的答案“修补”在一起,及分而治之。
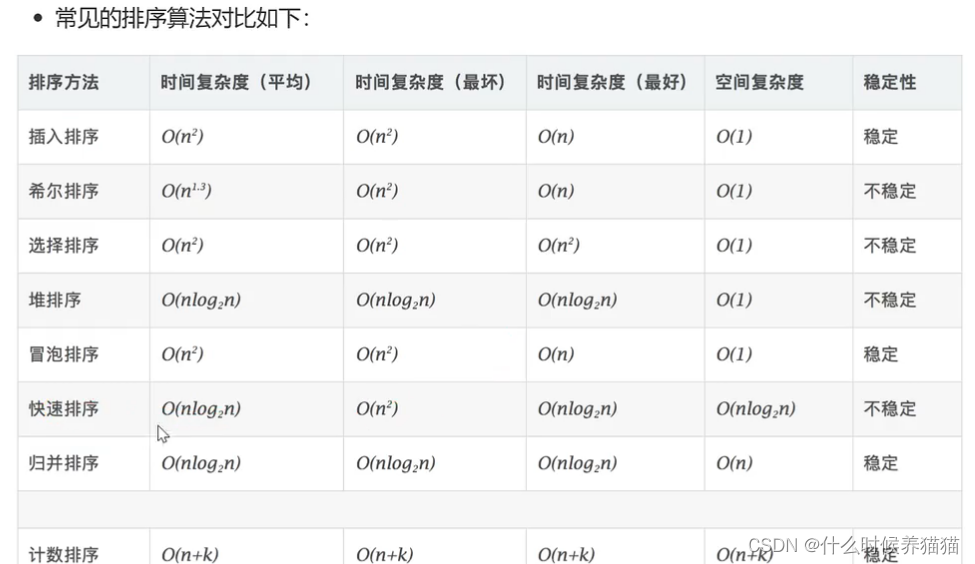
归并排序是稳定排序,它也是一种十分高效的排序,能利用二叉树特性的排序一般性能都不会太差。java中Array.sort()采用了一种名为TimSort的排序算法,就是归并排序的优化版本。从上文的图中可以看出,每次合并操作平均时间复杂度为O(n),而完全二叉树的深度为|nlogn|。并且,归并排序的最好,最坏,平均时间复杂度均为O(nlogn)。
归并排序的核心思想是先分再治,具体算法描述如下:
1.先将未排序数组/2进行分组,然后再将分好组的数组继续/2再次分组,直到无法分组,这个就是分的过程。
2.然后再把两个数组大小为1的合并成大小为2的,再把两个大小为2的合并成4的,同时在合并过程中完成数组的排序,最终直到全部小的数组合并起来,这个就是治的过程。
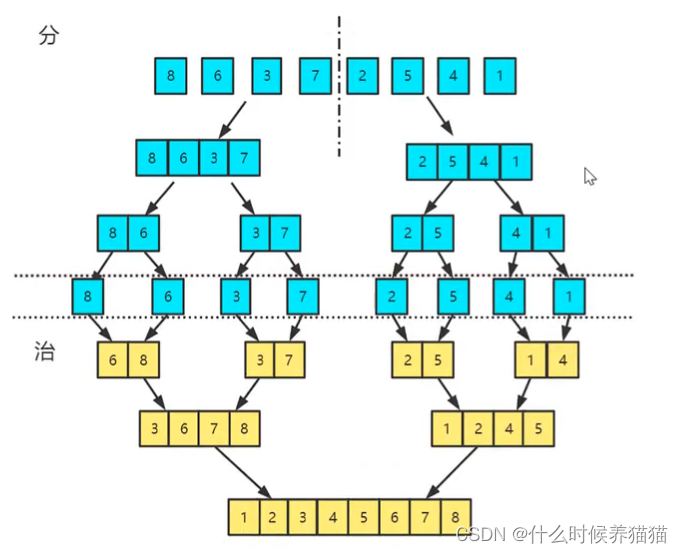
治的过程中会分为两个驻足两个游标,和一个新的数组。
1.分别比较两个游标对应的数组的元素,将小的插入到新的数组中
2.然后向后移动较小的数组的游标,继续进行比较
3.反复前面两步,最终将两个数组的元素合并到新的数组中
2.算法实现
分解1:先实现分的思想,讲数组分解进行实现
1.先获取数组的中轴,然后以中轴讲数组分为两个部分
2.使用递归分别执行两部分分解
分解2:实现具体治的过程,讲左右两个数组合并到一个临时数组中
1.分别设计两指针i和j,遍历左右两个数组,取出元素进行比较,将小的元素放到临时数组中
2.然后将左右剩下的元素放到数组中
3.将排序好的数组中的元素返回到未排序的数组中
package Sort;
public class MergeSort {
public static void main(String[] args) {
int[] arrs = {8, 6, 1, 7, 2, 5, 4, 12, 9};
//归并函数
mergesort(arrs, 0, arrs.length - 1);
for (int i = 0; i < arrs.length; i++) {
System.out.println(arrs[i]);
}
}
//实现归并排序
public static void mergesort(int arrs[], int start, int end) {
if (start < end) {
int mid = (start + end) / 2;
mergesort(arrs, start, mid);
mergesort(arrs, mid + 1, end);
//治的过程,实现插入并完成
int[] temp = new int[end + 1];
int left = start;//左边数组的指针
int right = mid + 1;//右边数组的指针
int p = 0;//临时数组的指针
//遍历左右两个数组,将较小的元素插入到临时数组中
while (left <= mid && right <= end) {
if (arrs[left] <= arrs[right]) {
temp[p++] = arrs[left++];
} else {
temp[p++] = arrs[right++];
}
}
//再将左右剩余的元素插入的临时数组中
while (left <= mid) {
temp[p++] = arrs[left++];
}
while (right <= end) {
temp[p++] = arrs[right++];
}
//将p重置
p = 0;
while (start <= end) {
arrs[start++] = temp[p++];
}
}
}
}