-
530.二叉搜索树的最小绝对差
力扣题目链接(opens new window)
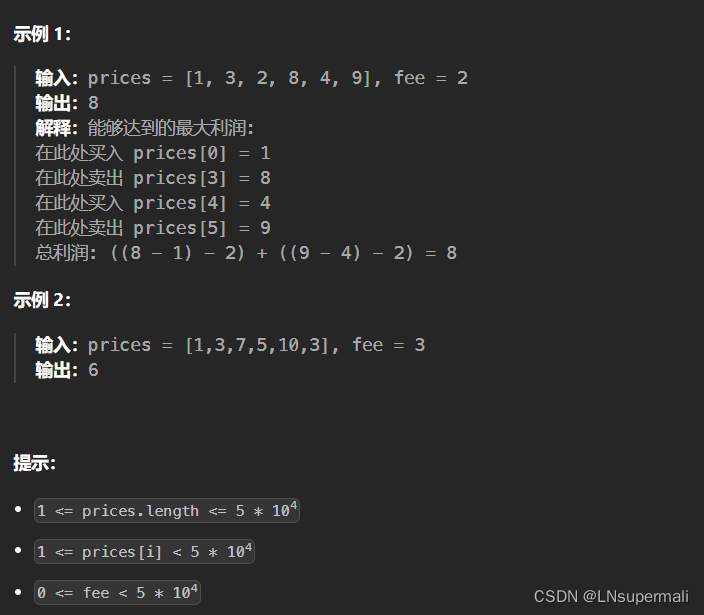
给你一棵所有节点为非负值的二叉搜索树,请你计算树中任意两节点的差的绝对值的最小值。
示例:

提示:树中至少有 2 个节点。
class Solution { TreeNode pre;// 记录上一个遍历的结点 int result = Integer.MAX_VALUE; public int getMinimumDifference(TreeNode root) { if(root==null)return 0; traversal(root); return result; } public void traversal(TreeNode root){ if(root==null)return; //左 traversal(root.left); //中 if(pre!=null){ result = Math.min(result,root.val-pre.val); } pre = root; //右 traversal(root.right); } }和day20的方法一样,利用二叉搜索树的特性,都是用双指针的形式,用pre指向前一个节点,用cur指向当前节点,然后比较取最小绝对差。
-
501.二叉搜索树中的众数
力扣题目链接(opens new window)
给定一个有相同值的二叉搜索树(BST),找出 BST 中的所有众数(出现频率最高的元素)。
假定 BST 有如下定义:
- 结点左子树中所含结点的值小于等于当前结点的值
- 结点右子树中所含结点的值大于等于当前结点的值
- 左子树和右子树都是二叉搜索树
-
例如:
给定 BST [1,null,2,2],

返回[2].
提示:如果众数超过1个,不需考虑输出顺序
-
class Solution { ArrayList<Integer> resList; int maxCount; int count; TreeNode pre; public int[] findMode(TreeNode root) { resList = new ArrayList<>(); maxCount = 0; count = 0; pre = null; findMode1(root); int[] res = new int[resList.size()]; for (int i = 0; i < resList.size(); i++) { res[i] = resList.get(i); } return res; } public void findMode1(TreeNode root) { if (root == null) { return; } findMode1(root.left); int rootValue = root.val; // 计数 if (pre == null || rootValue != pre.val) { count = 1; } else { count++; } // 更新结果以及maxCount if (count > maxCount) { resList.clear(); resList.add(rootValue); maxCount = count; } else if (count == maxCount) { resList.add(rootValue); } pre = root; findMode1(root.right); } }
该题与上道题思路一样,主要就是双指针的应用,要考虑好集合List的clear和add的情况,然后考虑所有情况即可解决。
-
236. 二叉树的最近公共祖先
力扣题目链接(opens new window)
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
例如,给定如下二叉树: root = [3,5,1,6,2,0,8,null,null,7,4]
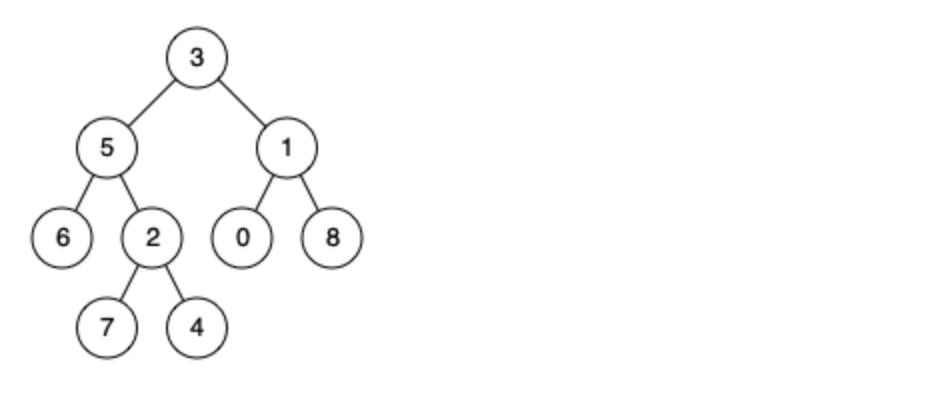
示例 1: 输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1 输出: 3 解释: 节点 5 和节点 1 的最近公共祖先是节点 3。
示例 2: 输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4 输出: 5 解释: 节点 5 和节点 4 的最近公共祖先是节点 5。因为根据定义最近公共祖先节点可以为节点本身。
说明:
- 所有节点的值都是唯一的。
- p、q 为不同节点且均存在于给定的二叉树中。
-
class Solution { public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) { if (root == null || root == p || root == q) { // 递归结束条件 return root; } // 后序遍历 TreeNode left = lowestCommonAncestor(root.left, p, q); TreeNode right = lowestCommonAncestor(root.right, p, q); if(left == null && right == null) { // 若未找到节点 p 或 q return null; }else if(left == null && right != null) { // 若找到一个节点 return right; }else if(left != null && right == null) { // 若找到一个节点 return left; }else { // 若找到两个节点 return root; } } }该题的关键是要考虑清楚遍历顺序(后序遍历),以及向上返回结果的思想,不光要考虑p、q在两个二叉树上的情况,还要考虑p是q的公共祖先这一情况,但是这个情况包含在else if情况里。