🌈个人主页:秦jh__https://blog.csdn.net/qinjh_?spm=1010.2135.3001.5343
🔥 系列专栏:《数据结构》https://blog.csdn.net/qinjh_/category_12536791.html?spm=1001.2014.3001.5482

目录
堆排序
第一种
编辑
第二种
TOP-K问题
建堆的时间复杂度
向下调整建堆的时间复杂度:
向上调整建堆的时间复杂度:
补充
前言
💬 hello! 各位铁子们大家好哇。
今日更新了堆排序,top-k问题和时间复杂度的内容
🎉 欢迎大家关注🔍点赞👍收藏⭐️留言📝
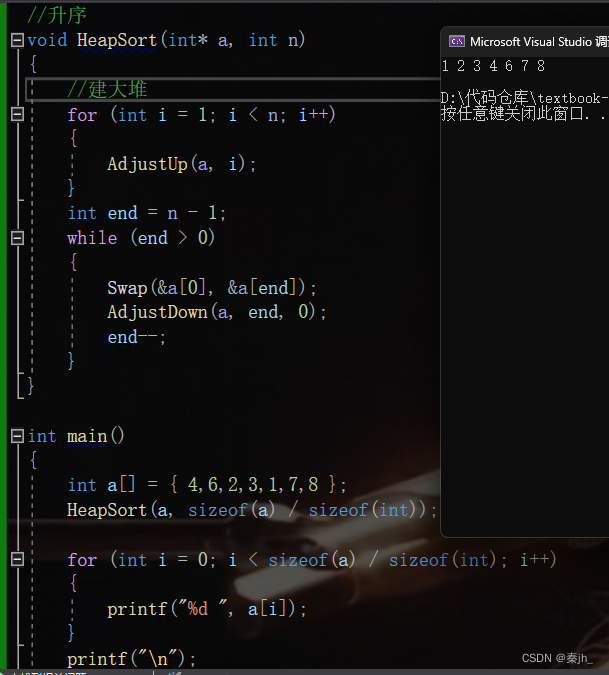
堆排序
第一种
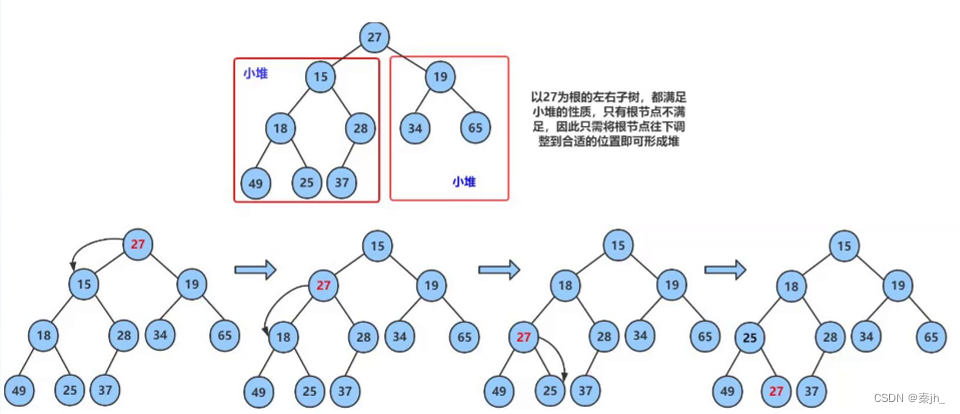
假如左右子树都是小堆,我们只需要进行向下调整建堆即可。
下方是建大堆:
思路分析:这里的向上和向下调整都是建大堆的。如果我们想进行升序排序,我们就得先建大堆。因为小堆的同一层中,无法进行比较。 接着,交换根结点和最后一个结点,这时就已经将最大的数排在末尾了。然后再从根结点向下调整建大堆,这时第二大的数就排在了根结点,再swap进行交换。end--表示不再对已排好的数进行操作。如此循环,即可进行升序。
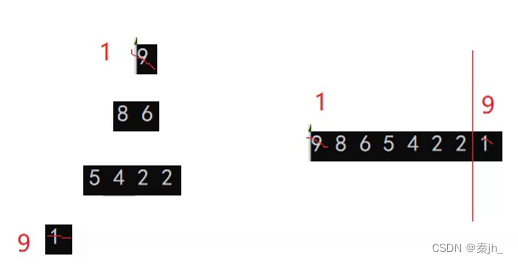
总结:如果是升序,就要建大堆。如果是降序,就要建小堆。 堆排序的本质是选择排序。
建堆的时间复杂度:N*logN
选数的时间复杂度:(N-1)*logN
第二种
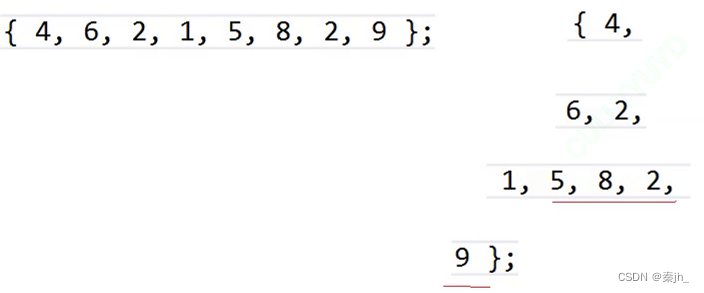
当左右子树不一定都是小堆时,我们就要进行从下往上的向下调整建堆。
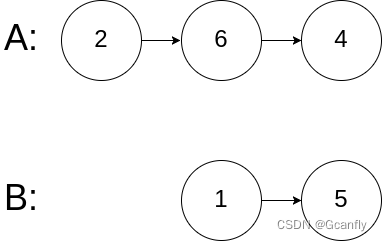
方法:从倒数第一个非叶子开始(即最后一个节点的父亲)。9,2,8,5不用调,我们从1开始,1和9满足小堆。接着往前一位数到2,此时也满足小堆。继续往前到6,1和5比,1更小,所以1和6交换。接着来到4,交换后的1和2,1更小,4就和1交换
此方法的时间复杂度是O(N),并且此方式只需要一个向下调整,不需要多写一个向上调整函数。
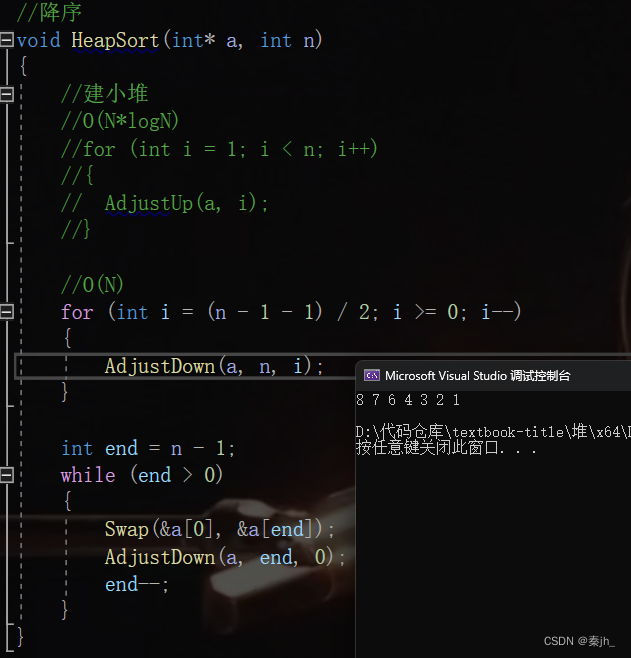
建小堆时,我们就会得到降序的数据。
TOP-K问题
TOP-K问题:即求数据结合中前K个最大的元素或者最小的元素,一般情况下数据量都比较大。
比如:专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。
对于Top-K问题,能想到的最简单直接的方式就是排序,但是:如果数据量非常大,排序就不太可取了(可能数据都不能一下子全部加载到内存中)。最佳的方式就是用堆来解决,基本思路如下:
1.用数据集合中前K个元素来建堆
- 前k个最大的元素,则建小堆
- 前k个最小的元素,则建大堆
2.用剩余的N-K个元素依次与堆顶元素来比较,不满足则替换堆顶元素
将剩余N-K个元素依次与堆顶元素比完之后,堆中剩余的K个元素就是所求的前K个最小或者最大的元素。
举例如下:
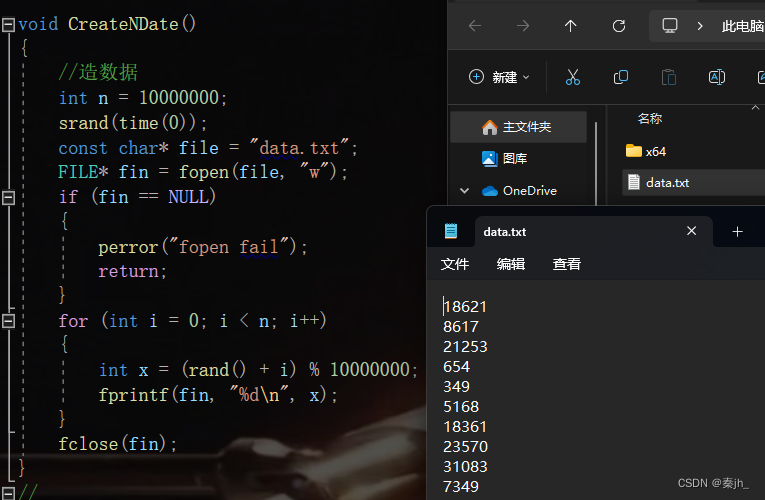
我们先生成一千万个随机数。
topk函数如下:
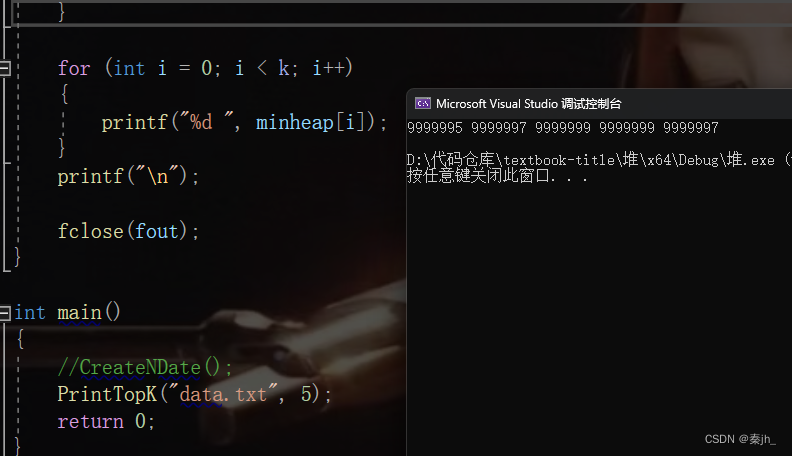
void PrintTopK(const char* file, int k)
{
FILE* fout = fopen(file, "r");
if (fout == NULL)
{
perror("fopen fail");
return;
}
//建一个k个数的小堆
int* minheap = (int*)malloc(sizeof(int) * k);
if (minheap == NULL)
{
perror("malloc fail");
return;
}
//读取前k个,建小堆
for (int i = 0; i < k;i++)
{
fscanf(fout, "%d", &minheap[i]);
AdjustUp(minheap, i);
}
int x = 0;
while (fscanf(fout, "%d", &x) != EOF)
{
if (x > minheap[0])
{
minheap[0] = x;
AdjustDown(minheap, k, 0);
}
}
for (int i = 0; i < k; i++)
{
printf("%d ", minheap[i]);
}
printf("\n");
fclose(fout);
}我们先建立k个数的小堆,并将前k个数放进去。接着从第k+1开始的数开始与根结点比较,如果大于,就替换,然后进行向下调整,恢复成堆的形式。直到所有的数都比较完,我们就能找出前k个最大或最小的数了。
最后的运行结果如下:
建堆的时间复杂度
向下调整建堆的时间复杂度:
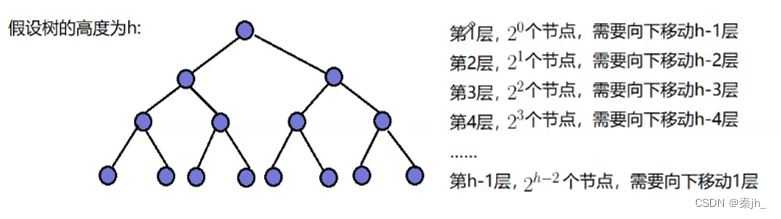
这里举例向下调整建堆的时间复杂度:
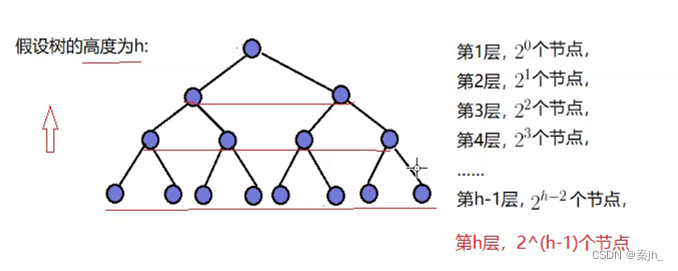
因为第h层是叶,就不需要向下移动了。具体计算过程如下图,因为是等差*等比,所以采用错位相减法进行计算。

因为最后的结果中的h是树的高度,不方便看出时间复杂度,替换成N(节点的个数)
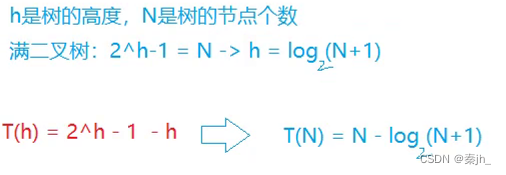
最终,时间复杂度是O(N)。
向上调整建堆的时间复杂度:
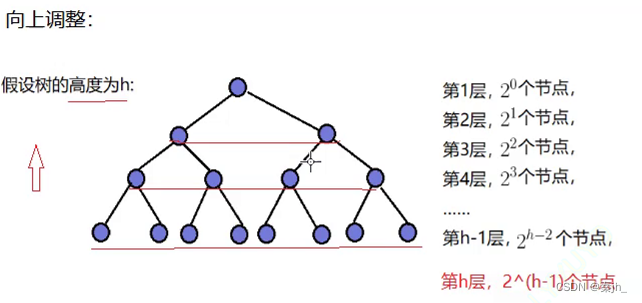


上方是求向上调整建堆时间复杂度的计算过程,原理与向下调整的一样。
最终的时间复杂度是:O(N*logN)
补充
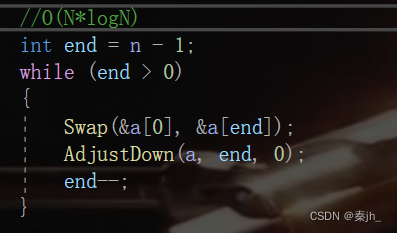
上方的过程的时间复杂度是O(N*logN),他跟上方的向上调整建堆相似,都是多*多,少*少的关系。因为最后一层有2^(h-1)个节点,每次交换后,最坏情况要向下调整(h-1)层,即多*多。第1层有一个节点,向下调整0层,即少*少。