一道有意思的图论题

news2024/11/17 3:28:06

今天写这道题的过程就一直在摆，主要是写不太出来，之前想到动态规划去了，然后又开始深搜，在出口那块放动态规划
题：
D. Ela and the Wiring Wizard
点我
但是cf让我明白了一个道理，任何一道我写不出来的题代码不会超过50行，嘤（的确，太长的也不太好调试，这样的题显然不是模拟，要推出一些结论，然后往上整
这个题的大意是 $u_{i},v_{i},t_{i}$ 通过 $v_{i}$ 相连，那么可以花费 $u_{i},v_{i}$ 之间的权重把这两条边断开，然后把 $u_{i},t_{i}$ 连在一起，这样的话走 $u_{i},t_{i}$ 就可以使用 $u_{i},v_{i}$ 之间的权重了。这样的操作可以进行任意多次，求最后从 $1\rightarrow n$ 的最小花费是多少，把消边的时间也要算上。
现在看来，我的做法的确很沙雕。我的错误在于，我是深搜出一条从 $1$ 到 $n$ 的路径，然后把这条路径动规，但是这里面有一个问题就是，如果一开始的一条路径不能从 $1$ 走到 $n$ ，这条路径也有可能通过操作最短。
你看这个图，他的答案是 $154$ ，为啥，我当时还在想是 $43 ， 54$ 怎么组合，因为我算的一直都是 $162$ ，后来我才明白，他一直在用 $22$ 那条边来回倒。
你可以
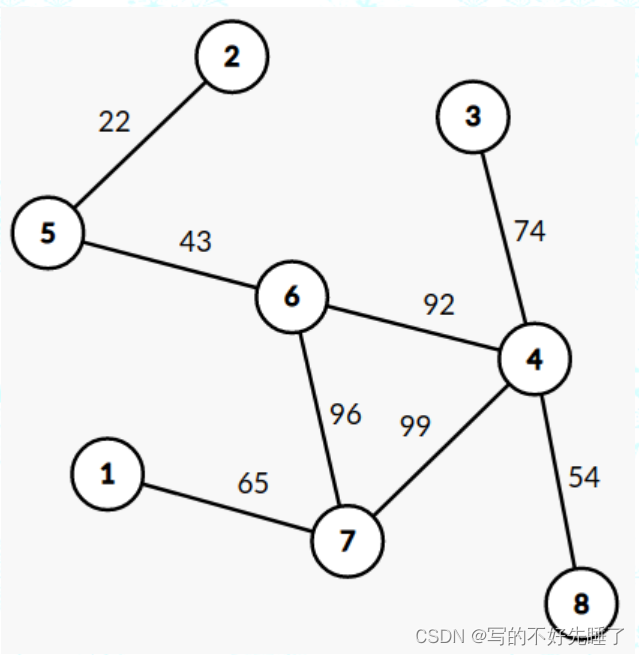
在这里插入图片描述
比如这个图首先 $2$ 通过 $5$ 连到 $4$ 上，花费 $2$ 个 $22$ ，然后 $4$ 通过 $2$ 连到 $4$ 上，花费 $1$ 个 $22$ ，然后， $4$ 通过 $4$ 连到 $1$ 上花费 $2$ 个 $22$ ，然后 $1$ 通过 $4$ 连到 $8$ 上，花费 $1$ 个 $22$ ，最后从 $1$ 走到 $8$ 花费 $1$ 个 $22$
这种是间接连接， $u$ 和 $v$ 之间的连边变化情况：走 $v$ 到 $i$ 个路径让 $u$ 连到 $i$ 上，然后 $v$ 和 $i$ 相连之后，让 $i$ 和 $i$ 形成自环，然后让 $i$ 和 $1$ 与 $n$ 连接，花费 $i$ 到 $1$ 和 $i$ 到 $n$ 的路径。最后再走一条边（运行时）
直接连接： $u$ 先连到 $1$ ，然后 $1$ 再连到 $n$ ： $u$ 连到 $1$ 走的时 $v$ 到1的路径然后 $1$ 连到 $n$ 走的是 $u$ 到 $n$ 的路径，画个图就知道了
所以方程是：

// direct connect
		ans = min(ans, 1LL * w * (f[0][u] + f[v][n-1] + 1));
		ans = min(ans, 1LL * w * (f[0][v] + f[u][n-1] + 1));
		
		// indirect connect
		for (int k = 0; k < n; ++k) {
			ans = min(ans, 1LL * w * (f[v][k] + 1 + f[k][0] + f[k][n-1] + 1));
			ans = min(ans, 1LL * w * (f[u][k] + 1 + f[k][0] + f[k][n-1] + 1));
		}

以上思路参考文章：
参考文章
(AC代码）：

#include<iostream>
#include<cstdio>
#include<vector>
using namespace std;
#define min(a,b) ((a<b)?a:b)
typedef long long ll;
const int length = 505;
vector<pair<int, pair<int, int>>> edge;
int f[length][length];
int main(void)
{
	int t;
	scanf_s("%d", &t);
	for (int i = 0; i < t; i++)
	{
		edge.clear();
		int n, m;
		scanf_s("%d%d", &n, &m);
		for (int i = 1; i <= n; i++)
		{
			for (int j = 1; j <= n; j++)
			{
				if (i == j)f[i][j] = 0;
				else f[i][j] = INT_MAX>>1;
			}
		}
		for (int i = 0; i < m; i++)
		{
			int a, b, c;
			scanf_s("%d%d%d", &a, &b, &c);
			edge.push_back({ a,{b,c} });
			f[a][b] = 1;
			f[b][a] = 1;
		}
		for (int k = 1; k <= n; k++)
		{
			for (int i = 1; i <= n; i++)
			{
				for (int j = 1; j <= n; j++)
				{
					f[i][j] = min(f[i][j], f[i][k] + f[k][j]);
				}
			}
		}
		ll ans = LLONG_MAX;
		for (int i = 0; i < m; i++)
		{
			int u = edge[i].first;
			int v = edge[i].second.first;
			int w = edge[i].second.second;
			//直接
			ans = min(ans, (ll)w*(f[u][1] + f[v][n] + 1));
			ans = min(ans, (ll)w*(f[v][1] + f[u][n] + 1));

			//间接
			for (int i = 1; i <= n; i++)
			{
				ans = min(ans, (ll)w*(f[u][i] + 1 + f[i][1] + f[i][n] + 1));
				ans = min(ans, (ll)w*(f[v][i] + 1 + f[i][1] + f[i][n] + 1));
			}
		}
		printf("%lld\n", ans);
	}
}

我写的沙雕代码：

#include<iostream>
#include<cstdio>
#include<vector>
#define min(a,b) ((a<b)?a:b)
using namespace std;
typedef long long ll;
class s
{
public:
	ll weight;
	ll cost;
	s()
	{

	}
	s(int yh)
	{
		weight = yh;
		cost = 0;
	}
	ll operator +( s a)
	{
		return 2*weight + cost + a.cost;
	}
	 
};

const int length = 505;
struct s linjie[length][length];
bool flag[length][length];
ll dp[length][length];
vector<int> s1;
vector<vector<int>> edge(length);
int vis[length];
int n;
ll res = LLONG_MAX;
void dfs(int cur, int fa)
{
	if (cur == n)
	{
		int yh1 = s1.size();
		for (int length = 2; length <yh1; length++)
		{
			for (int i = 0; i <yh1 - length; i++)
			{
				int j = i + length;
				int u = s1[i];
				int v = s1[j];
				ll yh = min(dp[u][v],linjie[u][v].weight+linjie[u][v].cost);//这个yh草率了
				for (int k = 1; k <= n; k++)
				{
					//if (!(flag[u][k] && flag[k][v]))continue;
					if ((linjie[u][k] + linjie[k][v] )< yh&&linjie[k][v].weight!=INT_MAX>>1)
					{
						linjie[u][v].weight = linjie[v][u].weight=linjie[u][k].weight;
						linjie[u][v].cost = linjie[v][u].cost=linjie[u][k].cost + linjie[k][v].cost+linjie[u][k].weight;
						
					}
					if ((linjie[v][k] + linjie[k][u]) < yh&&linjie[k][u].weight!=INT_MAX>>1)
					{
						linjie[u][v].weight = linjie[v][u].weight = linjie[v][k].weight;
						linjie[u][v].cost = linjie[v][u].cost = linjie[v][k].cost + linjie[k][u].cost+linjie[v][k].weight;
					}
				}
			}
		}
		res = min(res, linjie[1][n].weight+linjie[1][n].cost);
		return;
	}
	for (int i=1;i<=n;i++)
	{
		int v = i;
		if (!vis[v] && v != fa&&flag[cur][v])
		{
			s1.push_back(v);
			vis[v] = 1;
			dfs(v, cur);
			s1.pop_back();
			vis[v] = 0;
		}
	}
}
int main(void)
{
	int t;
	scanf_s("%d", &t);
	for (int i = 0; i < t; i++)
	{
		int m;
		scanf_s("%d%d", &n, &m);
		res = LLONG_MAX;
		for (int i = 1; i <= n; i++)
		{
			for (int j = 1; j <= n; j++)
			{
				linjie[i][j].weight = INT_MAX>>1;
				linjie[i][j].cost = 0;
				dp[i][j] = INT_MAX >> 1;
			}
		}
		for (int i = 0; i < m; i++)
		{
			int a, b, c;
			scanf_s("%d%d%d", &a, &b, &c);
			linjie[a][b].weight = min(linjie[a][b].weight,c);
			linjie[b][a].weight = min(linjie[b][a].weight,c);
			flag[a][b] = 1;
			flag[b][a] = 1;
			dp[a][b] = min(dp[a][b],c);
			dp[b][a] = min(dp[b][a],c);
		}
		for (int k = 1; k <= n; k++)
		{
			for (int i = 1; i <= n; i++)
			{
				for (int j = 1; j <= n; j++)
				{
					dp[i][j] = min(dp[i][j], dp[i][k] + dp[k][j]);
				}
			}
		}
		vis[1] = 1;
		s1.push_back(1);
		for(int i=n-1;i>=1;i--)
	     	dfs(i, -1);
		printf("%lld\n", min(dp[1][n],res));
	}
}