数据结构排序二叉树(下)

news2024/11/16 17:59:28

哎,调了几天深度学习模型,今天来更新排序二叉树

文章目录

前言

一、排序二叉树的结构定义

二、在排序二叉树添加数据

三、定义创建排序二叉树函数

四、查找一棵二叉排序树中的结点x的所在层数

五、删除二叉排序树中T关键字x的节点

六、查找二叉排序树中的所有小于key的关键字

七、已知二叉排序中每个节点值为整形,采用二叉链表存储,编写算法删除二叉排序树中所有关键字小于x的

八.总结与验证

前言

排序二叉树就这几个习题了,但实际上还有更难得几道习题,因为实现起来真的难,而且在使用中也难用到所以就给大家几道简单的例子,帮助大家来熟悉.

一、排序二叉树的结构定义

typedef int ElemType;
//二叉排序树左>根>右,树中没有重复值
//二叉排序树的数据结构
typedef struct BSTNode {
	ElemType data;//数据节点类型为int
	struct BSTNode* lchild;
	struct BSTNode* rchild;
}BSTNode,*BSTree;

其实就是二叉树的数据结构只是对树中节点数据有约束.

二、在排序二叉树添加数据

//插入节点函数
void insertNode(BSTree& T, ElemType e) {
	if (T == NULL) {//找到合适的位置插入节点
		BSTNode* pNode = (BSTNode*)malloc(sizeof(BSTNode));
		assert(pNode);
		pNode->data = e;
		pNode->lchild = NULL;
		pNode->rchild = NULL;
		T = pNode;//别忘了链接上
	}
	else if (T->data > e) {//插入左子树
		insertNode(T->lchild, e);
	}
	else if (T->data < e) {//插入右子树
		insertNode(T->rchild, e);
	}
}

由于二叉树左>根>右所以在构建二叉树使需要满足要求.

算法思想:运用递归思想,将待插入数据与当前节点比较如果小于当前节点数据表明插入数据应插在当前节点的左子树,反之当如果插入数据比当前的节点数据大,则表明插入数据应插到当前数据的右子树,直到遇到空节点表示找到插入位置,申请节点插入即可.

三、定义创建排序二叉树函数

//定义创建二叉排序树函数
BSTNode* creatBSTree() {
	BSTNode* T = NULL;
	ElemType enternum = 999999;//999999表示退出输入
	printf("请输入序列(以999999作为结束标志):");
	while (scanf("%d", &enternum) && enternum != 999999) {
		insertNode(T, enternum);
	}
	return T;
}

就依次插入节点就可以了.

四、查找一棵二叉排序树中的结点x的所在层数

//例1:查找一棵二叉排序树中的结点x的所在层数
int nodelevel(BSTree T, int level,ElemType x) {
	if (T == NULL) {//没找到返回0
		return 0;
	}
	else if (T->data > x) {//左子树寻找
		return nodelevel(T->lchild, level+1, x);
	}
	else if (T->data < x) {//右子树寻找
		return nodelevel(T->rchild, level+1, x);
	}
	else {
		return level;//返回层次
	}
}

算法思想:采用递归的形式,但传参时传入一个层数,找到返回即可,注意这里层数是值传递,不是址传递.

五、删除二叉排序树中T关键字x的节点

//例2:删除二叉排序树中T关键字x的节点
//算法思想:首先找到节点x此时就要分情况讨论(1)节点既没有左孩子又没有右孩子,直接删去节点并将指针制空;
//(2)节点只有左孩子(或只有右孩子),指针指向左孩子(右孩子)并删除节点;
//(3)节点既有左孩子又有右孩子,此时有两种处理方案1.找到左子树的最大节点将右孩子链接到最大节点的右指针
//2.找到右子树的最小节点,将左孩子链接到最小节点的左指针
void deleteOperation(BSTree& T) {
	if (T == NULL) return;
	if (T->lchild == NULL && T->rchild == NULL) {
		free(T);
		T = NULL;
	}
	else if (T->lchild != NULL && T->rchild == NULL) {
		BSTNode* tmp = T;
		T = T->lchild;
		free(tmp);
		tmp = NULL;
	}
	else if (T->lchild == NULL && T->rchild != NULL) {
		BSTNode* tmp = T;
		T = T->rchild;
		free(tmp);
		tmp = NULL;
	}
	else {//既有左孩子又有右孩子
		BSTNode* pMaxnode = T->lchild;
		while (pMaxnode->rchild != NULL) {
			pMaxnode = pMaxnode->rchild;
		}
		pMaxnode->rchild = T->rchild;
		BSTNode* tmp = T;
		T = T->lchild;
		free(tmp);
		tmp = NULL;
	}
}
//查找并删除节点
void deletenode(BSTree &T,ElemType x) {
	if (T != NULL) {
		if (T->data == x) {
			deleteOperation(T);
		}
		else if (T->data < x) {
			deletenode(T->rchild, x);
		}
		else {
			deletenode(T->lchild, x);
		}
	}

}

这个算法还有一个思想就是找到左子树最大的节点复制到删除节点上,递归在左子树删除左子树最大节点.

字有点丑见谅.

六、查找二叉排序树中的所有小于key的关键字

//例3:查找二叉排序树中的所有小于key的关键字
void getSmallerkey(BSTree T, ElemType key) {
	if (T != NULL) {
		getSmallerkey(T->lchild, key);
		if (T->data < key) {
			printf("%d ", T->data);
			getSmallerkey(T->rchild, key);
		}
	}
}

七、已知二叉排序中每个节点值为整形,采用二叉链表存储,编写算法删除二叉排序树中所有关键字小于x的

//例4:已知二叉排序中每个节点值为整形,采用二叉链表存储,编写算法删除二叉排序树中所有关键字小于x的节点
//定义递归删除树函数
void deleteFunc(BSTree& T) {//递归删除树
	if (T != NULL) {
		deleteFunc(T->lchild);
		deleteFunc(T->rchild);
		free(T);
		T = NULL;
	}
}
//定义删除小于x节点的函数(采用先序遍历的思想)
void deleteSmallernode(BSTree &T,ElemType x) {
	if (T != NULL) {
		if (T->data == x) {//根节点等于x说明左子树都小于x递归删除
			deleteFunc(T->lchild);
		}
		else if (T->data < x) {//根节点小于x左子树均小于x,删除根节点在递归删除右子树小于x的节点
			deleteFunc(T->lchild);
			BSTNode* tmp = T;
			T = T->rchild;
			free(tmp);
			tmp = NULL;
			deleteSmallernode(T, x);
		}
		else {//根节点大于x递归删除左子树小于x的节点
			deleteSmallernode(T->lchild, x);
		}
	}
}

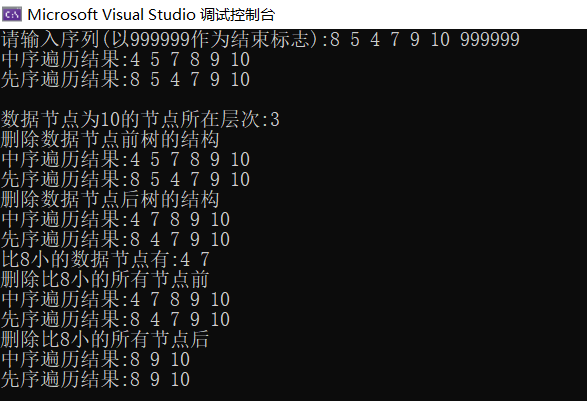
八.总结与验证

#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<malloc.h>
#include<assert.h>
typedef int ElemType;
//二叉排序树左>根>右,树中没有重复值
//二叉排序树的数据结构
typedef struct BSTNode {
	ElemType data;//数据节点类型为int
	struct BSTNode* lchild;
	struct BSTNode* rchild;
}BSTNode,*BSTree;
//插入节点函数
void insertNode(BSTree& T, ElemType e) {
	if (T == NULL) {//找到合适的位置插入节点
		BSTNode* pNode = (BSTNode*)malloc(sizeof(BSTNode));
		assert(pNode);
		pNode->data = e;
		pNode->lchild = NULL;
		pNode->rchild = NULL;
		T = pNode;//别忘了链接上
	}
	else if (T->data > e) {//插入左子树
		insertNode(T->lchild, e);
	}
	else if (T->data < e) {//插入右子树
		insertNode(T->rchild, e);
	}
}
//定义创建二叉排序树函数
BSTNode* creatBSTree() {
	BSTNode* T = NULL;
	ElemType enternum = 999999;//999999表示退出输入
	printf("请输入序列(以999999作为结束标志):");
	while (scanf("%d", &enternum) && enternum != 999999) {
		insertNode(T, enternum);
	}
	return T;
}
//中序遍历二叉排序树
void inorderTraverse(BSTree T) {
	if (T != NULL) {
		inorderTraverse(T->lchild);
		printf("%d ", T->data);
		inorderTraverse(T->rchild);
	}
}
//先序遍历二叉排序树
void preorderTraverse(BSTree T) {
	if (T != NULL) {
		printf("%d ", T->data);
		preorderTraverse(T->lchild);
		preorderTraverse(T->rchild);
	}
}
//遍历二叉排序树(先,中)
void Traverse(BSTree T) {//这函数主要是用来验证
	printf("中序遍历结果:");
	inorderTraverse(T);
	printf("\n");
	printf("先序遍历结果:");
	preorderTraverse(T);
	printf("\n");
}
//例1:查找一棵二叉排序树中的结点x的所在层数
int nodelevel(BSTree T, int level,ElemType x) {
	if (T == NULL) {//没找到返回0
		return 0;
	}
	else if (T->data > x) {//左子树寻找
		return nodelevel(T->lchild, level+1, x);
	}
	else if (T->data < x) {//右子树寻找
		return nodelevel(T->rchild, level+1, x);
	}
	else {
		return level;//返回层次
	}
}
//例2:删除二叉排序树中T关键字x的节点
//算法思想:首先找到节点x此时就要分情况讨论(1)节点既没有左孩子又没有右孩子,直接删去节点并将指针制空;
//(2)节点只有左孩子(或只有右孩子),指针指向左孩子(右孩子)并删除节点;
//(3)节点既有左孩子又有右孩子,此时有两种处理方案1.找到左子树的最大节点将右孩子链接到最大节点的右指针
//2.找到右子树的最小节点,将左孩子链接到最小节点的左指针
void deleteOperation(BSTree& T) {
	if (T == NULL) return;
	if (T->lchild == NULL && T->rchild == NULL) {
		free(T);
		T = NULL;
	}
	else if (T->lchild != NULL && T->rchild == NULL) {
		BSTNode* tmp = T;
		T = T->lchild;
		free(tmp);
		tmp = NULL;
	}
	else if (T->lchild == NULL && T->rchild != NULL) {
		BSTNode* tmp = T;
		T = T->rchild;
		free(tmp);
		tmp = NULL;
	}
	else {//既有左孩子又有右孩子
		BSTNode* pMaxnode = T->lchild;
		while (pMaxnode->rchild != NULL) {
			pMaxnode = pMaxnode->rchild;
		}
		pMaxnode->rchild = T->rchild;
		BSTNode* tmp = T;
		T = T->lchild;
		free(tmp);
		tmp = NULL;
	}
}
//查找并删除节点
void deletenode(BSTree &T,ElemType x) {
	if (T != NULL) {
		if (T->data == x) {
			deleteOperation(T);
		}
		else if (T->data < x) {
			deletenode(T->rchild, x);
		}
		else {
			deletenode(T->lchild, x);
		}
	}

}
//例3:查找二叉排序树中的所有小于key的关键字
void getSmallerkey(BSTree T, ElemType key) {
	if (T != NULL) {
		getSmallerkey(T->lchild, key);
		if (T->data < key) {
			printf("%d ", T->data);
			getSmallerkey(T->rchild, key);
		}
	}
}
//例4:已知二叉排序中每个节点值为整形,采用二叉链表存储,编写算法删除二叉排序树中所有关键字小于x的节点
//定义递归删除树函数
void deleteFunc(BSTree& T) {//递归删除树
	if (T != NULL) {
		deleteFunc(T->lchild);
		deleteFunc(T->rchild);
		free(T);
		T = NULL;
	}
}
//定义删除小于x节点的函数(采用先序遍历的思想)
void deleteSmallernode(BSTree &T,ElemType x) {
	if (T != NULL) {
		if (T->data == x) {//根节点等于x说明左子树都小于x递归删除
			deleteFunc(T->lchild);
		}
		else if (T->data < x) {//根节点小于x左子树均小于x,删除根节点在递归删除右子树小于x的节点
			deleteFunc(T->lchild);
			BSTNode* tmp = T;
			T = T->rchild;
			free(tmp);
			tmp = NULL;
			deleteSmallernode(T, x);
		}
		else {//根节点大于x递归删除左子树小于x的节点
			deleteSmallernode(T->lchild, x);
		}
	}
}
int main() {
	//创建一棵二叉排序树
	//8 5 4 7 9 10 999999
	BSTree T = creatBSTree();
	Traverse(T);
	printf("\n");
	int a = 10;
	printf("数据节点为%d的节点所在层次:%d\n", a,nodelevel(T, 1, a));
	printf("删除数据节点前树的结构\n");
	Traverse(T);
	deletenode(T, 5);
	printf("删除数据节点后树的结构\n");
	Traverse(T);
	printf("比8小的数据节点有:");
	getSmallerkey(T, 8);
	printf("\n");
	int b = 8;
	printf("删除比%d小的所有节点前\n",b);
	Traverse(T);
	deleteSmallernode(T, b);
	printf("删除比%d小的所有节点后\n", b);
	Traverse(T);
	return 0;
}

兄弟们马上要到图啦,最有意思的一部分要到啦.加油哦

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1390772.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

QT上位机开发（动画效果）

QT上位机开发（动画效果）

【 声明&#xff1a;版权所有&#xff0c;欢迎转载&#xff0c;请勿用于商业用途。 联系信箱&#xff1a;feixiaoxing 163.com】 不管是仿真&#xff0c;还是对真实环境的一比一模拟&#xff0c;动画都是非常好的一种呈现方式。目前在qt上面&#xff0c;实现动画主要有两种方法…
阅读更多...
Github项目推荐--MusicFreeDesktop

Github项目推荐--MusicFreeDesktop

项目地址 https://github.com/maotoumao/MusicFreeDesktop 项目简述 这是一个开源的音乐播放器&#xff0c;主要使用typescript编写&#xff0c;页面很漂亮。支持自定义主题和插件化配置音源&#xff0c;是一大亮点。 项目截图
阅读更多...
【论文阅读】Latent Consistency Models (LDMs)、LCM-LoRa

【论文阅读】Latent Consistency Models (LDMs)、LCM-LoRa

文章目录 IntroductionPreliminariesDiffusion ModelsConsistency Models Latent Consistency ModelsConsistency Distillation in the Latent SpaceOne-Stage Guided Distillation by Solving Augmented PF-ODEAccelerating Distillation with Skipping Time StepsLatent Cons…
阅读更多...
Rust-数组

Rust-数组

数组是一个容器&#xff0c;它在一块连续空间内存中&#xff0c;存储了一系列的同样类型的数据。 数组中元素的占用空间大小必须是编译期确定的。 数组本身所容纳的元素个数也必须是编译期确定的&#xff0c;执行阶段不可变。 如果需要使用变长的容器&#xff0c;可以使用标…
阅读更多...
如何使用程序控制微信发送消息

如何使用程序控制微信发送消息

简介 使用杨中科老师的nuget包NetAutoGUI&#xff0c;控制微信给指定用户发送消息&#xff0c;如果想下面视频一样使用此功能用来轰炸朋友&#xff0c;可以直接跳到最后一节&#xff0c;或者直接下载我的打包好的程序集 【免费】控制微信发送消息的程序资源-CSDN文库 微信轰炸…
阅读更多...
复合机器人作为一种新型的智能制造装备高效、精准和灵活的生产方式

复合机器人作为一种新型的智能制造装备高效、精准和灵活的生产方式

随着汽车制造业的快速发展&#xff0c;对于高效、精准和灵活的生产方式需求日益增强。复合机器人作为一种新型的智能制造装备&#xff0c;以其独特的优势在汽车制造中发挥着越来越重要的作用。因此&#xff0c;富唯智能顺应时代的发展趋势&#xff0c;研发出了ICR系列的复合机器…
阅读更多...
定岗定编：国有电力企业精细化管理改革方案

定岗定编：国有电力企业精细化管理改革方案

某发电厂作为神华国华集团下属单位&#xff0c;位于环渤海地区&#xff0c;成立于20世纪90年代&#xff0c;是国家“八五”、“九五”期间重点电力建设项目。在建立之初&#xff0c;公司引入了两台800MW超临界燃煤机组&#xff0c;总投资超过100亿元&#xff0c;近年开展了二期…
阅读更多...
RTSP协议实现发送ACC音频数据

RTSP协议实现发送ACC音频数据

一.AAC音频格式介绍 AAC音频格式&#xff1a;Advanced Audio Coding&#xff08;高级音频解码&#xff09;&#xff0c;是一种由MPEG—4标准定义的有损音频压缩格式。音频压缩编码的输出码流&#xff0c;以音频帧的形式存在。每个音频帧包含若干个音频采样的压缩数据&#xff0…
阅读更多...
Butler for Mac 菜单栏快速启动工具

Butler for Mac 菜单栏快速启动工具

Butler介绍 Butler for Mac版是一款Mac菜单栏快速启动工具&#xff0c;主要用于加速您的工作流程并简化您的日常任务。 借助Butler的帮助&#xff0c;您可以控制iTunes&#xff0c;启动应用程序&#xff0c;打开文件和文档&#xff0c;在用户之间切换&#xff0c;搜索网络等等…
阅读更多...
鸿蒙Harmony-列表组件（List）详解

鸿蒙Harmony-列表组件（List）详解

不要和别人比生活&#xff0c;每个人阶段不同&#xff0c;追求不同&#xff0c;活法自然也不同。只要今天的你能比昨天的你快乐一点点&#xff0c;那你就是自己人生赢家。 目录 一&#xff0c;定义 二&#xff0c;布局与约束 2.1 布局 2.2 约束 三&#xff0c;开发布局 3.1 设置…
阅读更多...
基于Python的汽车信息爬取与可视化分析系统

基于Python的汽车信息爬取与可视化分析系统

介绍 这款汽车信息网站是基于多项技术和框架设计的全面的汽车信息展示及查询系统。其中&#xff0c;采用了Python Django框架和Scrapy爬虫技术实现数据的抓取和处理&#xff0c;结合MySQL数据库进行数据存储和管理&#xff0c;利用Vue3、Element-Plus、ECharts以及Pinia等前端…
阅读更多...
【大数据】Flink 详解（九）：SQL 篇 Ⅱ

【大数据】Flink 详解（九）：SQL 篇 Ⅱ

《Flink 详解》系列&#xff08;已完结&#xff09;&#xff0c;共包含以下 10 10 10 篇文章&#xff1a; 【大数据】Flink 详解&#xff08;一&#xff09;&#xff1a;基础篇【大数据】Flink 详解&#xff08;二&#xff09;&#xff1a;核心篇 Ⅰ【大数据】Flink 详解&…
阅读更多...
Codeforces Round 920 (Div. 3)

Codeforces Round 920 (Div. 3)

Codeforces Round 920 (Div. 3) Codeforces Round 920 (Div. 3) A. Square 题意&#xff1a;随机给出正方形在平面坐标系上的四个顶点的坐标&#xff0c;求正方形的面积&#xff0c;正方形边与xy轴平行。 思路&#xff1a;因为正方形与坐标轴平行&#xff0c;所以找出相同的…
阅读更多...
React Native 原生组件回调JS层方法和 JS 层调用原生组件的事件方法

React Native 原生组件回调JS层方法和 JS 层调用原生组件的事件方法

一、原生组件回调 JS 层提供的事件方法 比如 TextInput 组件 onChangeText 属性&#xff0c;输入事件是发生在原生层的但是需要通知 JS 层发生了变化&#xff0c;并执行 JS 层的方法。 1、给原生组件添加一个按钮用于触发原生事件方法 在 XML 中添加一个按钮 为了方便让 Inf…
阅读更多...
已解决：g++: error: unrecognized command line option ‘-Wnull-dereference‘

已解决：g++: error: unrecognized command line option ‘-Wnull-dereference‘

VS运行正常的c代码&#xff0c;出现错误&#xff1a; 正在执行任务: C:/Windows/System32/cmd.exe /d /c g -Wall -Wextra -Wpedantic -Wshadow -Wformat2 -Wcast-align -Wconversion -Wsign-conversion -Wnull-dereference -g3 -O0 -c e:\Desktop\C\hdu\1000.cpp -o .\build\…
阅读更多...
保姆级ESP-IDF开发环境搭建

保姆级ESP-IDF开发环境搭建

1. 手动安装工具链&#xff0c;命令行方式&#xff08;windows&#xff09; 1.1 下载离线安装器 进入乐鑫 ESP-IDF Windows Installer Download 下载页面&#xff0c;选择离线版本工具&#xff08;网络原因&#xff0c;安装过程中使用github下载会出问题&#xff09;。 1.2 使…
阅读更多...
unity C#中使用ref、out区别和使用案例

unity C#中使用ref、out区别和使用案例

文章目录 ref 关键字out 关键字 在Unity&#xff08;以及C#编程语言中&#xff09;&#xff0c; ref 和 out 都是用来传递参数的引用&#xff0c;这意味着它们允许函数修改实参变量&#xff0c;并且这些修改会反映到调用函数的地方。但它们之间确实存在一些关键区别和使用场景…
阅读更多...
Flutter开发进阶之并发操作数据库

Flutter开发进阶之并发操作数据库

Flutter开发进阶之并发操作数据库 尽管 Flutter 本身不包含任何数据库功能&#xff0c;但可以使用各种第三方库和插件来在 Flutter 应用程序中实现数据库功能&#xff1b; 以下将使用sqflite作为例子&#xff0c;sqflite允许在 Flutter 应用程序中执行 SQL 查询&#xff0c;创…
阅读更多...
【干货】深入剖析冒泡排序算法：原理、步骤与复杂度分析

【干货】深入剖析冒泡排序算法：原理、步骤与复杂度分析

导语&#xff1a; 排序算法是计算机科学中的重要基础知识&#xff0c;而冒泡排序是最简单、最基础的排序算法之一。虽然冒泡排序的效率相对较低&#xff0c;但它的实现简单易懂&#xff0c;是理解排序算法的入门之选。本文将深入剖析冒泡排序算法的原理、步骤以及时间复杂度分析…
阅读更多...
vue 渲染数组，拖拽排序，渲染同一个数组拖拽排序不影响其他选中行状态

vue 渲染数组，拖拽排序，渲染同一个数组拖拽排序不影响其他选中行状态

当我们能够设置单行状态改变的时候&#xff0c;那么肯定可以拿到选中的当前行的id或者下标index。 只要设定一个初始化值在拖拽开始的时候重新赋值&#xff0c;然后再处理选中状态的时候进行判断即可。 前期写的时候没有注意到这个问题&#xff0c;可以看这个文章。 在复测的时…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023