坚持刷题,老年痴呆追不上我,今天先刷个简单的:翻转二叉树
题目
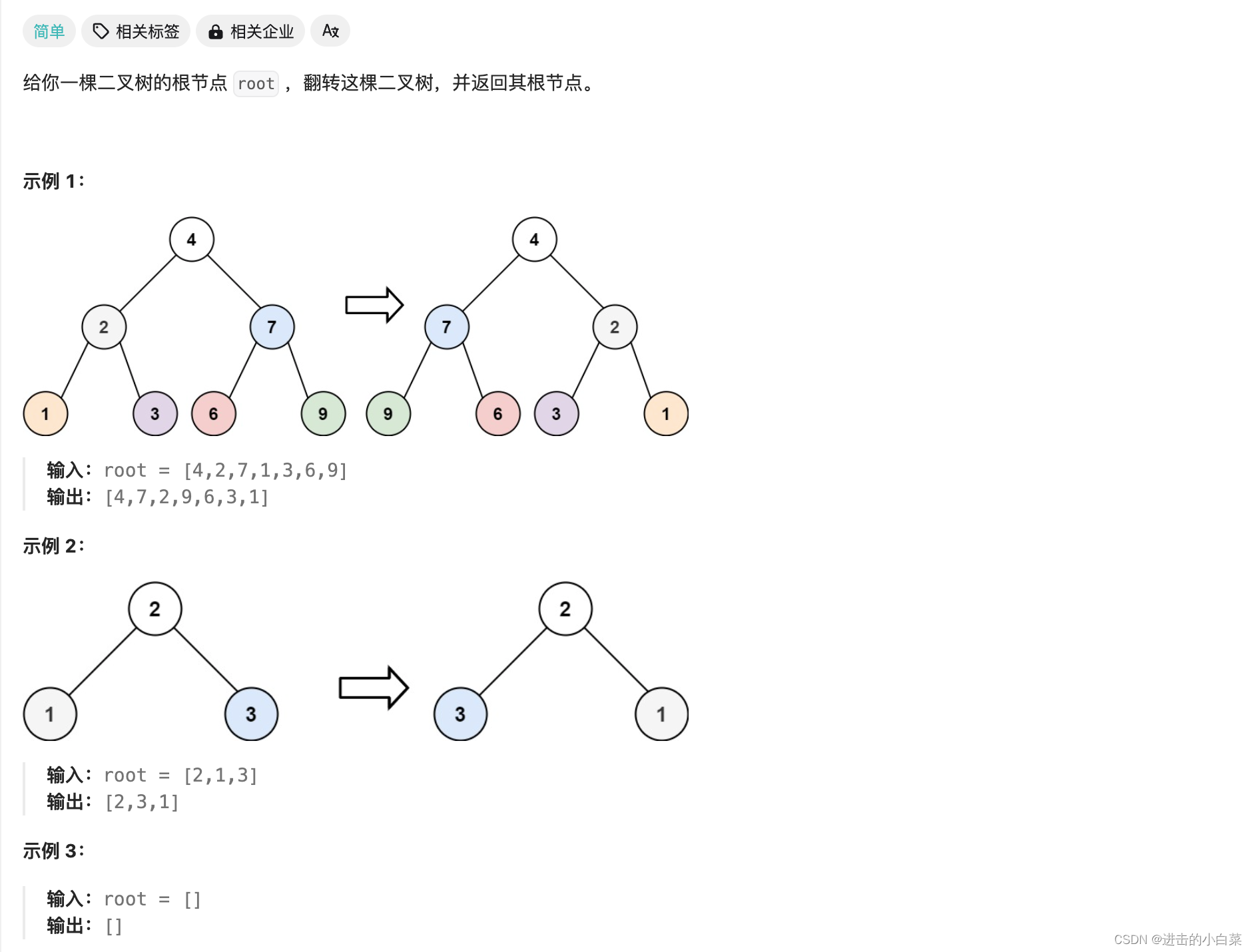
226.翻转二叉树
考察点
翻转二叉树又称为镜像二叉树,使用Java实现翻转二叉树通常是为了考察对二叉树的基本操作和递归的理解能力
- 递归的理解: 能够理解并实现递归的思想,将问题拆分为更小的子问题
- 二叉树的基本操作: 能够理解二叉树的节点结构,能够对节点进行访问和修改
- 边界条件的处理: 能够考虑到空树的情况,避免出现空指针异常
代码实现
class TreeNode {
int val;
TreeNode left;
TreeNode right;
public TreeNode(int val) {
this.val = val;
}
}
public class BinaryTreeInversion {
public TreeNode invertTree(TreeNode root) {
if (root == null) {
return null;
}
// 递归地翻转左右子树
TreeNode temp = root.left;
root.left = invertTree(root.right);
root.right = invertTree(temp);
return root;
}
}
实现总结
- 针对递归:invertTree 方法通过递归调用实现了二叉树的翻转
- 针对二叉树:通过访问并交换节点的左右子树实现了翻转操作
- 边界条件处理:首先检查根节点是否为空,如果为空则直接返回 null
- 时间复杂度:O(n),其中 n 是二叉树中的节点数。这是因为在翻转每个节点时,都会对其左右子树进行递归调用,而每个节点只会被访问一次。对于每个节点,翻转操作的时间复杂度是常数级,即 O(1),因为只是交换左右子树的引用。递归调用的总次数是二叉树中节点的数量 n,因此总的时间复杂度为 O(n)
- 空间复杂度:O(h),其中 h 是二叉树的高度。递归调用过程中,系统需要维护一个递归调用栈,其空间占用取决于递归的深度。在最坏的情况下,当二叉树为一条链(即退化为链表)时,递归的深度为 h = n,其中 n 是节点数量。此时,递归调用栈的空间复杂度为 O(n)。在平衡二叉树的情况下,h 的值通常约为 log(n),因此空间复杂度为 O(log(n))。在代码中,递归调用栈的深度取决于二叉树的高度,因此空间复杂度主要受到二叉树的形状影响。