- 🎥 个人主页:Dikz12
- 🔥个人专栏:MySql
- 📕格言:那些在暗处执拗生长的花,终有一日会馥郁传香
- 欢迎大家👍点赞✍评论⭐收藏
目录
新增(Create)
全列插入
指定列插入
插入多行数据
查询 (Retrieve)
全列查询
指定列查询
查询字段为表达式
别名
去重
排序
条件查询 WHERE
分页查询LIMIT
修改(Update)
删除(Delete)
新增(Create)
全列插入
insert into 表名 values(值,值...);into 是可以省略的,不建议;此时的值是要和列相对应的(列的个数和类型)

指定列插入
insert into 表名 (列名,列名...) values (值,值...);
此处,只插入了name而id那一列就会填充为默认值
插入多行数据
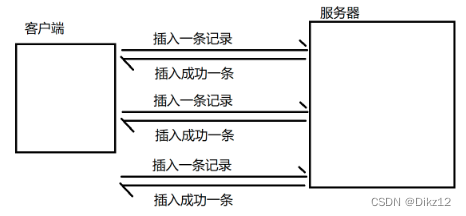
insert into 表名 values(值,值...),(值,值...);一次插入多行数据,相较于一次插入一行,分多次插入,要快不少。
涉及了三次网络交互!
这个是请求体积比之前大了。
查询 (Retrieve)
全列查询
select * from 表名;* 表示通配符,代指所有列。
mysql是一个“客户端-服务器”结构的程序!
客户端进行操作,都会通过请求发送给服务器,服务器查询的结果也就会通过响应返回给客户端。
如果表中的数据特别多,就会产生问题!
1.读取硬盘,把硬盘的IO跑满了。程序想访问其它硬盘就会很慢。
2.操作网络,也可能把网卡的带宽跑满。其他客户端想访问服务器,也会很慢。
指定列查询
select 列名,列名... from 表名; 
查询字段为表达式
一边查询,一边进行计算;在查询的是时候,写由列名构成的表达式,把这一列中的所有行带入表达式,参与运算。

这个操作不会修改数据库上的原始数据;进行查询的时候,是把服务器这里的数据读出来,返回给客户端,以临时表的形式进行展示。
别名
查询的时候给列/ 表达式 指定别名(给表也能指定别名) 不建议省略as.
select 列/表达式 as 别名 from 表名;
去重
distinct 关键词 修饰某个列 / 多个列,值相同的行,只保留一行


排序
select 列名 from 表名 order by 列名 asc/desc;asc 升序,desc 降序;如果省略,就是升序排序。

指定多个列来进行排序。order by 后面可以写多个列.使用 , 来分割
条件查询 WHERE
会根据具体的条件,按照条件对数据进行筛选. 满足条件,就会被放到结果集合中;不成立,就pass。
select 列名 from where 条件;
比较运算符:
| 运算符 | 说明 |
| >, >=, <, <= | 大于,大于等于,小于,小于等于 |
| = | 等于,NULL 不安全,例如 NULL = NULL 的结果是 NULL |
| <=> | 等于,NULL 安全,例如 NULL <=> NULL 的结果是 TRUE(1) |
| != | 不等于 |
| BETWEEN a0 AND a1 | 范围匹配,[a0, a1],如果 a0 <= value <= a1,返回 TRUE(1) |
| IN (option, ...) | 如果是 option 中的任意一个,返回 TRUE(1) |
| IS NULL | 是 NULL |
| IS NOT NULL | 不是 NULL |
| LIKE | 模糊匹配。% 表示任意多个(包括 0 个)任意字符;_ 表示任意一个字 符 |
逻辑运算符:
| 运算符 | 说明 |
| AND | 多个条件必须都为 TRUE(1),结果才是 TRUE(1) |
| OR | 任意一个条件为 TRUE(1), 结果为 TRUE(1) |
| NOT | 条件为 TRUE(1),结果为 FALSE(0) |
1. WHERE条件可以使用表达式,但不能使用别名。
2. AND的优先级高于OR,在同时使用时,需要使用小括号()包裹优先执行的部分就要理解,select的执行顺序:
1.遍历表中的记录
2.把记录的值,带入条件,进行筛选 (where 是第二步执行)
3.保留条件成立的记录。进行列上的表达式计算 (别名是在第三步)
4.如果有order by,所有行都记录之后,在针对结果进行排序
分页查询LIMIT
使用select * from 这种方式查询,是比较危险的;需要保证一次查询,不要查出来的东西太多。
limit可限制查询最多查出来多少个结果。
where 和 order by 可以省略.
select 列名 from 表名 [where] [order by] limit n;
select 列名 from 表名 [where] [order by] limit n offset s;
offset 偏移量,也就是一个“下标”;此处,就是移动了四次
修改(Update)
update 表名 set 列名=值 where 条件; where 条件 限制这次操作具体要修改那些行的数据。

不加任何条件,就是对所有行进行修改

decimal(3,1)表示长度为3,小数点1位;所以49.25就发生了数据截断。
删除(Delete)
delete from 表名 where 条件 /order by / limit ; 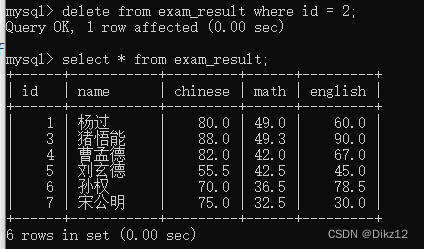
如果不指定任何操作,就是删除整个表;
delete和drop 还是有区别的,drop table 删除了表和表里的数据;delete 只删除表中的数据,表还在。
修改和删除是持久生效的,都会影响到数据库服务器硬盘中的数据!