数据结构

数据结构与算法

数据结构（英语：data structure）是计算机中存储、组织数据的方式。

数据结构是一种具有一定逻辑关系，在计算机中应用某种存储结构，并且封装了相应操作的数据元素集合。它包含三方面的内容，逻辑关系、存储关系及操作。

不同种类的数据结构适合于不同种类的应用，而部分甚至专门用于特定的作业任务。例如，计算机网络依赖于路由表运作，B 树高度适用于数据库的封装。

为什么要学习数据结构和算法？

随着应用程序变得越来越复杂和数据越来越丰富，几百万、几十亿甚至几百亿的数据就会出现，而对这么大对数据进行搜索、插入或者排序等的操作就越来越慢，数据结构就是用来解决这些问题的。

阅读本教程前，您需要了解的知识？

在您开始阅读本教程之前，您必须具备基本的 Java 编程的概念。如果您还不了解这些概念，那么建议您先阅读我们的 Java 教程。

常见的数据结构

• 栈（Stack）：栈是一种特殊的线性表，它只能在一个表的一个固定端进行数据结点的插入和删除操作。
• 队列（Queue）：队列和栈类似，也是一种特殊的线性表。和栈不同的是，队列只允许在表的一端进行插入操作，而在另一端进行删除操作。
• 数组（Array）：数组是一种聚合数据类型，它是将具有相同类型的若干变量有序地组织在一起的集合。
• 链表（Linked List）：链表是一种数据元素按照链式存储结构进行存储的数据结构，这种存储结构具有在物理上存在非连续的特点。
• 树（Tree）：树是典型的非线性结构，它是包括，2 个结点的有穷集合 K。
• 图（Graph）：图是另一种非线性数据结构。在图结构中，数据结点一般称为顶点，而边是顶点的有序偶对。
• 堆（Heap）：堆是一种特殊的树形数据结构，一般讨论的堆都是二叉堆。
• 散列表（Hash table）：散列表源自于散列函数(Hash function)，其思想是如果在结构中存在关键字和T相等的记录，那么必定在F(T)的存储位置可以找到该记录，这样就可以不用进行比较操作而直接取得所查记录。

常用算法

数据结构研究的内容：就是如何按一定的逻辑结构，把数据组织起来，并选择适当的存储表示方法把逻辑结构组织好的数据存储到计算机的存储器里。算法研究的目的是为了更有效的处理数据，提高数据运算效率。数据的运算是定义在数据的逻辑结构上，但运算的具体实现要在存储结构上进行。一般有以下几种常用运算：

• 检索：检索就是在数据结构里查找满足一定条件的节点。一般是给定一个某字段的值，找具有该字段值的节点。
• 插入：往数据结构中增加新的节点。
• 删除：把指定的结点从数据结构中去掉。
• 更新：改变指定节点的一个或多个字段的值。
• 排序：把节点按某种指定的顺序重新排列。例如递增或递减。

插入排序

一、概念及其介绍
插入排序(InsertionSort)，一般也被称为直接插入排序。

对于少量元素的排序，它是一个有效的算法。插入排序是一种最简单的排序方法，它的基本思想是将一个记录插入到已经排好序的有序表中，从而一个新的、记录数增 1 的有序表。在其实现过程使用双层循环，外层循环对除了第一个元素之外的所有元素，内层循环对当前元素前面有序表进行待插入位置查找，并进行移动。

二、适用说明
插入排序的平均时间复杂度也是 O(n^2)，空间复杂度为常数阶 O(1)，具体时间复杂度和数组的有序性也是有关联的。

插入排序中，当待排序数组是有序时，是最优的情况，只需当前数跟前一个数比较一下就可以了，这时一共需要比较 N-1 次，时间复杂度为 O(N)。最坏的情况是待排序数组是逆序的，此时需要比较次数最多，最坏的情况是 O(n^2)。

三、过程图示
假设前面 n-1(其中 n>=2)个数已经是排好顺序的，现将第 n 个数插到前面已经排好的序列中，然后找到合适自己的位置，使得插入第n个数的这个序列也是排好顺序的。

按照此法对所有元素进行插入，直到整个序列排为有序的过程，称为插入排序。

从小到大的插入排序整个过程如图示：

第一轮：从第二位置的 6 开始比较，比前面 7 小，交换位置。

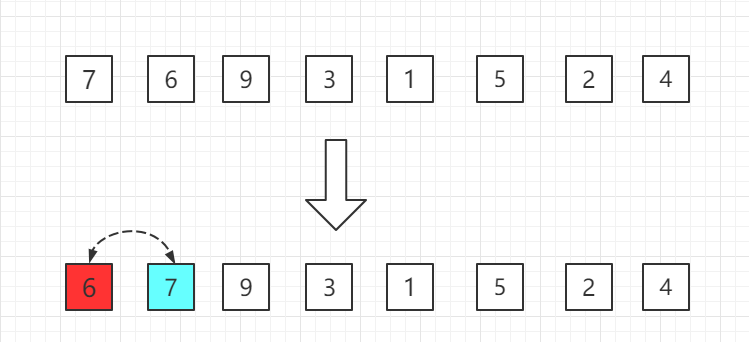
第二轮：第三位置的 9 比前一位置的 7 大，无需交换位置。

第三轮：第四位置的 3 比前一位置的 9 小交换位置，依次往前比较。

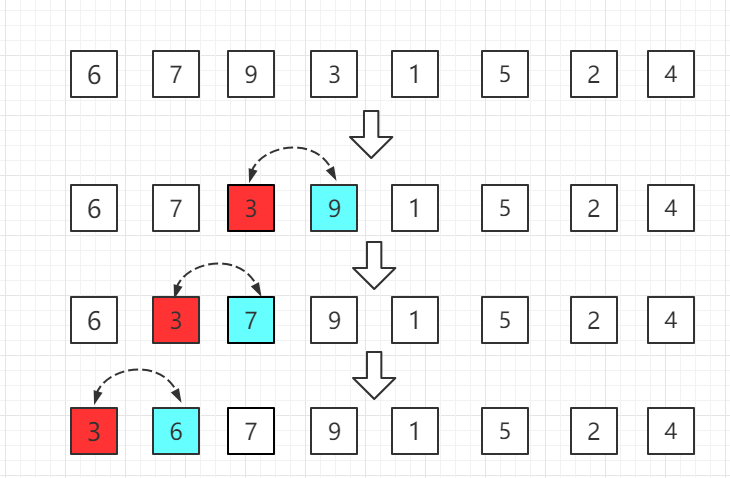
第四轮：第五位置的 1 比前一位置的 9 小，交换位置，再依次往前比较。

…

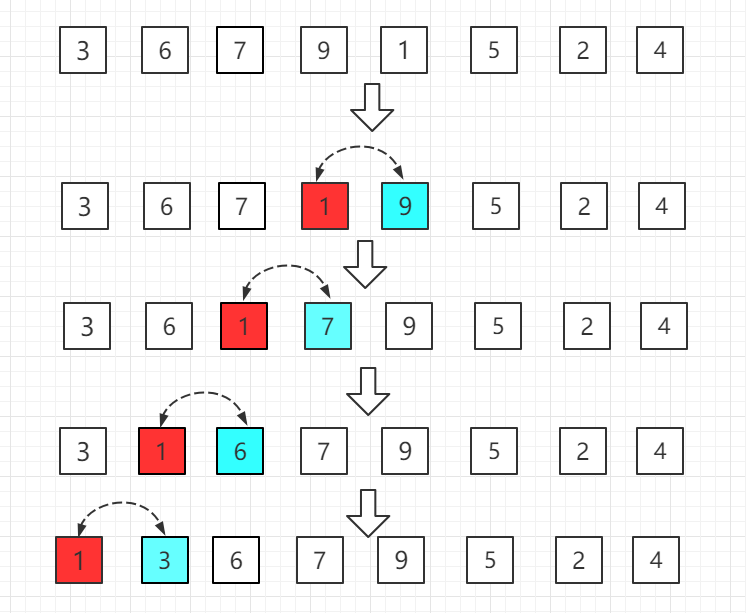
就这样依次比较到最后一个元素。

四、Java 实例代码

部分代码：

InsertionSort.java 文件代码：
package demo;

/**
 * 插入排序
 */
public class InsertionSort {
    //核心代码---开始
    public static void sort(Comparable[] arr){

        int n = arr.length;
        for (int i = 0; i < n; i++) {
            // 寻找元素 arr[i] 合适的插入位置
           for( int j = i ; j > 0 ; j -- )
                if( arr[j].compareTo( arr[j-1] ) < 0 )
                    swap( arr, j , j-1 );
                else
                    break;
        }
    }
    //核心代码---结束
    private static void swap(Object[] arr, int i, int j) {
        Object t = arr[i];
        arr[i] = arr[j];
        arr[j] = t;
    }

    public static void main(String[] args) {

        int N = 20000;
        Integer[] arr = SortTestHelper.generateRandomArray(N, 0, 100000);
        InsertionSort.sort(arr);
        for( int i = 0 ; i < arr.length ; i ++ ){
            System.out.print(arr[i]);
            System.out.print(' ');
        }
    }

}

希尔排序

一、概念及其介绍
希尔排序(Shell Sort)是插入排序的一种，它是针对直接插入排序算法的改进。

希尔排序又称缩小增量排序，因 DL.Shell 于 1959 年提出而得名。

它通过比较相距一定间隔的元素来进行，各趟比较所用的距离随着算法的进行而减小，直到只比较相邻元素的最后一趟排序为止。

二、适用说明
希尔排序时间复杂度是 O(n^(1.3-2))，空间复杂度为常数阶 O(1)。希尔排序没有时间复杂度为 O(n(logn)) 的快速排序算法快 ，因此对中等大小规模表现良好，但对规模非常大的数据排序不是最优选择，总之比一般 O(n^2 ) 复杂度的算法快得多。

三、过程图示
希尔排序目的为了加快速度改进了插入排序，交换不相邻的元素对数组的局部进行排序，并最终用插入排序将局部有序的数组排序。

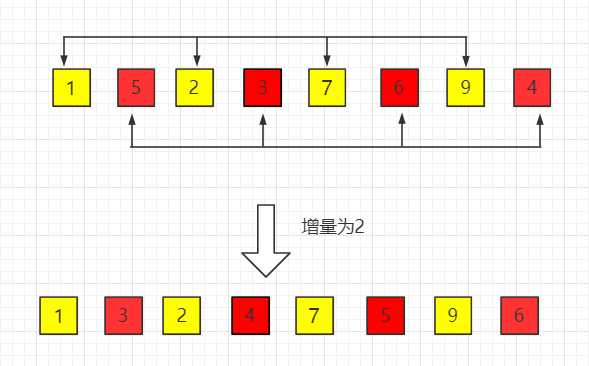
在此我们选择增量 gap=length/2，缩小增量以 gap = gap/2 的方式，用序列 {n/2,(n/2)/2…1} 来表示。

如图示例：

（1）初始增量第一趟 gap = length/2 = 4

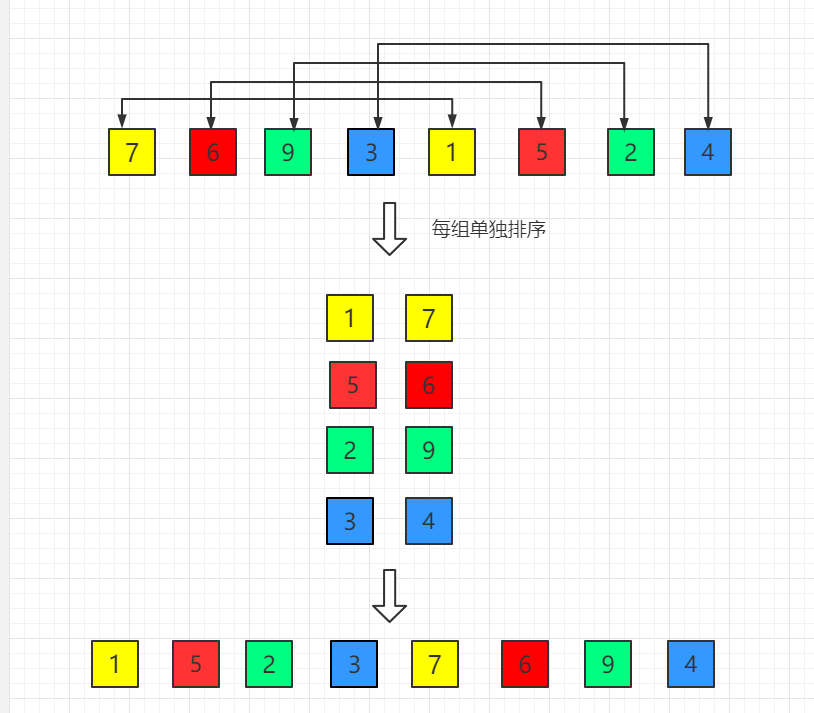
（2）第二趟，增量缩小为 2

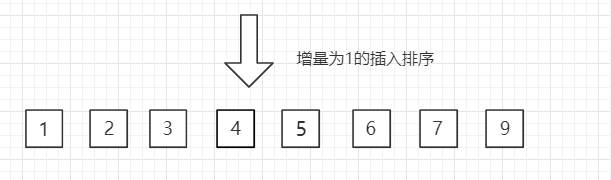
（3）第三趟，增量缩小为 1,得到最终排序结果

四、Java 实例代码
最内层循环其实就是插入排序:

ShellSort.java 文件代码： public class ShellSort {
    //核心代码---开始
    public static void sort(Comparable[] arr) {
        int j;
        for (int gap = arr.length / 2; gap >  0; gap /= 2) {
            for (int i = gap; i < arr.length; i++) {
                Comparable tmp = arr[i];
                for (j = i; j >= gap && tmp.compareTo(arr[j - gap]) < 0; j -= gap) {
                    arr[j] = arr[j - gap];
                }
                arr[j] = tmp;
            }
        }
    }
    //核心代码---结束
    public static void main(String[] args) {

        int N = 2000;
        Integer[] arr = SortTestHelper.generateRandomArray(N, 0, 10);
        ShellSort.sort(arr);
        for( int i = 0 ; i < arr.length ; i ++ ){
            System.out.print(arr[i]);
            System.out.print(' ');
        }
    } }

归并排序

一、概念及其介绍
归并排序（Merge sort）是建立在归并操作上的一种有效、稳定的排序算法，该算法是采用分治法(Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。

二、适用说明
当有 n 个记录时，需进行 logn 轮归并排序，每一轮归并，其比较次数不超过 n，元素移动次数都是 n，因此，归并排序的时间复杂度为 O(nlogn)。归并排序时需要和待排序记录个数相等的存储空间，所以空间复杂度为 O(n)。

归并排序适用于数据量大，并且对稳定性有要求的场景。

三、过程图示
归并排序是递归算法的一个实例，这个算法中基本的操作是合并两个已排序的数组，取两个输入数组 A 和 B，一个输出数组 C，以及三个计数器 i、j、k，它们初始位置置于对应数组的开始端。

A[i] 和 B[j] 中较小者拷贝到 C 中的下一个位置，相关计数器向前推进一步。

当两个输入数组有一个用完时候，则将另外一个数组中剩余部分拷贝到 C 中。

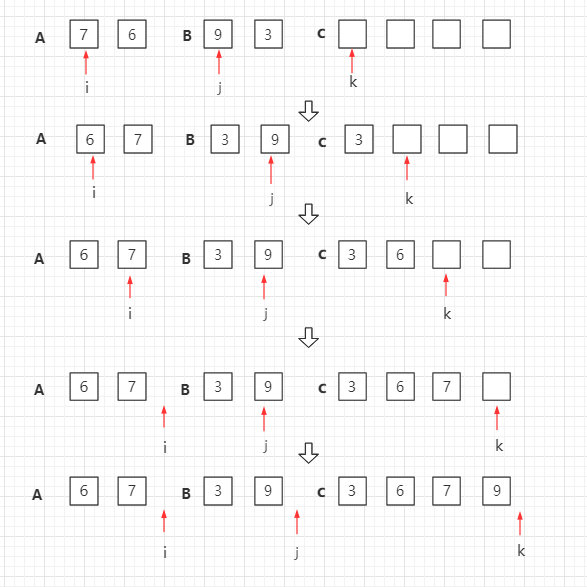
自顶向下的归并排序，递归分组图示：

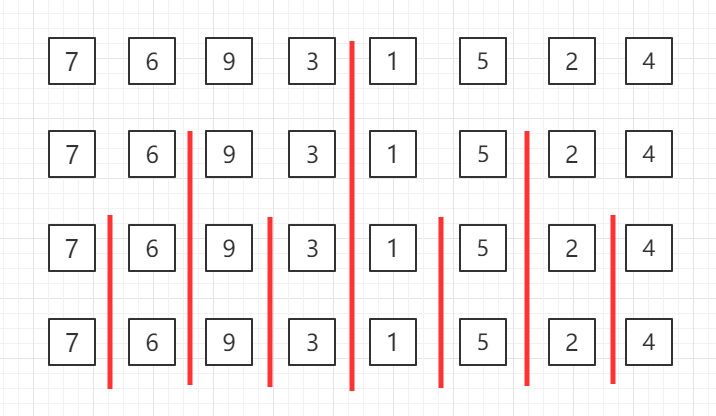
对第三行两个一组的数据进行归并排序

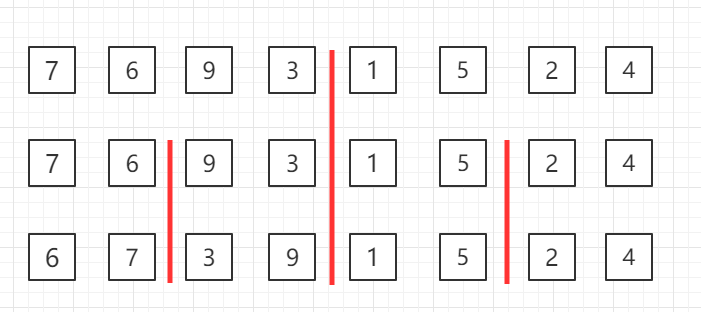
对第二行四个一组的数据进行归并排序

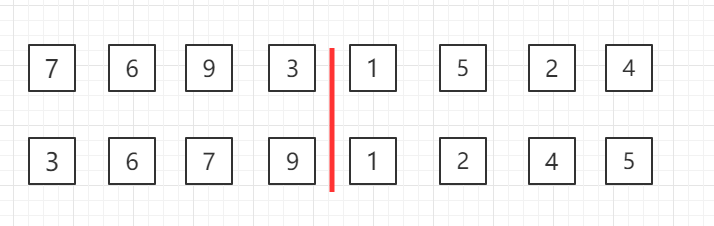
整体进行归并排序

四、Java 实例代码

MergeSort.java 文件代码：
public class MergeSort {

    // 将arr[l...mid]和arr[mid+1...r]两部分进行归并
    private static void merge(Comparable[] arr, int l, int mid, int r) {

        Comparable[] aux = Arrays.copyOfRange(arr, l, r + 1);

        // 初始化，i指向左半部分的起始索引位置l；j指向右半部分起始索引位置mid+1
        int i = l, j = mid + 1;
        for (int k = l; k <= r; k++) {

            if (i > mid) {  // 如果左半部分元素已经全部处理完毕
                arr[k] = aux[j - l];
                j++;
            } else if (j > r) {   // 如果右半部分元素已经全部处理完毕
                arr[k] = aux[i - l];
                i++;
            } else if (aux[i - l].compareTo(aux[j - l]) < 0) {  // 左半部分所指元素 < 右半部分所指元素
                arr[k] = aux[i - l];
                i++;
            } else {  // 左半部分所指元素 >= 右半部分所指元素
                arr[k] = aux[j - l];
                j++;
            }
        }
    }

    // 递归使用归并排序,对arr[l...r]的范围进行排序
    private static void sort(Comparable[] arr, int l, int r) {
        if (l >= r) {
            return;
        }
        int mid = (l + r) / 2;
        sort(arr, l, mid);
        sort(arr, mid + 1, r);
        // 对于arr[mid] <= arr[mid+1]的情况,不进行merge
        // 对于近乎有序的数组非常有效,但是对于一般情况,有一定的性能损失
        if (arr[mid].compareTo(arr[mid + 1]) > 0)
            merge(arr, l, mid, r);
    }

    public static void sort(Comparable[] arr) {

        int n = arr.length;
        sort(arr, 0, n - 1);
    }

    // 测试MergeSort
    public static void main(String[] args) {

        int N = 1000;
        Integer[] arr = SortTestHelper.generateRandomArray(N, 0, 100000);
        sort(arr);
        //打印数组
        SortTestHelper.printArray(arr);
    }
}

随机机化快速排序

一、概念及其介绍
快速排序由 C. A. R. Hoare 在 1960 年提出。

随机化快速排序基本思想：通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

二、适用说明
快速排序是一种比较快速的排序算法，它的平均运行时间是 O(nlogn)，之所以特别快是由于非常精练和高度优化的内部循环，最坏的情形性能为 O(n^2)。像归并一样，快速排序也是一种分治的递归算法。从空间性能上看，快速排序只需要一个元素的辅助空间，但快速排序需要一个栈空间来实现递归，空间复杂度也为O(logn)。

三、过程图示
在一个数组中选择一个基点，比如第一个位置的 4，然后把4挪到正确位置，使得之前的子数组中数据小于 4，之后的子数组中数据大于 4，然后逐渐递归下去完成整个排序。

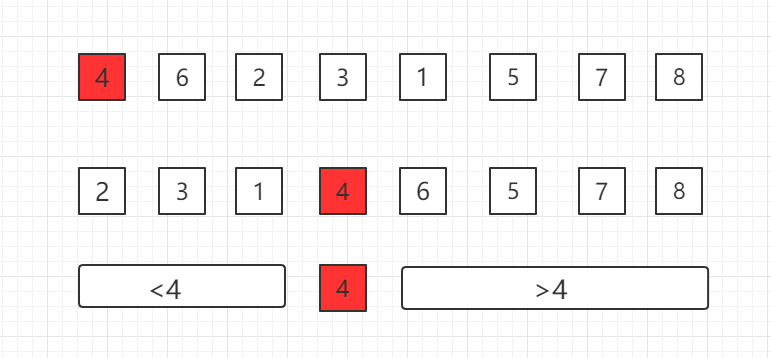
如何和把选定的基点数据挪到正确位置上，这是快速排序的核心，我们称为 Partition。

过程如下所示，其中 i 为当前遍历比较的元素位置：

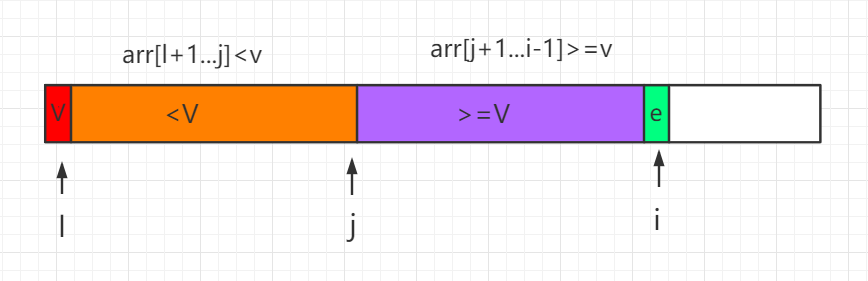
这个 partition 过程用代码表示为：

实例
…

private static int partition(Comparable[] arr, int l, int r){
    Comparable v = arr[l];

    int j = l;
    for( int i = l + 1 ; i <= r ; i ++ )
        if( arr[i].compareTo(v) < 0 ){
            j ++;
            //数组元素位置交换
            swap(arr, j, i);
        }

    swap(arr, l, j);

    return j;
}

…
如果是对近乎有序的数组进行快速排序，每次 partition 分区后子数组大小极不平衡，容易退化成 O(n^2) 的时间复杂度算法。我们需要对上述代码进行优化，随机选择一个基点做为比较，称为随机化快速排序算法。只需要在上述代码前加上下面一行，随机选择数组中一数据和基点数据进行交换。

swap( arr, l , (int)(Math.random()*(r-l+1))+l );

四、Java 实例代码

QuickSort.java 文件代码：
package xxx;

/**
 * 随机化快速排序
 */
public class QuickSort {


    // 对arr[l...r]部分进行partition操作
    // 返回p, 使得arr[l...p-1] < arr[p] ; arr[p+1...r] > arr[p]
    private static int partition(Comparable[] arr, int l, int r){

        // 随机在arr[l...r]的范围中, 选择一个数值作为标定点pivot
        swap( arr, l , (int)(Math.random()*(r-l+1))+l );
        Comparable v = arr[l];
        // arr[l+1...j] < v ; arr[j+1...i) > v
        int j = l;
        for( int i = l + 1 ; i <= r ; i ++ )
            if( arr[i].compareTo(v) < 0 ){
                j ++;
                swap(arr, j, i);
            }
        swap(arr, l, j);
        return j;
    }

    // 递归使用快速排序,对arr[l...r]的范围进行排序
    private static void sort(Comparable[] arr, int l, int r){
        if (l >= r) {
            return;
        }
        int p = partition(arr, l, r);
        sort(arr, l, p-1 );
        sort(arr, p+1, r);
    }

    public static void sort(Comparable[] arr){
        int n = arr.length;
        sort(arr, 0, n-1);
    }

    private static void swap(Object[] arr, int i, int j) {
        Object t = arr[i];
        arr[i] = arr[j];
        arr[j] = t;
    }

    // 测试 QuickSort
    public static void main(String[] args) {

        // Quick Sort也是一个O(nlogn)复杂度的算法
        // 可以在1秒之内轻松处理100万数量级的数据
        int N = 1000000;
        Integer[] arr = SortTestHelper.generateRandomArray(N, 0, 100000);
        sort(arr);
        SortTestHelper.printArray(arr);

    }
}

双路快速排序

一、概念及其介绍
双路快速排序算法是随机化快速排序的改进版本，partition 过程使用两个索引值（i、j）用来遍历数组，将 <v 的元素放在索引i所指向位置的左边，而将 >v 的元素放在索引j所指向位置的右边，v 代表标定值。

二、适用说明
时间和空间复杂度同随机化快速排序。 对于有大量重复元素的数组，如果使用上一节随机化快速排序效率是非常低的，导致 partition 后大于基点或者小于基点数据的子数组长度会极度不平衡，甚至会退化成 O(n*2) 时间复杂度的算法，对这种情况可以使用双路快速排序算法。

三、过程图示
使用两个索引值（i、j）用来遍历我们的序列，将 <=v 的元素放在索引 i 所指向位置的左边，而将 >=v 的元素放在索引 j 所指向位置的右边，平衡左右两边子数组。

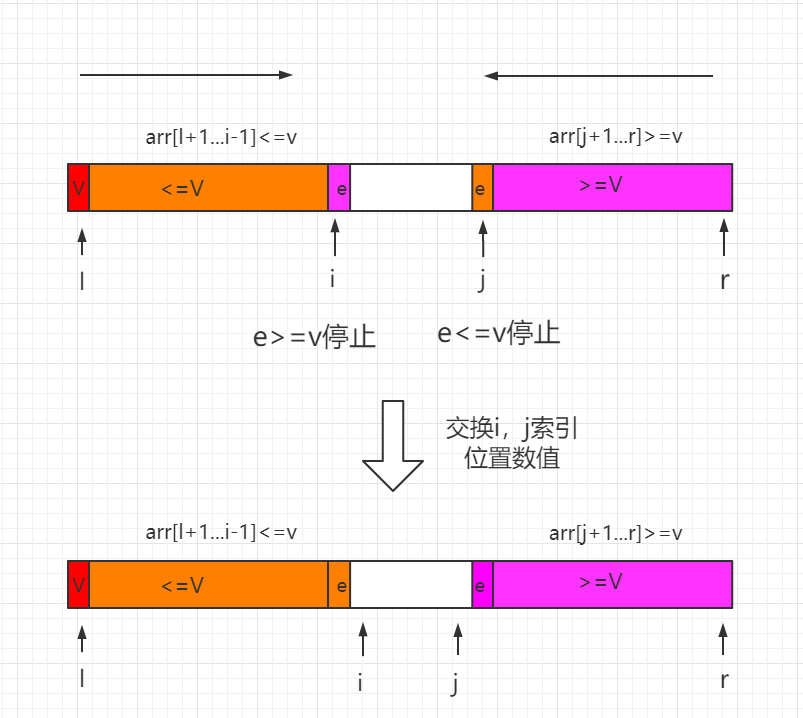
四、Java 实例代码

QuickSort2Ways.java 文件代码：

package demo;

/**
 * 双路快速排序
 */
public class QuickSort2Ways {

    //核心代码---开始
    private static int partition(Comparable[] arr, int l, int r){
        // 随机在arr[l...r]的范围中, 选择一个数值作为标定点pivot
        swap( arr, l , (int)(Math.random()*(r-l+1))+l );
        Comparable v = arr[l];
        // arr[l+1...i) <= v; arr(j...r] >= v
        int i = l+1, j = r;
        while( true ){
            while( i <= r && arr[i].compareTo(v) < 0 )
                i ++;
            while( j >= l+1 && arr[j].compareTo(v) > 0 )
                j --;
            if( i > j )
                break;
            swap( arr, i, j );
            i ++;
            j --;
        }
        swap(arr, l, j);
        return j;
    }
    //核心代码---结束

    // 递归使用快速排序,对arr[l...r]的范围进行排序
    private static void sort(Comparable[] arr, int l, int r){
        if (l >= r) {
            return;
        }
        int p = partition(arr, l, r);
        sort(arr, l, p-1 );
        sort(arr, p+1, r);
    }

    public static void sort(Comparable[] arr){

        int n = arr.length;
        sort(arr, 0, n-1);
    }

    private static void swap(Object[] arr, int i, int j) {
        Object t = arr[i];
        arr[i] = arr[j];
        arr[j] = t;
    }

    // 测试 QuickSort
    public static void main(String[] args) {

        // 双路快速排序算法也是一个O(nlogn)复杂度的算法
        // 可以在1秒之内轻松处理100万数量级的数据

        // Quick Sort也是一个O(nlogn)复杂度的算法
        // 可以在1秒之内轻松处理100万数量级的数据
        int N = 1000000;
        Integer[] arr = SortTestHelper.generateRandomArray(N, 0, 100000);
        sort(arr);
        SortTestHelper.printArray(arr);

    }
}

三路排序算法

一、概念及其介绍
三路快速排序是双路快速排序的进一步改进版本，三路排序算法把排序的数据分为三部分，分别为小于 v，等于 v，大于 v，v 为标定值，这样三部分的数据中，等于 v 的数据在下次递归中不再需要排序，小于 v 和大于 v 的数据也不会出现某一个特别多的情况），通过此方式三路快速排序算法的性能更优。

二、适用说明
时间和空间复杂度同随机化快速排序。

三路快速排序算法是使用三路划分策略对数组进行划分，对处理大量重复元素的数组非常有效提高快速排序的过程。它添加处理等于划分元素值的逻辑，将所有等于划分元素的值集中在一起。

三、过程图示

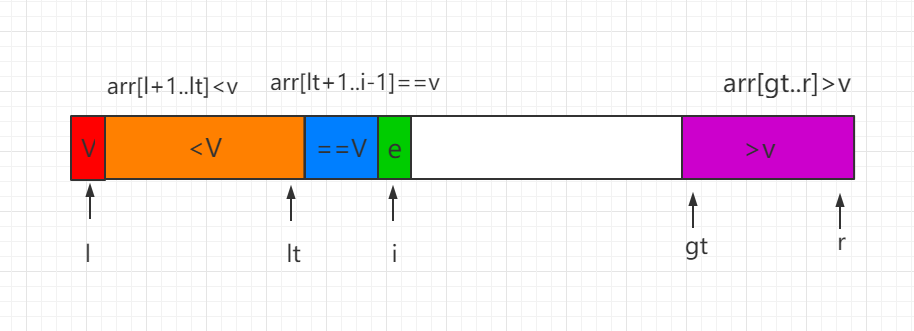
我们分三种情况进行讨论 partiton 过程，i 表示遍历的当前索引位置：

（1）当前处理的元素 e=V，元素 e 直接纳入蓝色区间，同时i向后移一位。

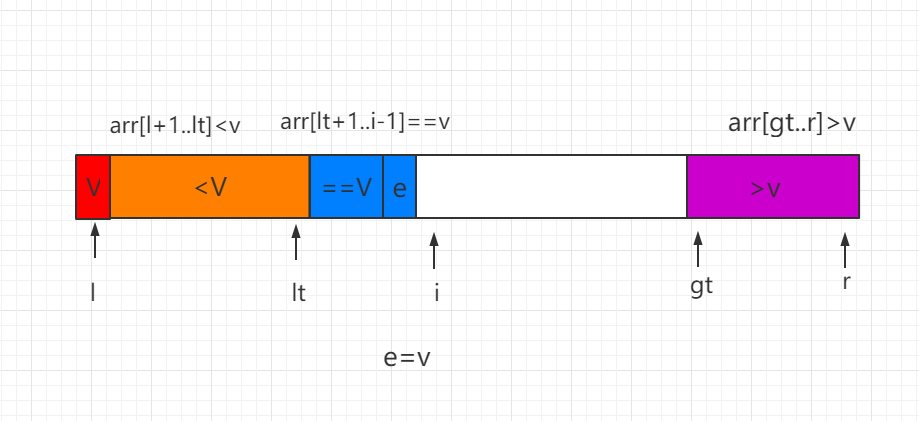
（2）当前处理元素 e<v，e 和等于 V 区间的第一个位置数值进行交换，同时索引 lt 和 i 都向后移动一位

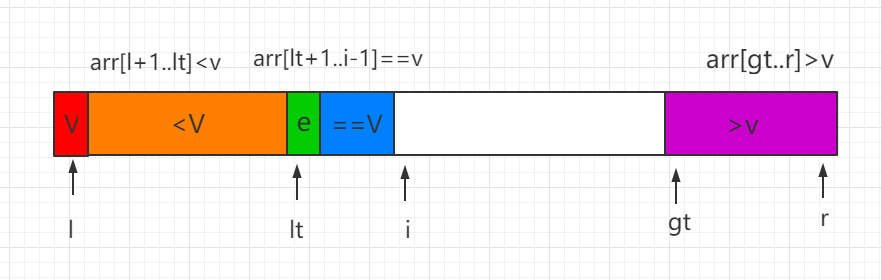
（3）当前处理元素 e>v，e 和 gt-1 索引位置的数值进行交换，同时 gt 索引向前移动一位。

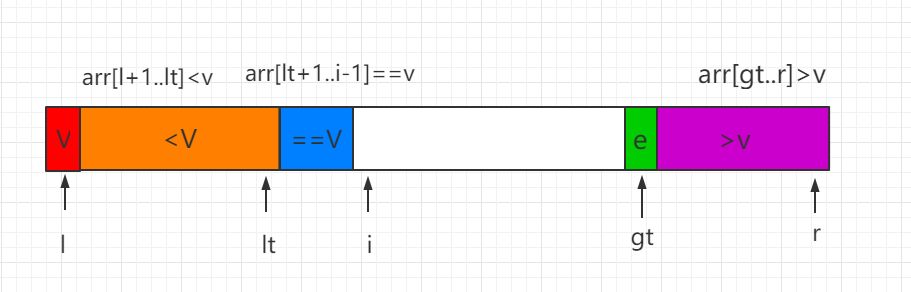
最后当 i=gt 时，结束遍历，同时需要把 v 和索引 lt 指向的数值进行交换，这样这个排序过程就完成了，然后对 <V 和 >V 的数组部分用同样的方法再进行递归排序。

四、Java 实例代码

QuickSort3Ways.java 文件代码：
package demo;

/**
 * 三路快速排序
 */
public class QuickSort3Ways {
    //核心代码---开始
    // 递归使用快速排序,对arr[l...r]的范围进行排序
    private static void sort(Comparable[] arr, int l, int r){
        if (l >= r) {
            return;
        }
        // 随机在arr[l...r]的范围中, 选择一个数值作为标定点pivot
        swap( arr, l, (int)(Math.random()*(r-l+1)) + l );
        Comparable v = arr[l];
        int lt = l;     // arr[l+1...lt] < v
        int gt = r + 1; // arr[gt...r] > v
        int i = l+1;    // arr[lt+1...i) == v
        while( i < gt ){
            if( arr[i].compareTo(v) < 0 ){
                swap( arr, i, lt+1);
                i ++;
                lt ++;
            }
            else if( arr[i].compareTo(v) > 0 ){
                swap( arr, i, gt-1);
                gt --;
            }
            else{ // arr[i] == v
                i ++;
            }
        }
        swap( arr, l, lt );
        sort(arr, l, lt-1);
        sort(arr, gt, r);
    }
    //核心代码---结束

    public static void sort(Comparable[] arr){

        int n = arr.length;
        sort(arr, 0, n-1);
    }

    private static void swap(Object[] arr, int i, int j) {
        Object t = arr[i];
        arr[i] = arr[j];
        arr[j] = t;
    }

    // 测试 QuickSort3Ways
    public static void main(String[] args) {

        // 三路快速排序算法也是一个O(nlogn)复杂度的算法
        // 可以在1秒之内轻松处理100万数量级的数据
        int N = 1000000;
        Integer[] arr = SortTestHelper.generateRandomArray(N, 0, 100000);
        sort(arr);
        SortTestHelper.printArray(arr);
    }
}

排序算法衍生问题

本小节对本教程的排序算法做一个总结。

（1）归并排序和快速排序都使用了分治算法。
顾名思义，就是将原问题分割查能同等结构的子问题，之后将子问题逐一解决后，原问题也就得到了解决。

（2）逆序对的定义
如果存在正整数 i, j 使得 1 ≤ i < j ≤ n 而且 A[i] > A[j]，则 <A[i], A[j]> 这个有序对称为 A 的一个逆序对。我们可以使用本教程的归并思想求逆序对的数量。

（3）取数组中第 n 大的元素
并不需要对整个数组进行排序，使用快速排序的思路求数组中第 n 大元素算法复杂度为 O(n)。

堆

堆的基本存储

一、概念及其介绍
堆(Heap)是计算机科学中一类特殊的数据结构的统称。

堆通常是一个可以被看做一棵完全二叉树的数组对象。

堆满足下列性质：

• 堆中某个节点的值总是不大于或不小于其父节点的值。
• 堆总是一棵完全二叉树。

二、适用说明
堆是利用完全二叉树的结构来维护一组数据，然后进行相关操作，一般的操作进行一次的时间复杂度在 O(1)~O(logn) 之间，堆通常用于动态分配和释放程序所使用的对象。

若为优先队列的使用场景，普通数组或者顺序数组，最差情况为 O(n^2)，堆这种数据结构也可以提高入队和出队的效率。

-	入队	出队
普通数组	O(1)	O(n)
顺序数组	O(n)	O(1)
堆	O(logn)	O(log)

三、结构图示
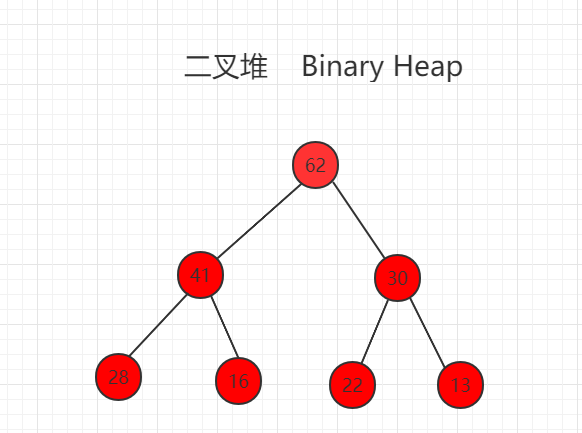
二叉堆是一颗完全二叉树，且堆中某个节点的值总是不大于其父节点的值，该完全二叉树的深度为 k，除第 k 层外，其它各层 (1～k-1) 的结点数都达到最大个数，第k 层所有的结点都连续集中在最左边。

其中堆的根节点最大称为最大堆，如下图所示：

我们可以使用数组存储二叉堆，右边的标号是数组的索引。

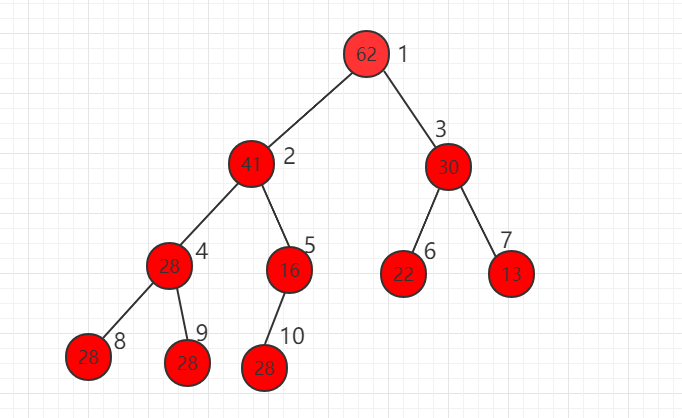
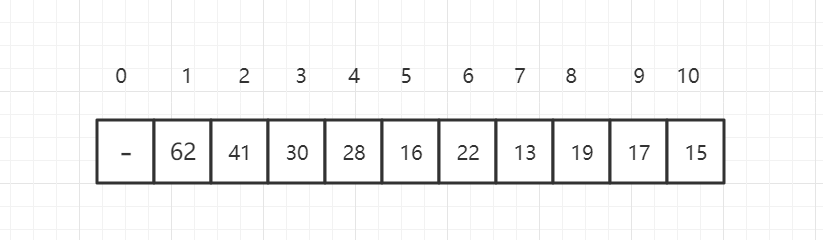
假设当前元素的索引位置为 i，可以得到规律：

parent(i) = i/2（取整）
left child(i) = 2*i
right child(i) = 2*i +1

四、Java 实例代码

src/demo/heap/MaxHeap.java 文件代码：
package demo.heap;

/**
 * 堆定义
 */
public class MaxHeap<T> {
    private T[] data;
    private int count;
    // 构造函数, 构造一个空堆, 可容纳capacity个元素
    public MaxHeap(int capacity){
        data = (T[])new Object[capacity+1];
        count = 0;
    }
    // 返回堆中的元素个数
    public int size(){
        return count;
    }
    // 返回一个布尔值, 表示堆中是否为空
    public boolean isEmpty(){
        return count == 0;
    }
    // 测试 MaxHeap
    public static void main(String[] args) {
        MaxHeap<Integer> maxHeap = new MaxHeap<Integer>(100);
        System.out.println(maxHeap.size());
    }
}

堆的 shift up

本小节介绍如何向一个最大堆中添加元素，称为 shift up。

假设我们对下面的最大堆新加入一个元素52，放在数组的最后一位，52大于父节点16，此时不满足堆的定义，需要进行调整。

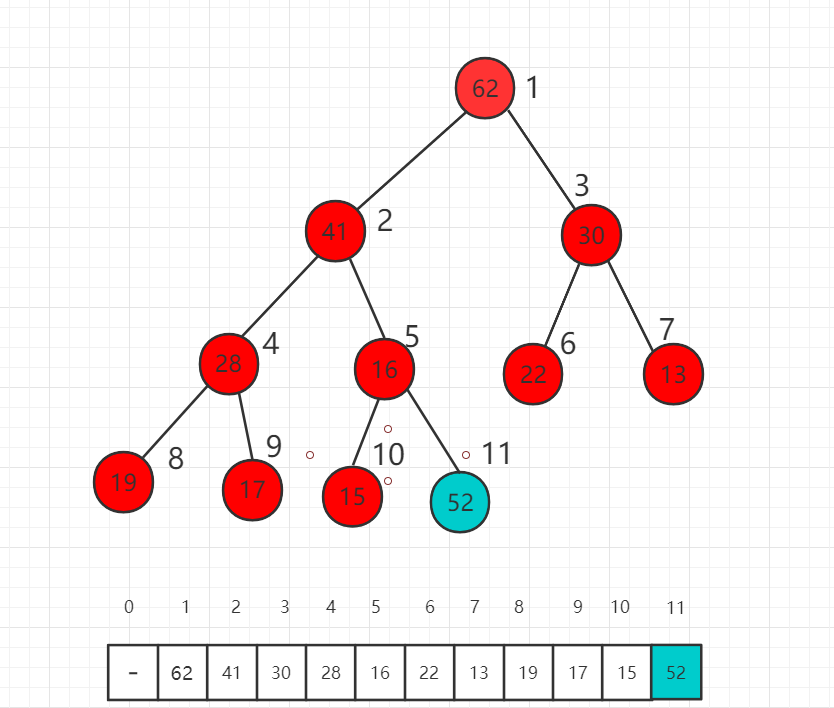
首先交换索引为 5 和 11 数组中数值的位置，也就是 52 和 16 交换位置。

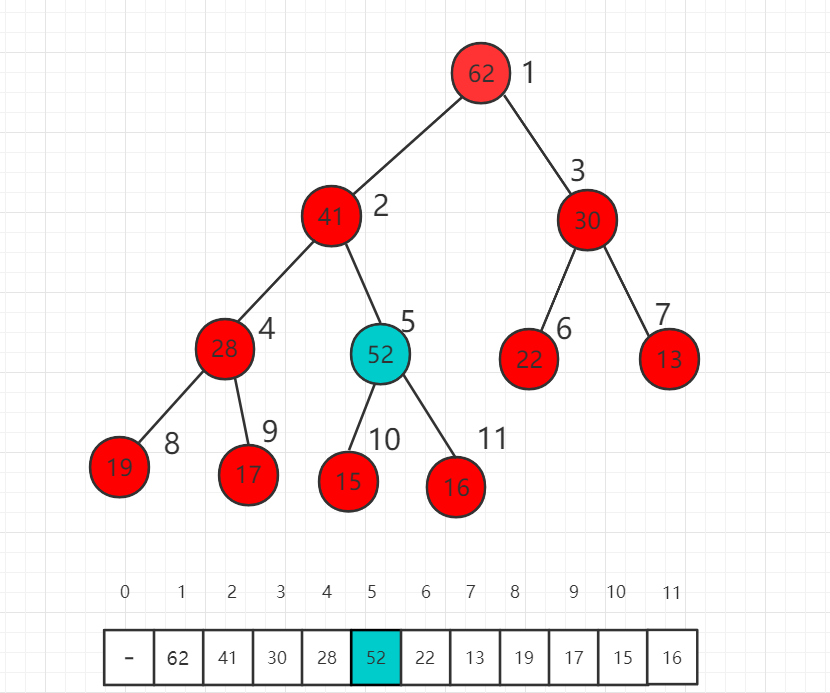
此时 52 依然比父节点索引为 2 的数值 41 大，我们还需要进一步挪位置。

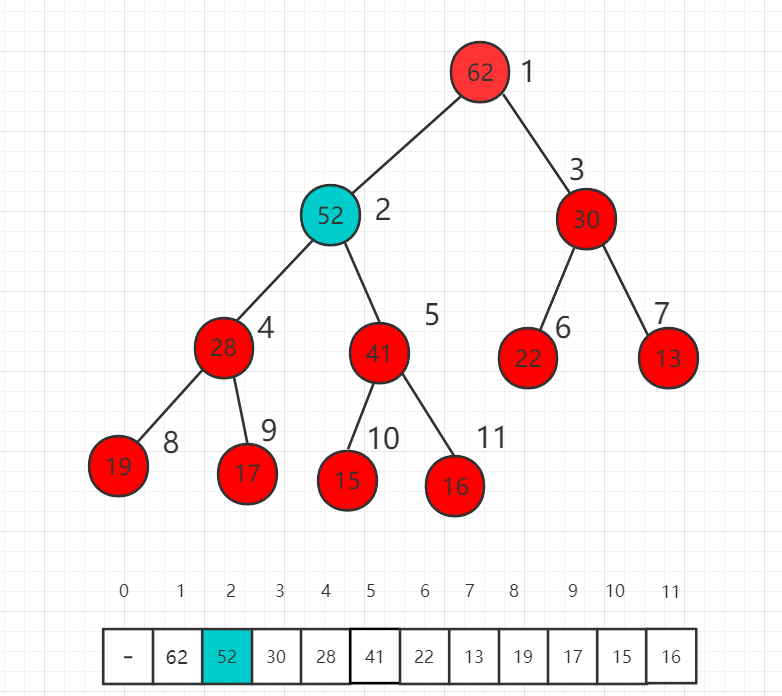
这时比较 52 和 62 的大小，52 已经比父节点小了，不需要再上升了，满足最大堆的定义。我们称这个过程为最大堆的 shift up。

Java 实例代码

src/demo/heap/HeapShiftUp.java 文件代码：
package demo.heap;

/**
 * 往堆中添加一元素
 */
public class HeapShiftUp<T extends Comparable> {

    protected T[] data;
    protected int count;
    protected int capacity;

    // 构造函数, 构造一个空堆, 可容纳capacity个元素
    public HeapShiftUp(int capacity){
        data = (T[])new Comparable[capacity+1];
        count = 0;
        this.capacity = capacity;
    }
    // 返回堆中的元素个数
    public int size(){
        return count;
    }

    // 返回一个布尔值, 表示堆中是否为空
    public boolean isEmpty(){
        return count == 0;
    }
    // 像最大堆中插入一个新的元素 item
    public void insert(T item){
        assert count + 1 <= capacity;
        data[count+1] = item;
        count ++;
        shiftUp(count);
    }
    // 交换堆中索引为i和j的两个元素
    private void swap(int i, int j){
        T t = data[i];
        data[i] = data[j];
        data[j] = t;
    }

    //********************
    //* 最大堆核心辅助函数
    //********************
    private void shiftUp(int k){

        while( k > 1 && data[k/2].compareTo(data[k]) < 0 ){
            swap(k, k/2);
            k /= 2;
        }
    }

    // 测试 HeapShiftUp
    public static void main(String[] args) {
        HeapShiftUp<Integer> heapShiftUp = new HeapShiftUp<Integer>(100);
        int N = 50; // 堆中元素个数
        int M = 100; // 堆中元素取值范围[0, M)
        for( int i = 0 ; i < N ; i ++ )
            heapShiftUp.insert( new Integer((int)(Math.random() * M)) );
        System.out.println(heapShiftUp.size());

    }
}

堆的 shift down

本小节将介绍如何从一个最大堆中取出一个元素，称为 shift down，只能取出最大优先级的元素，也就是根节点，把原来的 62 取出后，下面介绍如何填补这个最大堆。

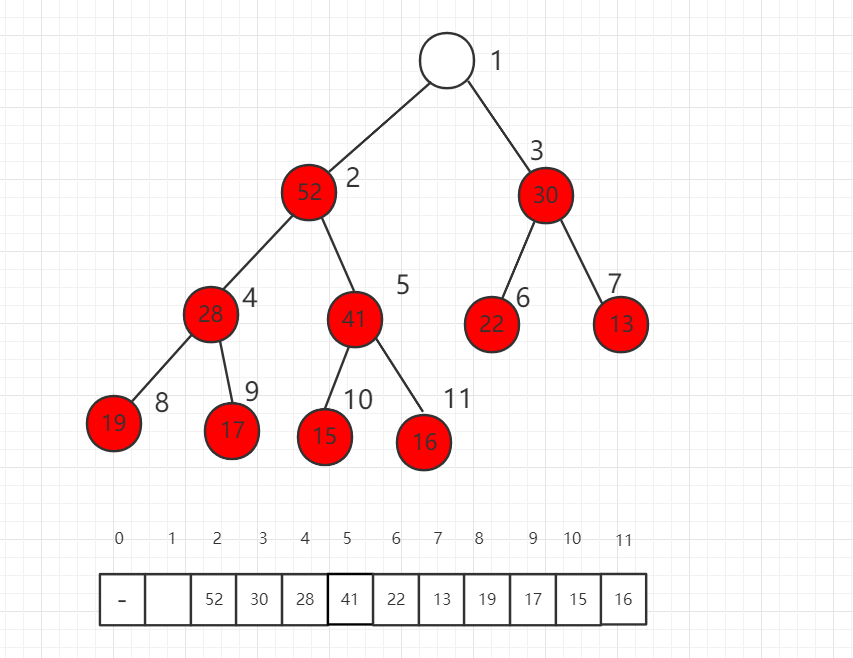
第一步，我们将数组最后一位数组放到根节点，此时不满足最大堆的定义。

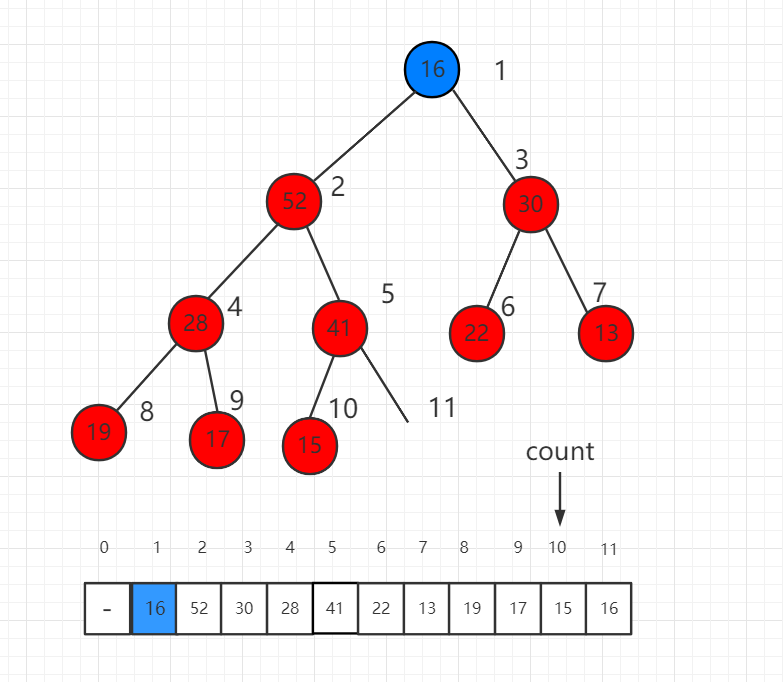
调整的过程是将这个根节点 16 一步一步向下挪，16 比子节点都小，先比较子节点 52 和 30 哪个大，和大的交换位置。

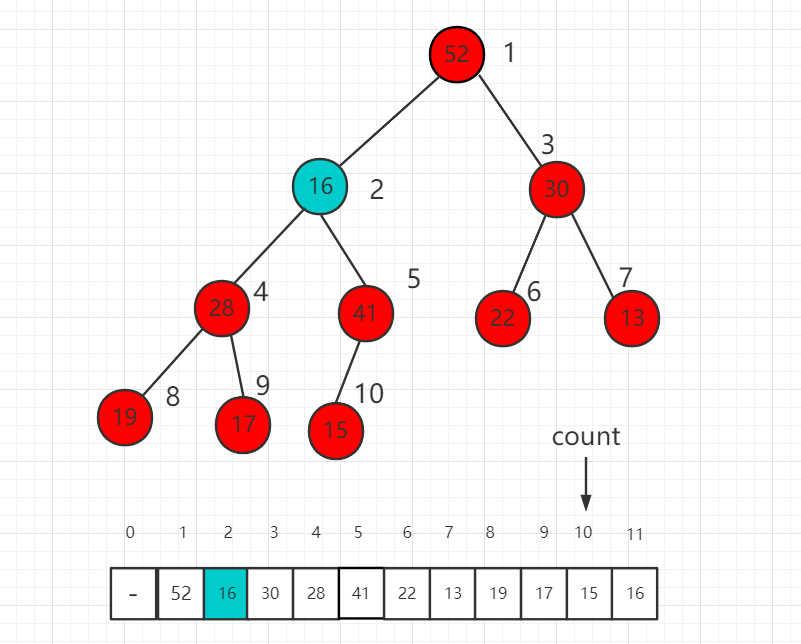
继续比较 16 的子节点 28 和 41，41 大，所以 16 和 41 交换位置。

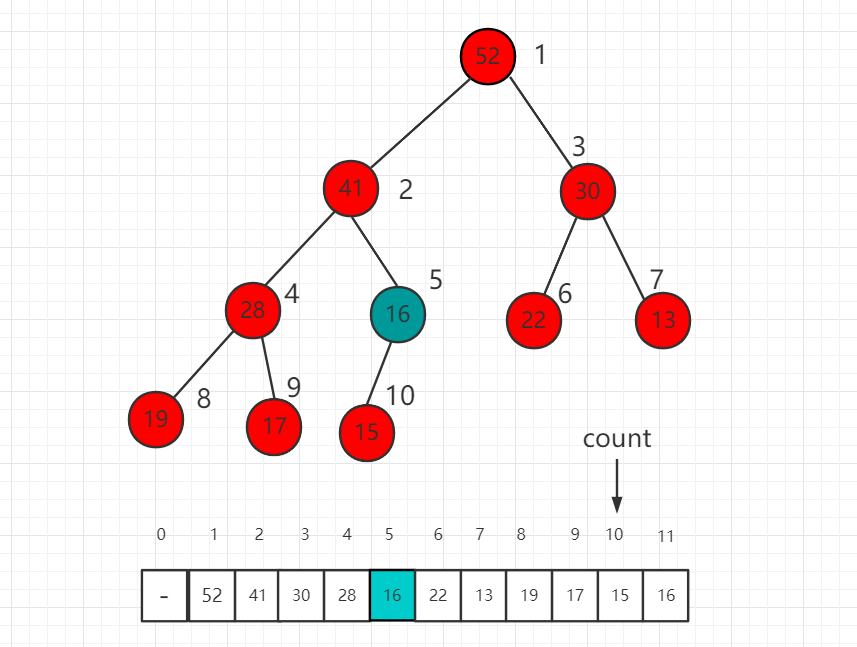
继续 16 和孩子节点 15 进行比较，16 大，所以现在不需要进行交换，最后我们的 shift down 操作完成，维持了一个最大堆的性质。

四、Java 实例代码

src/demo/heap/HeapShiftDown.java 文件代码：
package demo.heap;

/**
 * 往最大堆中取出一个元素
 */
public class HeapShiftDown<T extends Comparable> {

    protected T[] data;
    protected int count;
    protected int capacity;

    // 构造函数, 构造一个空堆, 可容纳capacity个元素
    public HeapShiftDown(int capacity){
        //这里加1是指原来能装的元素个数，那去掉0位，只能装capacity个元素
        data = (T[])new Comparable[capacity+1];
        count = 0;
        this.capacity = capacity;
    }
    // 返回堆中的元素个数
    public int size(){
        return count;
    }
    // 返回一个布尔值, 表示堆中是否为空
    public boolean isEmpty(){
        return count == 0;
    }
    // 像最大堆中插入一个新的元素 item
    public void insert(T item){

        assert count + 1 <= capacity;
        data[count+1] = item;
        count ++;
        shiftUp(count);
    }
    // 从最大堆中取出堆顶元素, 即堆中所存储的最大数据
    public T extractMax(){
        assert count > 0;
        T ret = data[1];
        swap( 1 , count );
        count --;
        shiftDown(1);
        return ret;
    }
    // 获取最大堆中的堆顶元素
    public T getMax(){
        assert( count > 0 );
        return data[1];
    }
    // 交换堆中索引为i和j的两个元素
    private void swap(int i, int j){
        T t = data[i];
        data[i] = data[j];
        data[j] = t;
    }

    //********************
    //* 最大堆核心辅助函数
    //********************
    private void shiftUp(int k){

        while( k > 1 && data[k/2].compareTo(data[k]) < 0 ){
            swap(k, k/2);
            k /= 2;
        }
    }
    //shiftDown操作
    private void shiftDown(int k){
        while( 2*k <= count ){
            int j = 2*k; // 在此轮循环中,data[k]和data[j]交换位置
            if( j+1 <= count && data[j+1].compareTo(data[j]) > 0 )
                j ++;
            // data[j] 是 data[2*k]和data[2*k+1]中的最大值
            if( data[k].compareTo(data[j]) >= 0 ) break;
            swap(k, j);
            k = j;
        }
        System.out.println("shiftDown结束");
    }

    // 测试 HeapShiftDown
    public static void main(String[] args) {
        HeapShiftDown<Integer> heapShiftDown = new HeapShiftDown<Integer>(100);
        // 堆中元素个数
        int N = 100;
        // 堆中元素取值范围[0, M)
        int M = 100;
        for( int i = 0 ; i < N ; i ++ )
            heapShiftDown.insert( new Integer((int)(Math.random() * M)) );
        Integer[] arr = new Integer[N];
        // 将最大堆中的数据逐渐使用extractMax取出来
        // 取出来的顺序应该是按照从大到小的顺序取出来的
        for( int i = 0 ; i < N ; i ++ ){
            arr[i] = heapShiftDown.extractMax();
            System.out.print(arr[i] + " ");
        }
        // 确保arr数组是从大到小排列的
        for( int i = 1 ; i < N ; i ++ )
            assert arr[i-1] >= arr[i];
    }
}

基础堆排序

一、概念及其介绍
堆排序（Heapsort）是指利用堆这种数据结构所设计的一种排序算法。

堆是一个近似 完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。

二、适用说明
我们之前构造堆的过程是一个个数据调用 insert 方法使用 shift up 逐个插入到堆中，这个算法的时候时间复杂度是 O(nlogn)，本小节介绍的一种构造堆排序的过程，称为 Heapify，算法时间复杂度为 O(n)。

三、过程图示
完全二叉树有个重要性质，对于第一个非叶子节点的索引是 n/2 取整数得到的索引值，其中 n 是元素个数(前提是数组索引从 1 开始计算)。

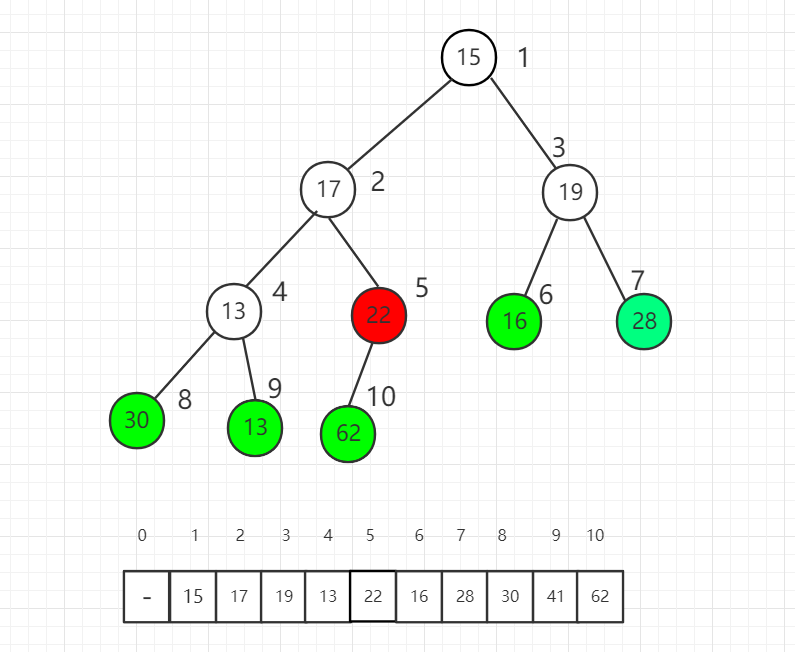
索引 5 位置是第一个非叶子节点，我们从它开始逐一向前分别把每个元素作为根节点进行 shift down 操作满足最大堆的性质。

索引 5 位置进行 shift down 操作后，22 和 62 交换位置。

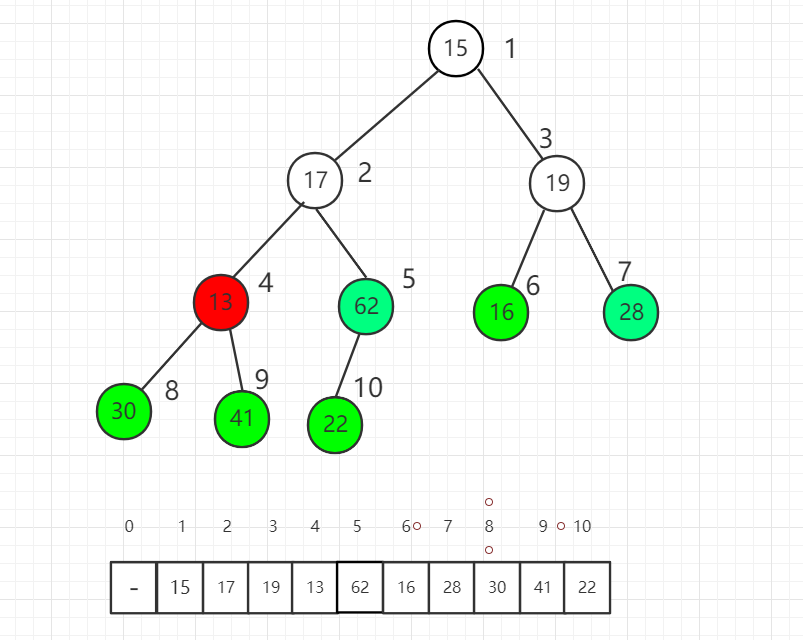
对索引 4 元素进行 shift down 操作

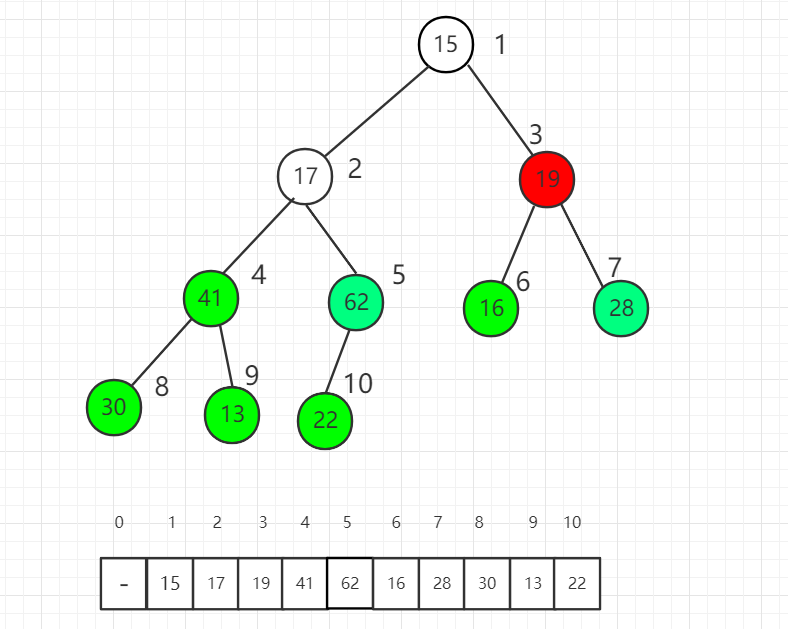
对索引 3 元素进行 shift down 操作

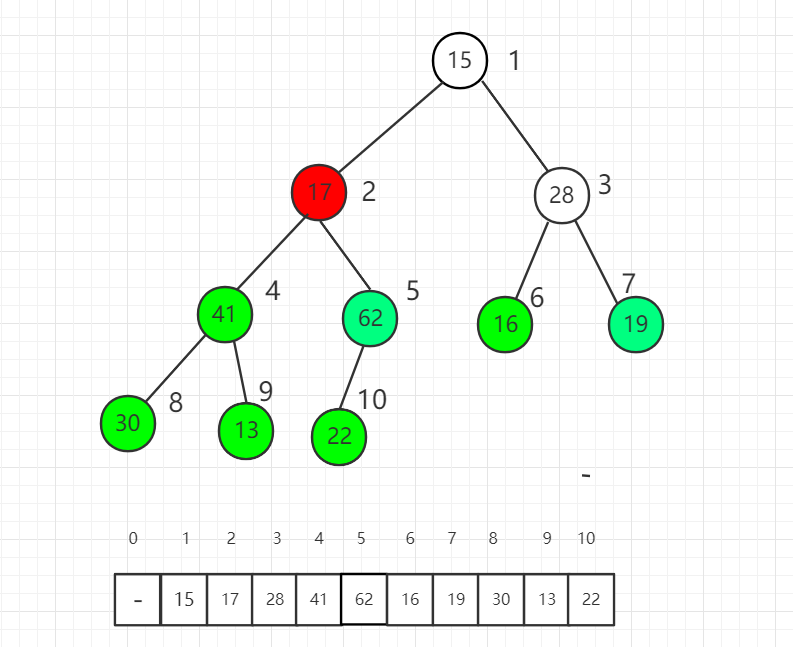
对索引 2 元素进行 shift down 操作

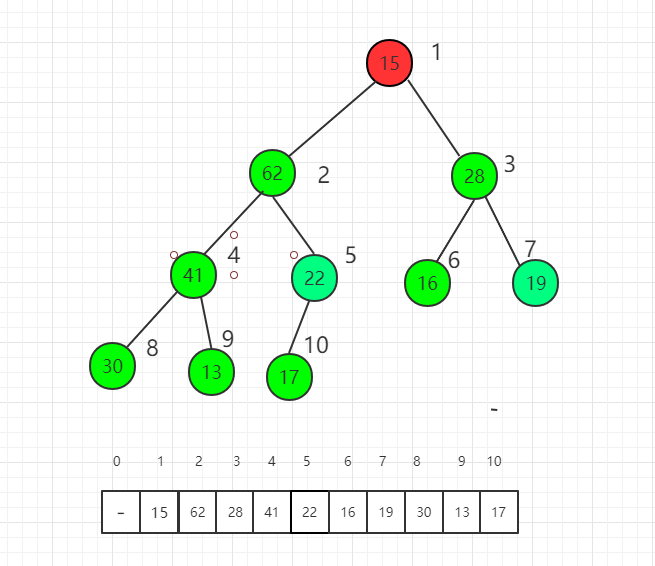
最后对根节点进行 shift down 操作，整个堆排序过程就完成了。

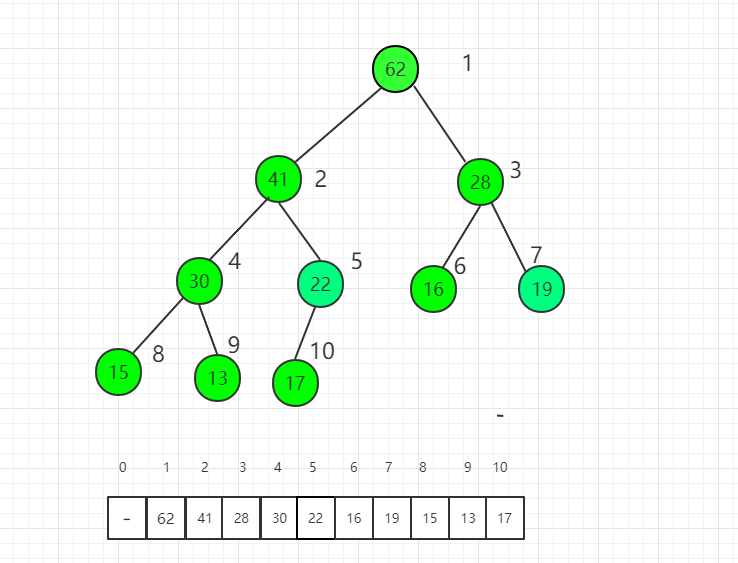
四、Java 实例代码

src/demo/heap/Heapify.java 文件代码：
package demo.heap;

import demo.sort.SortTestHelper;

/**
 * 用heapify进行堆排序
 */
public class Heapify<T extends Comparable> {

    protected T[] data;
    protected int count;
    protected int capacity;

    // 构造函数, 通过一个给定数组创建一个最大堆
    // 该构造堆的过程, 时间复杂度为O(n)
    public Heapify(T arr[]){

        int n = arr.length;

        data = (T[])new Comparable[n+1];
        capacity = n;

        for( int i = 0 ; i < n ; i ++ )
            data[i+1] = arr[i];
        count = n;
        //从第一个不是叶子节点的元素开始
        for( int i = count/2 ; i >= 1 ; i -- )
            shiftDown(i);
    }
    // 返回堆中的元素个数
    public int size(){
        return count;
    }
    // 返回一个布尔值, 表示堆中是否为空
    public boolean isEmpty(){
        return count == 0;
    }
    // 像最大堆中插入一个新的元素 item
    public void insert(T item){
        assert count + 1 <= capacity;
        data[count+1] = item;
        count ++;
        shiftUp(count);
    }
    // 从最大堆中取出堆顶元素, 即堆中所存储的最大数据
    public T extractMax(){
        assert count > 0;
        T ret = data[1];
        swap( 1 , count );
        count --;
        shiftDown(1);
        return ret;
    }
    // 获取最大堆中的堆顶元素
    public T getMax(){
        assert( count > 0 );
        return data[1];
    }


    // 交换堆中索引为i和j的两个元素
    private void swap(int i, int j){
        T t = data[i];
        data[i] = data[j];
        data[j] = t;
    }

    //********************
    //* 最大堆核心辅助函数
    //********************
    private void shiftUp(int k){

        while( k > 1 && data[k/2].compareTo(data[k]) < 0 ){
            swap(k, k/2);
            k /= 2;
        }
    }

    private void shiftDown(int k){

        while( 2*k <= count ){
            int j = 2*k; // 在此轮循环中,data[k]和data[j]交换位置
            if( j+1 <= count && data[j+1].compareTo(data[j]) > 0 )
                j ++;
            // data[j] 是 data[2*k]和data[2*k+1]中的最大值

            if( data[k].compareTo(data[j]) >= 0 ) break;
            swap(k, j);
            k = j;
        }
    }

    // 测试 heapify
    public static void main(String[] args) {
        int N = 100;
        Integer[] arr = SortTestHelper.generateRandomArray(N, 0, 100000);
        Heapify<Integer> heapify = new Heapify<Integer>(arr);
        // 将heapify中的数据逐渐使用extractMax取出来
        // 取出来的顺序应该是按照从大到小的顺序取出来的
        for( int i = 0 ; i < N ; i ++ ){
            arr[i] = heapify.extractMax();
            System.out.print(arr[i] + " ");
        }

        // 确保arr数组是从大到小排列的
        for( int i = 1 ; i < N ; i ++ )
            assert arr[i-1] >= arr[i];
    }
}

优化堆排序

上一节的堆排序，我们开辟了额外的空间进行构造堆和对堆进行排序。这一小节，我们进行优化，使用原地堆排序。

对于一个最大堆，首先将开始位置数据和数组末尾数值进行交换，那么数组末尾就是最大元素，然后再对W元素进行 shift down 操作，重新生成最大堆，然后将新生成的最大数和整个数组倒数第二位置进行交换，此时到处第二位置就是倒数第二大数据，这个过程以此类推。

整个过程可以用如下图表示：

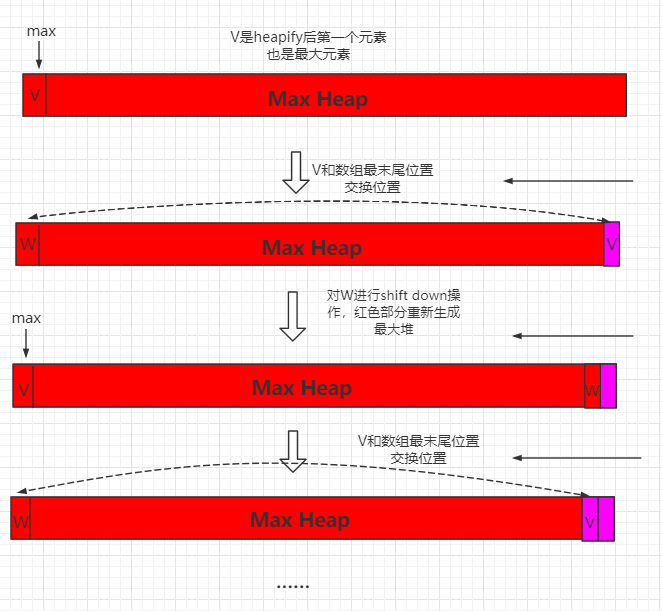
Java 实例代码

src/demo/heap/HeapSort.java 文件代码：
package demo.heap;

import demo.sort.SortTestHelper;

/**
 * 原地堆排序
 */
public class HeapSort<T extends Comparable> {


    public static void sort(Comparable[] arr) {

        int n = arr.length;

        // 注意，此时我们的堆是从0开始索引的
        // 从(最后一个元素的索引-1)/2开始
        // 最后一个元素的索引 = n-1
        for (int i = (n - 1 - 1) / 2; i >= 0; i--)
            shiftDown(arr, n, i);
       
        for (int i = n - 1; i > 0; i--) {
            swap(arr, 0, i);
            shiftDown(arr, i, 0);
        }
    }

    // 交换堆中索引为i和j的两个元素
    private static void swap(Object[] arr, int i, int j) {
        Object t = arr[i];
        arr[i] = arr[j];
        arr[j] = t;
    }

    // 原始的shiftDown过程
    private static void shiftDown(Comparable[] arr, int n, int k) {

        while (2 * k + 1 < n) {
            //左孩子节点
            int j = 2 * k + 1;
            //右孩子节点比左孩子节点大
            if (j + 1 < n && arr[j + 1].compareTo(arr[j]) > 0)
                j += 1;
            //比两孩子节点都大
            if (arr[k].compareTo(arr[j]) >= 0) break;
            //交换原节点和孩子节点的值
            swap(arr, k, j);
            k = j;
        }
    }

    // 测试 HeapSort
    public static void main(String[] args) {

        int N = 100;
        Integer[] arr = SortTestHelper.generateRandomArray(N, 0, 100000);
        sort(arr);
        // 将heapify中的数据逐渐使用extractMax取出来
        // 取出来的顺序应该是按照从大到小的顺序取出来的
        for (int i = 0; i < N; i++) {
            System.out.print(arr[i] + " ");
        }
        // 确保arr数组是从大到小排列的
        for (int i = 1; i < N; i++)
            assert arr[i - 1] >= arr[i];
    }
}

索引堆及其优化

一、概念及其介绍
索引堆是对堆这个数据结构的优化。

索引堆使用了一个新的 int 类型的数组，用于存放索引信息。

相较于堆，优点如下：

• 优化了交换元素的消耗。
• 加入的数据位置固定，方便寻找。

二、适用说明
如果堆中存储的元素较大，那么进行交换就要消耗大量的时间，这个时候可以用索引堆的数据结构进行替代，堆中存储的是数组的索引，我们相应操作的是索引。

三、结构图示

我们需要对之前堆的代码实现进行改造，换成直接操作索引的思维。首先构造函数添加索引数组属性 indexes。

protected T[] data;      // 最大索引堆中的数据
protected int[] indexes;    // 最大索引堆中的索引
protected int count;
protected int capacity;

相应构造函数调整为，添加初始化索引数组。

...
public IndexMaxHeap(int capacity){
    data = (T[])new Comparable[capacity+1];
    indexes = new int[capacity+1];
    count = 0;
    this.capacity = capacity;
}

…
调整插入操作，indexes 数组中添加的元素是真实 data 数组的索引 indexes[count+1] = i。

...
// 向最大索引堆中插入一个新的元素, 新元素的索引为i, 元素为item
// 传入的i对用户而言,是从0索引的
public void insert(int i, Item item){
    assert count + 1 <= capacity;
    assert i + 1 >= 1 && i + 1 <= capacity;
    i += 1;
    data[i] = item;
    indexes[count+1] = i;
    count ++;
    shiftUp(count);
}
...

调整 shift up 操作：比较的是 data 数组中父节点数据的大小，所以需要表示为 data[index[k/2]] < data[indexs[k]]，交换 index 数组的索引，对 data 数组不产生任何变动，shift down 同理。

...
//k是堆的索引
// 索引堆中, 数据之间的比较根据data的大小进行比较, 但实际操作的是索引
private void shiftUp(int k){

    while( k > 1 && data[indexes[k/2]].compareTo(data[indexes[k]]) < 0 ){
        swapIndexes(k, k/2);
        k /= 2;
    }
}
...

从索引堆中取出元素，对大元素为根元素 data[index[1]] 中的数据，然后再交换索引位置进行 shift down 操作。

...
public T extractMax(){
    assert count > 0;
    T ret = data[indexes[1]];
    swapIndexes( 1 , count );
    count --;
    shiftDown(1);
    return ret;
}
...

也可以直接取出最大值的 data 数组索引值

...
// 从最大索引堆中取出堆顶元素的索引
public int extractMaxIndex(){
    assert count > 0;
    int ret = indexes[1] - 1;
    swapIndexes( 1 , count );
    count --;
    shiftDown(1);
    return ret;
}
...

修改索引位置数据

...
// 将最大索引堆中索引为i的元素修改为newItem
public void change( int i , Item newItem ){
    i += 1;
    data[i] = newItem;
    // 找到indexes[j] = i, j表示data[i]在堆中的位置
    // 之后shiftUp(j), 再shiftDown(j)
    for( int j = 1 ; j <= count ; j ++ )
        if( indexes[j] == i ){
            shiftUp(j);
            shiftDown(j);
            return;
        }
}
...

四、Java 实例代码

src/demo/heap/IndexMaxHeap.java 文件代码：
package demo.heap;

import java.util.Arrays;

/**
 * 索引堆
 */
// 最大索引堆，思路：元素比较的是data数据,元素交换的是索引
public class IndexMaxHeap<T extends Comparable> {

    protected T[] data;      // 最大索引堆中的数据
    protected int[] indexes;    // 最大索引堆中的索引
    protected int count;
    protected int capacity;

    // 构造函数, 构造一个空堆, 可容纳capacity个元素
    public IndexMaxHeap(int capacity){
        data = (T[])new Comparable[capacity+1];
        indexes = new int[capacity+1];
        count = 0;
        this.capacity = capacity;
    }

    // 返回索引堆中的元素个数
    public int size(){
        return count;
    }

    // 返回一个布尔值, 表示索引堆中是否为空
    public boolean isEmpty(){
        return count == 0;
    }

    // 向最大索引堆中插入一个新的元素, 新元素的索引为i, 元素为item
    // 传入的i对用户而言,是从0索引的
    public void insert(int i, T item){

        assert count + 1 <= capacity;
        assert i + 1 >= 1 && i + 1 <= capacity;

        i += 1;
        data[i] = item;
        indexes[count+1] = i;
        count ++;



        shiftUp(count);
    }

    // 从最大索引堆中取出堆顶元素, 即索引堆中所存储的最大数据
    public T extractMax(){
        assert count > 0;

        T ret = data[indexes[1]];
        swapIndexes( 1 , count );
        count --;
        shiftDown(1);

        return ret;
    }

    // 从最大索引堆中取出堆顶元素的索引
    public int extractMaxIndex(){
        assert count > 0;

        int ret = indexes[1] - 1;
        swapIndexes( 1 , count );
        count --;
        shiftDown(1);

        return ret;
    }

    // 获取最大索引堆中的堆顶元素
    public T getMax(){
        assert count > 0;
        return data[indexes[1]];
    }

    // 获取最大索引堆中的堆顶元素的索引
    public int getMaxIndex(){
        assert count > 0;
        return indexes[1]-1;
    }

    // 获取最大索引堆中索引为i的元素
    public T getItem( int i ){
        assert i + 1 >= 1 && i + 1 <= capacity;
        return data[i+1];
    }

    // 将最大索引堆中索引为i的元素修改为newItem
    public void change( int i , T newItem ){
        i += 1;
        data[i] = newItem;
        // 找到indexes[j] = i, j表示data[i]在堆中的位置
        // 之后shiftUp(j), 再shiftDown(j)
        for( int j = 1 ; j <= count ; j ++ )
            if( indexes[j] == i ){
                shiftUp(j);
                shiftDown(j);
                return;
            }
    }

    // 交换索引堆中的索引i和j
    private void swapIndexes(int i, int j){
        int t = indexes[i];
        indexes[i] = indexes[j];
        indexes[j] = t;
    }

    //********************
    //* 最大索引堆核心辅助函数
    //********************
    //k是堆的索引
    // 索引堆中, 数据之间的比较根据data的大小进行比较, 但实际操作的是索引
    private void shiftUp(int k){

        while( k > 1 && data[indexes[k/2]].compareTo(data[indexes[k]]) < 0 ){
            swapIndexes(k, k/2);
            k /= 2;
        }
    }

    // 索引堆中, 数据之间的比较根据data的大小进行比较, 但实际操作的是索引
    private void shiftDown(int k){

        while( 2*k <= count ){
            int j = 2*k;
            if( j+1 <= count && data[indexes[j+1]].compareTo(data[indexes[j]]) > 0 )
                j ++;

            if( data[indexes[k]].compareTo(data[indexes[j]]) >= 0 )
                break;

            swapIndexes(k, j);
            k = j;
        }
    }

    // 测试 IndexMaxHeap
    public static void main(String[] args) {

        int N = 1000000;
        IndexMaxHeap<Integer> indexMaxHeap = new IndexMaxHeap<Integer>(N);
        for( int i = 0 ; i < N ; i ++ )
            indexMaxHeap.insert( i , (int)(Math.random()*N) );
 
    }
}

上述修改索引位置在查找索引位置我们使用了遍历，效率不高。我们还可以再优化一遍，维护一组 reverse[i] 数组，表示索引 i 在 indexes(堆) 中的位置，把查找的时间复杂度降为 O(1)。

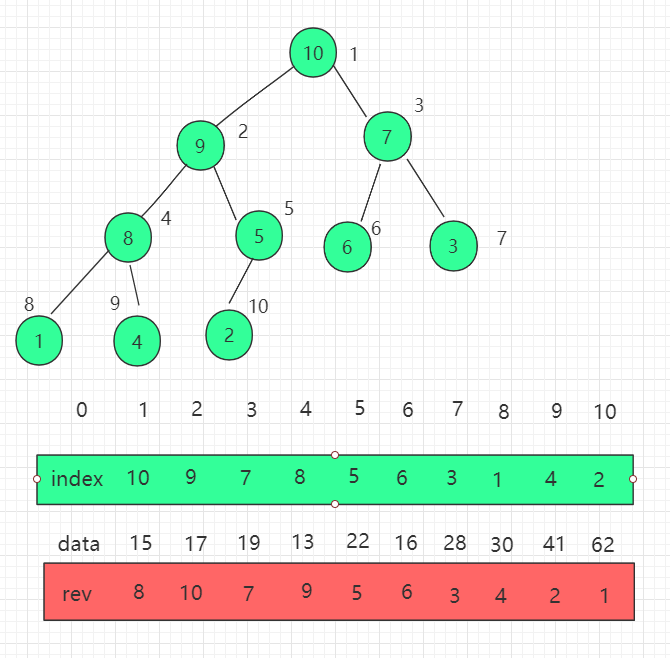
有如下性质：

indexes[i] = j
reverse[j] = i

indexes[reverse[i]] = i
reverse[indexes[i]] = i

二分搜索树

二分搜索树

一、概念及其介绍
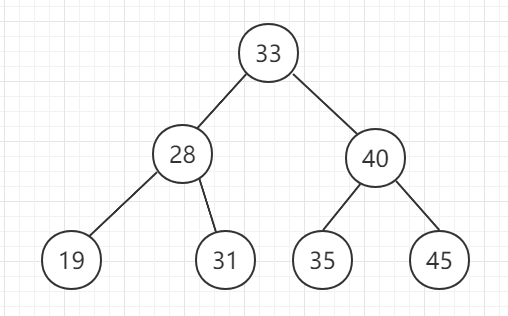
二分搜索树（英语：Binary Search Tree），也称为 二叉查找树 、二叉搜索树 、有序二叉树或排序二叉树。满足以下几个条件：

• 若它的左子树不为空，左子树上所有节点的值都小于它的根节点。
• 若它的右子树不为空，右子树上所有的节点的值都大于它的根节点。

它的左、右子树也都是二分搜索树。

如下图所示：

二、适用说明
二分搜索树有着高效的插入、删除、查询操作。

平均时间的时间复杂度为 O(log n)，最差情况为 O(n)。二分搜索树与堆不同，不一定是完全二叉树，底层不容易直接用数组表示故采用链表来实现二分搜索树。

	插入元素	删除元素	查找元素
普通数组	O(n)	O(n)	O(n)
顺序数组	O(logn)	O(n)	O(n)
二分搜索树	O(logn)	O(logn)	O(logn)

下面先介绍数组形式的二分查找法作为思想的借鉴，后面继续介绍二分搜索树的查找方式。

三、二分查找法过程图示
二分查找法的思想在 1946 年提出，查找问题是计算机中非常重要的基础问题，对于有序数列，才能使用二分查找法。如果我们要查找一元素，先看数组中间的值V和所需查找数据的大小关系，分三种情况：

1、等于所要查找的数据，直接找到
2、若小于 V，在小于 V 部分分组继续查询
2、若大于 V，在大于 V 部分分组继续查询

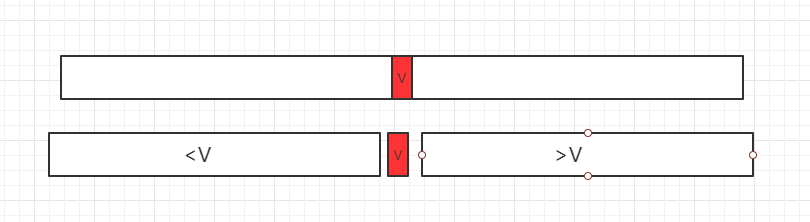
四、Java 实例代码

src/demo/binary/BinarySearch.java 文件代码：
package demo.binarySearch;

/**
 * 二分查找法
 */
public class BinarySearch
    // 二分查找法,在有序数组arr中,查找target
    // 如果找到target,返回相应的索引index
    // 如果没有找到target,返回-1
    public static int find(Comparable[] arr, Comparable target) {

        // 在arr[l...r]之中查找target
        int l = 0, r = arr.length-1;
        while( l <= r ){

            //int mid = (l + r)/2;
            // 防止极端情况下的整形溢出，使用下面的逻辑求出mid
            int mid = l + (r-l)/2;

            if( arr[mid].compareTo(target) == 0 )
                return mid;

            if( arr[mid].compareTo(target) > 0 )
                r = mid - 1;
            else
                l = mid + 1;
        }

        return -1;
    }
}

二分搜索树节点的插入

首先定义一个二分搜索树，Java 代码表示如下:

public class BST<Key extends Comparable<Key>, Value> {

    // 树中的节点为私有的类, 外界不需要了解二分搜索树节点的具体实现
    private class Node {
        private Key key;
        private Value value;
        private Node left, right;

        public Node(Key key, Value value) {
            this.key = key;
            this.value = value;
            left = right = null;
        }
    }
    // 根节点
    private Node root;
    // 树种的节点个数
    private int count;
    // 构造函数, 默认构造一棵空二分搜索树
    public BST() {
        root = null;
        count = 0;
    }
    // 返回二分搜索树的节点个数
    public int size() {
        return count;
    }
    // 返回二分搜索树是否为空
    public boolean isEmpty() {
        return count == 0;
    }
}

Node 表示节点，count 代表节点的数量。

以下实例向如下二分搜索树中插入元素 61 的步骤：

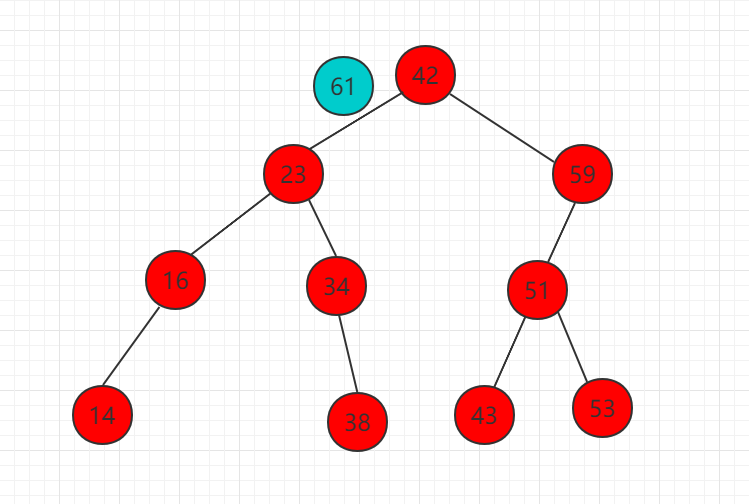
（1）需要插入的元素 61 比 42 大，比较 42 的右子树根节点。

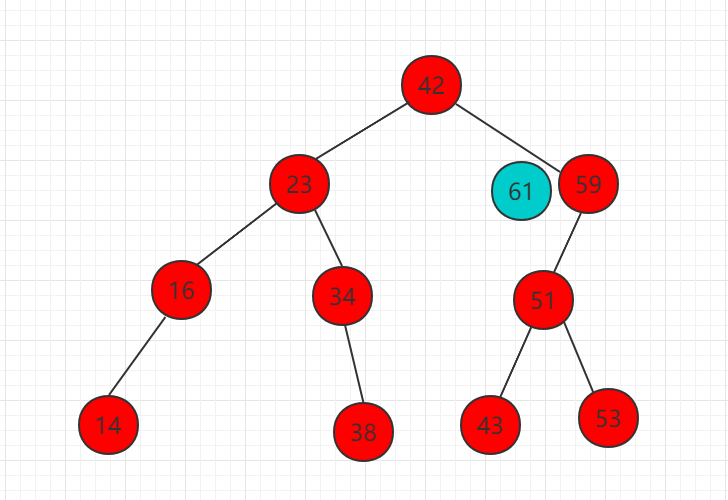
（2）61 比 59 大，所以需要把 61 移动到 59 右子树相应位置，而此时为空，直接插入作为 59 的右子节点。

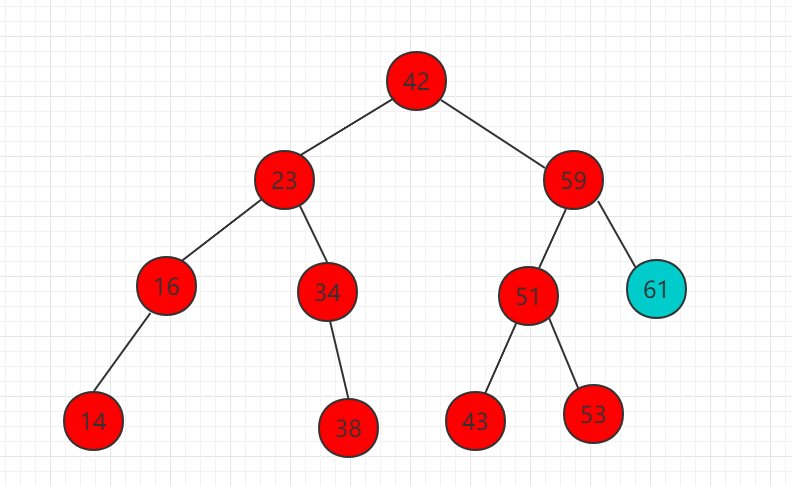
插入操作也是一个递归过程，分三种情况，等于、大于、小于。

Java 实例代码

src/demo/binary/BinarySearchTreeInsert.java 文件代码：
package demo.binary;

/**
 * 二分搜索树插入新的元素
 */

public class BinarySearchTreeInsert<Key extends Comparable<Key>, Value> {

    // 树中的节点为私有的类, 外界不需要了解二分搜索树节点的具体实现
    private class Node {
        private Key key;
        private Value value;
        private Node left, right;

        public Node(Key key, Value value) {
            this.key = key;
            this.value = value;
            left = right = null;
        }
    }

    private Node root;  // 根节点
    private int count;  // 树种的节点个数

    // 构造函数, 默认构造一棵空二分搜索树
    public BinarySearchTreeInsert() {
        root = null;
        count = 0;
    }

    // 返回二分搜索树的节点个数
    public int size() {
        return count;
    }

    // 返回二分搜索树是否为空
    public boolean isEmpty() {
        return count == 0;
    }

    // 向二分搜索树中插入一个新的(key, value)数据对
    public void insert(Key key, Value value) {
        root = insert(root, key, value);
    }

    //核心代码---开始
    // 向以node为根的二分搜索树中, 插入节点(key, value), 使用递归算法
    // 返回插入新节点后的二分搜索树的根
    private Node insert(Node node, Key key, Value value) {
        if (node == null) {
            count++;
            return new Node(key, value);
        }
        if (key.compareTo(node.key) == 0)
            node.value = value;
        else if (key.compareTo(node.key) < 0)
            node.left = insert(node.left, key, value);
        else    // key > node->key
            node.right = insert(node.right, key, value);

        return node;
    }
    //核心代码---结束
}

二分搜索树节点的查找

二分搜索树没有下标, 所以针对二分搜索树的查找操作, 这里定义一个 contain 方法, 判断二分搜索树是否包含某个元素, 返回一个布尔型变量, 这个查找的操作一样是一个递归的过程, 具体代码实现如下:

...
// 查看以node为根的二分搜索树中是否包含键值为key的节点, 使用递归算法
private boolean contain(Node node, Key key){

    if( node == null )
        return false;

    if( key.compareTo(node.key) == 0 )
        return true;
    else if( key.compareTo(node.key) < 0 )
        return contain( node.left , key );
    else // key > node->key
        return contain( node.right , key );
}
...

以下实例在二分搜索树中寻找 43 元素

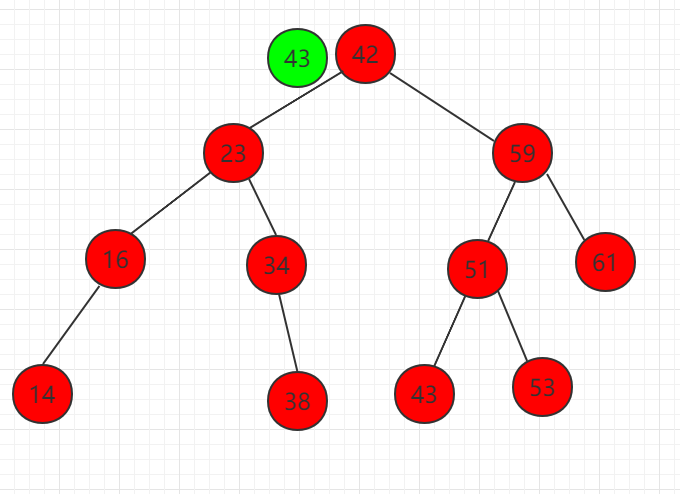
(1) 元素 43 比根节点 42 大，需要在右子节点继续比较。

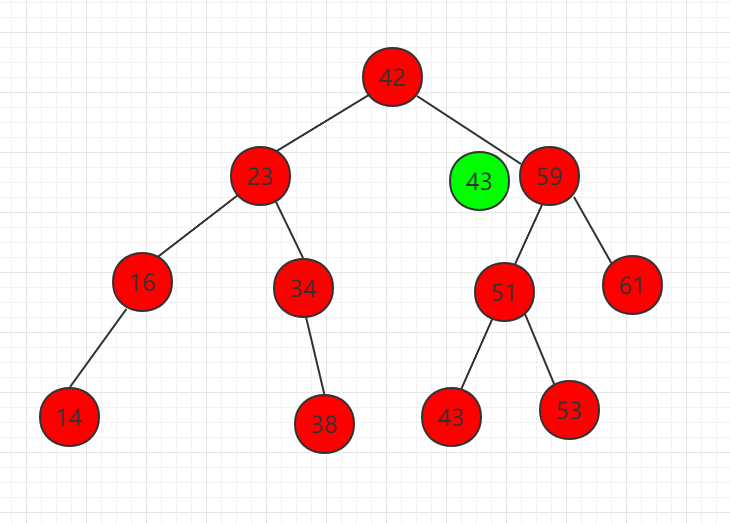
(2) 元素 43 比 59 小，需要在左子节点继续比较。

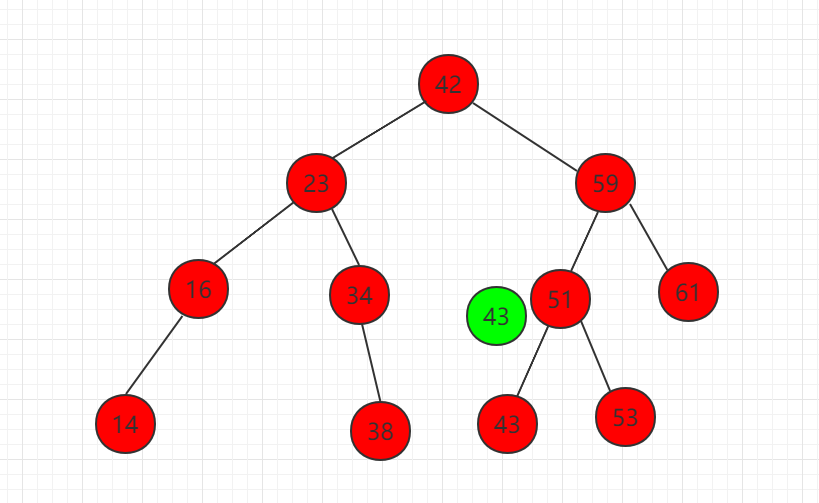
(3) 元素 43 比 51 小，需要在左子节点继续比较。

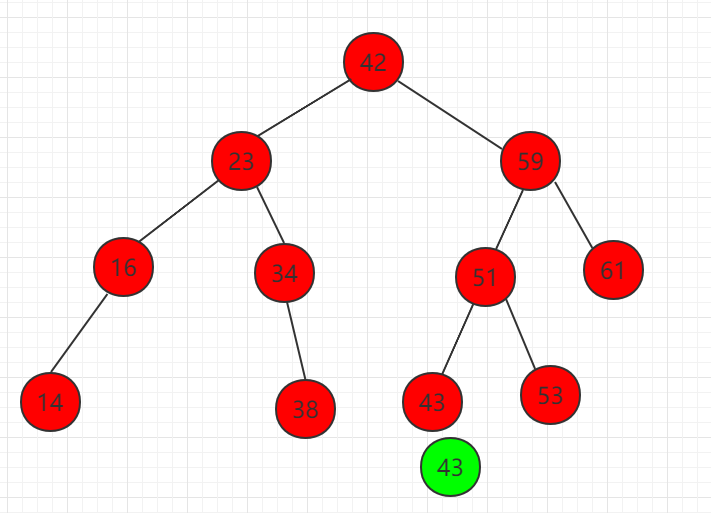
(4) 查找 51 的左子节点 43，正好和相等，结束。

如果需要查找 key 对应的 value，代码如下所示:

...
// 在以node为根的二分搜索树中查找key所对应的value, 递归算法
// 若value不存在, 则返回NULL
private Value search(Node node, Key key){

    if( node == null )
        return null;

    if( key.compareTo(node.key) == 0 )
        return node.value;
    else if( key.compareTo(node.key) < 0 )
        return search( node.left , key );
    else // key > node->key
        return search( node.right, key );
}
...

Java 实例代码

src/demo/binary/BinarySearchTreeSearch.java 文件代码：
package demo.binary;

/**
 * 二分搜索树查找
 */
public class BinarySearchTreeSearch<Key extends Comparable<Key>, Value> {
    // 树中的节点为私有的类, 外界不需要了解二分搜索树节点的具体实现
    private class Node {
        private Key key;
        private Value value;
        private Node left, right;

        public Node(Key key, Value value) {
            this.key = key;
            this.value = value;
            left = right = null;
        }
    }
    // 根节点
    private Node root;
    // 树种的节点个数
    private int count;

    // 构造函数, 默认构造一棵空二分搜索树
    public BinarySearchTreeSearch() {
        root = null;
        count = 0;
    }

    // 返回二分搜索树的节点个数
    public int size() {
        return count;
    }

    // 返回二分搜索树是否为空
    public boolean isEmpty() {
        return count == 0;
    }

    // 向二分搜索树中插入一个新的(key, value)数据对
    public void insert(Key key, Value value){
        root = insert(root, key, value);
    }

    // 查看二分搜索树中是否存在键key
    public boolean contain(Key key){
        return contain(root, key);
    }

    // 在二分搜索树中搜索键key所对应的值。如果这个值不存在, 则返回null
    public Value search(Key key){
        return search( root , key );
    }


    //********************
    //* 二分搜索树的辅助函数
    //********************

    // 向以node为根的二分搜索树中, 插入节点(key, value), 使用递归算法
    // 返回插入新节点后的二分搜索树的根
    private Node insert(Node node, Key key, Value value){

        if( node == null ){
            count ++;
            return new Node(key, value);
        }

        if( key.compareTo(node.key) == 0 )
            node.value = value;
        else if( key.compareTo(node.key) < 0 )
            node.left = insert( node.left , key, value);
        else    // key > node->key
            node.right = insert( node.right, key, value);

        return node;
    }

    // 查看以node为根的二分搜索树中是否包含键值为key的节点, 使用递归算法
    private boolean contain(Node node, Key key){

        if( node == null )
            return false;

        if( key.compareTo(node.key) == 0 )
            return true;
        else if( key.compareTo(node.key) < 0 )
            return contain( node.left , key );
        else // key > node->key
            return contain( node.right , key );
    }

    // 在以node为根的二分搜索树中查找key所对应的value, 递归算法
    // 若value不存在, 则返回NULL
    private Value search(Node node, Key key){

        if( node == null )
            return null;

        if( key.compareTo(node.key) == 0 )
            return node.value;
        else if( key.compareTo(node.key) < 0 )
            return search( node.left , key );
        else // key > node->key
            return search( node.right, key );
    }
}

二分搜索树深度优先遍历

二分搜索树遍历分为两大类，深度优先遍历和层序遍历。

深度优先遍历分为三种：先序遍历（preorder tree walk）、中序遍历（inorder tree walk）、后序遍历（postorder tree walk），分别为：

1、前序遍历：先访问当前节点，再依次递归访问左右子树。
2、中序遍历：先递归访问左子树，再访问自身，再递归访问右子树。
3、后序遍历：先递归访问左右子树，再访问自身节点。
前序遍历结果图示：

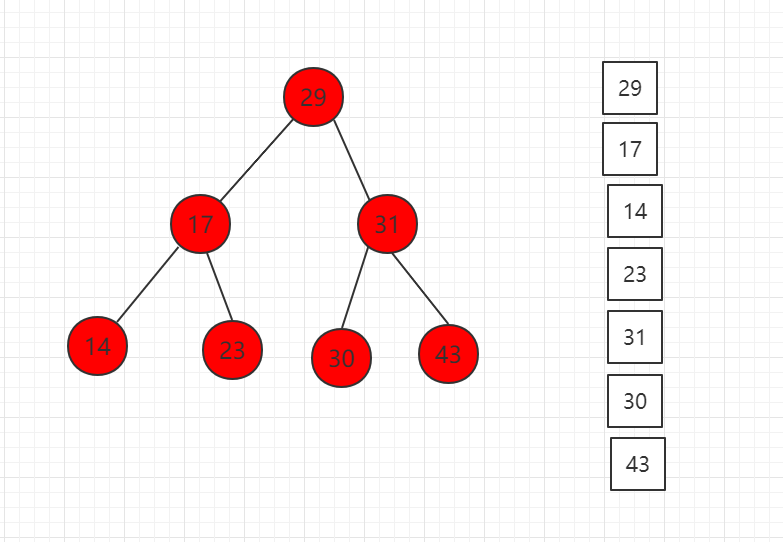
对应代码示例：

...
// 对以node为根的二叉搜索树进行前序遍历, 递归算法
private void preOrder(Node node){

    if( node != null ){
        System.out.println(node.key);
        preOrder(node.left);
        preOrder(node.right);
    }
}
...

中序遍历结果图示：

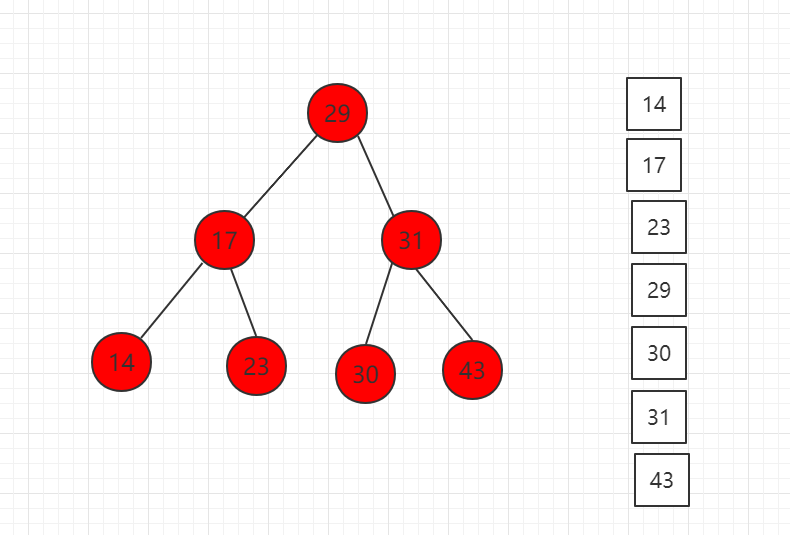
对应代码示例：

...
// 对以node为根的二叉搜索树进行中序遍历, 递归算法
private void inOrder(Node node){

    if( node != null ){
        inOrder(node.left);
        System.out.println(node.key);
        inOrder(node.right);
    }
}
...

后序遍历结果图示：

对应代码示例：

...
// 对以node为根的二叉搜索树进行后序遍历, 递归算法
private void postOrder(Node node){

    if( node != null ){
        postOrder(node.left);
        postOrder(node.right);
        System.out.println(node.key);
    }
}
...

Java 实例代码

src/demo/binary/Traverse.java 文件代码：
package demo.binary;

/**
 * 优先遍历
 */

public class Traverse<Key extends Comparable<Key>, Value>  {

    // 树中的节点为私有的类, 外界不需要了解二分搜索树节点的具体实现
    private class Node {
        private Key key;
        private Value value;
        private Node left, right;

        public Node(Key key, Value value) {
            this.key = key;
            this.value = value;
            left = right = null;
        }
    }

    private Node root;  // 根节点
    private int count;  // 树种的节点个数

    // 构造函数, 默认构造一棵空二分搜索树
    public Traverse() {
        root = null;
        count = 0;
    }

    // 返回二分搜索树的节点个数
    public int size() {
        return count;
    }

    // 返回二分搜索树是否为空
    public boolean isEmpty() {
        return count == 0;
    }

    // 向二分搜索树中插入一个新的(key, value)数据对
    public void insert(Key key, Value value){
        root = insert(root, key, value);
    }

    // 查看二分搜索树中是否存在键key
    public boolean contain(Key key){
        return contain(root, key);
    }

    // 在二分搜索树中搜索键key所对应的值。如果这个值不存在, 则返回null
    public Value search(Key key){
        return search( root , key );
    }

    // 二分搜索树的前序遍历
    public void preOrder(){
        preOrder(root);
    }

    // 二分搜索树的中序遍历
    public void inOrder(){
        inOrder(root);
    }

    // 二分搜索树的后序遍历
    public void postOrder(){
        postOrder(root);
    }

    //********************
    //* 二分搜索树的辅助函数
    //********************

    // 向以node为根的二分搜索树中, 插入节点(key, value), 使用递归算法
    // 返回插入新节点后的二分搜索树的根
    private Node insert(Node node, Key key, Value value){

        if( node == null ){
            count ++;
            return new Node(key, value);
        }

        if( key.compareTo(node.key) == 0 )
            node.value = value;
        else if( key.compareTo(node.key) < 0 )
            node.left = insert( node.left , key, value);
        else    // key > node->key
            node.right = insert( node.right, key, value);

        return node;
    }

    // 查看以node为根的二分搜索树中是否包含键值为key的节点, 使用递归算法
    private boolean contain(Node node, Key key){

        if( node == null )
            return false;

        if( key.compareTo(node.key) == 0 )
            return true;
        else if( key.compareTo(node.key) < 0 )
            return contain( node.left , key );
        else // key > node->key
            return contain( node.right , key );
    }

    // 在以node为根的二分搜索树中查找key所对应的value, 递归算法
    // 若value不存在, 则返回NULL
    private Value search(Node node, Key key){

        if( node == null )
            return null;

        if( key.compareTo(node.key) == 0 )
            return node.value;
        else if( key.compareTo(node.key) < 0 )
            return search( node.left , key );
        else // key > node->key
            return search( node.right, key );
    }

    // 对以node为根的二叉搜索树进行前序遍历, 递归算法
    private void preOrder(Node node){

        if( node != null ){
            System.out.println(node.key);
            preOrder(node.left);
            preOrder(node.right);
        }
    }

    // 对以node为根的二叉搜索树进行中序遍历, 递归算法
    private void inOrder(Node node){

        if( node != null ){
            inOrder(node.left);
            System.out.println(node.key);
            inOrder(node.right);
        }
    }

    // 对以node为根的二叉搜索树进行后序遍历, 递归算法
    private void postOrder(Node node){

        if( node != null ){
            postOrder(node.left);
            postOrder(node.right);
            System.out.println(node.key);
        }
    }
}

二分搜索树层序遍历

二分搜索树的层序遍历，即逐层进行遍历，即将每层的节点存在队列当中，然后进行出队（取出节点）和入队（存入下一层的节点）的操作，以此达到遍历的目的。

通过引入一个队列来支撑层序遍历：

• 如果根节点为空，无可遍历；

• 如果根节点不为空：

  先将根节点入队；
  只要队列不为空：

  • 出队队首节点，并遍历；
  • 如果队首节点有左孩子，将左孩子入队；
  • 如果队首节点有右孩子，将右孩子入队；

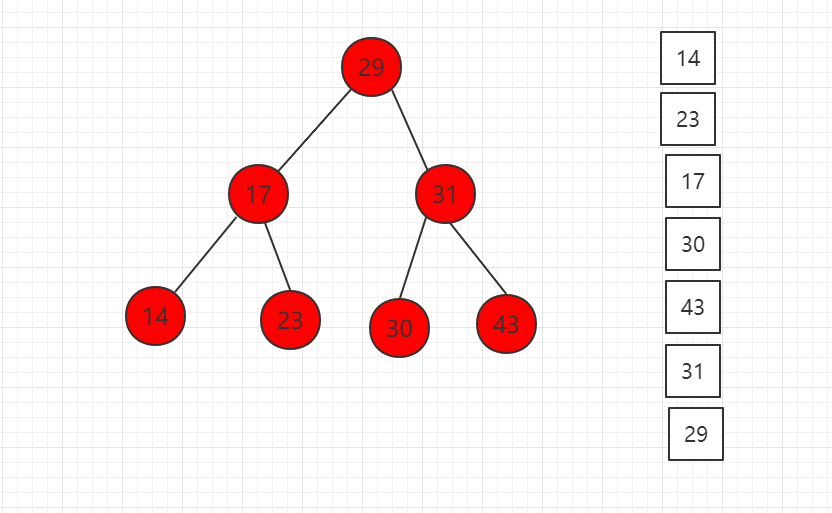
下面依次演示如下步骤：

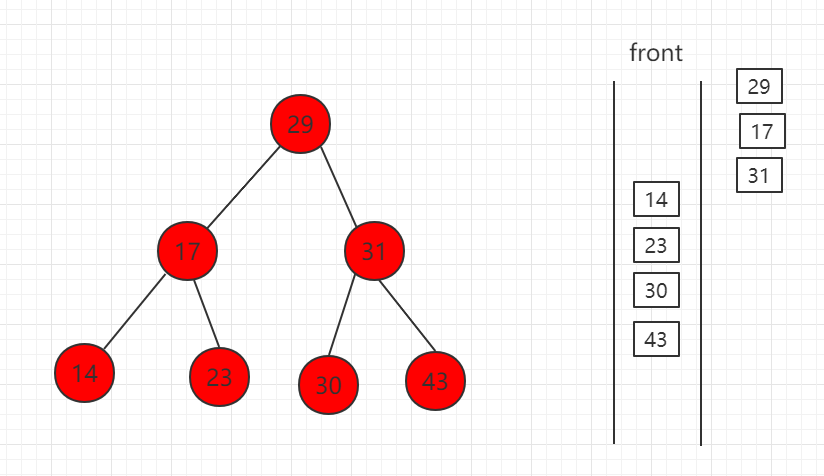
（1）先取出根节点放入队列

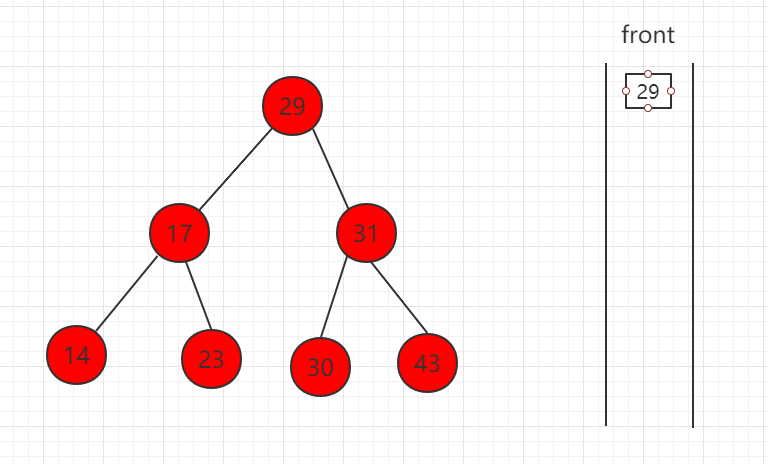
（2）取出 29，左右孩子节点入队

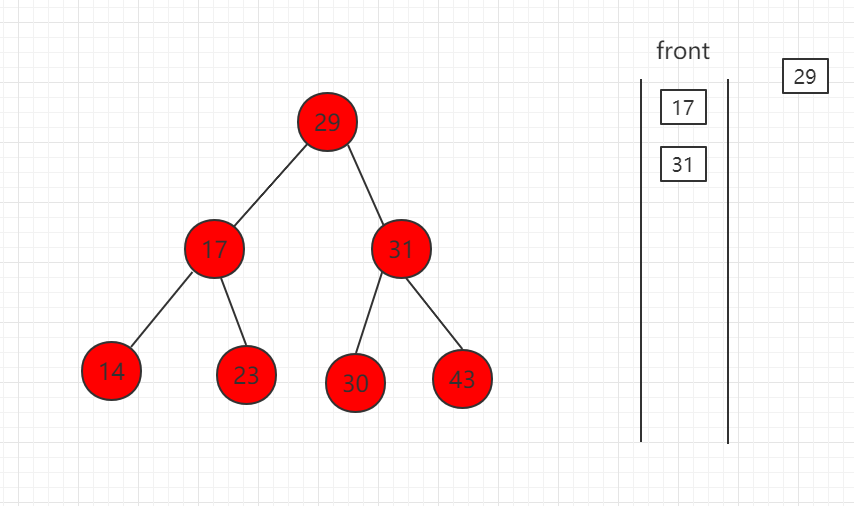
（3）队首 17 出队，孩子节点 14、23 入队。

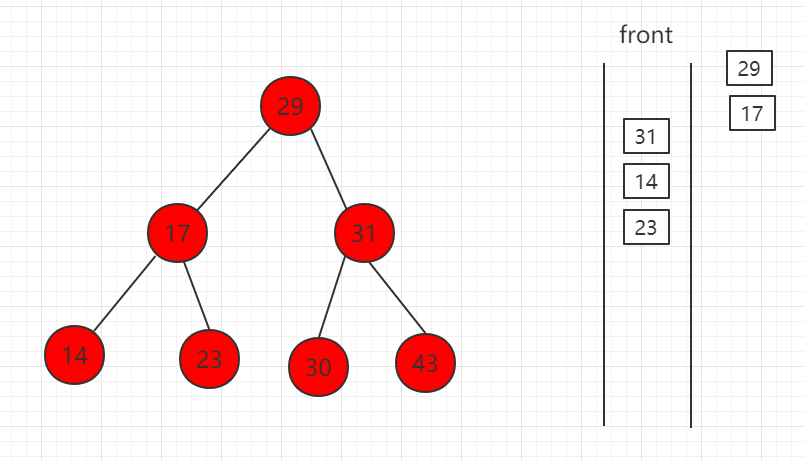
（4）31 出队，孩子节点 30 和 43 入队

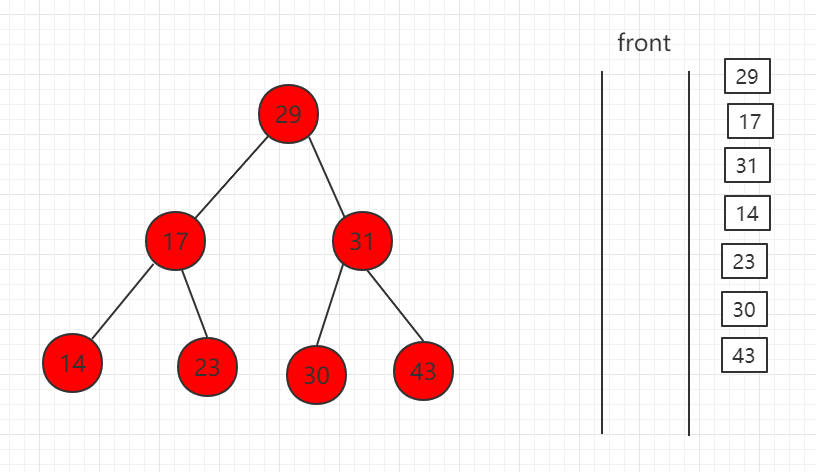
（5）最后全部出队

核心代码示例：

...
// 二分搜索树的层序遍历
public void levelOrder(){

    // 我们使用LinkedList来作为我们的队列
    LinkedList<Node> q = new LinkedList<Node>();
    q.add(root);
    while( !q.isEmpty() ){

        Node node = q.remove();

        System.out.println(node.key);

        if( node.left != null )
            q.add( node.left );
        if( node.right != null )
            q.add( node.right );
    }
}
...

Java 实例代码

src/demo/binary/LevelTraverse.java 文件代码：
package demo.binary;

import java.util.LinkedList;

/**
 * 层序遍历
 */
public class LevelTraverse<Key extends Comparable<Key>, Value>{

    // 树中的节点为私有的类, 外界不需要了解二分搜索树节点的具体实现
    private class Node {
        private Key key;
        private Value value;
        private Node left, right;

        public Node(Key key, Value value) {
            this.key = key;
            this.value = value;
            left = right = null;
        }
    }

    private Node root;  // 根节点
    private int count;  // 树种的节点个数

    // 构造函数, 默认构造一棵空二分搜索树
    public LevelTraverse() {
        root = null;
        count = 0;
    }

    // 返回二分搜索树的节点个数
    public int size() {
        return count;
    }

    // 返回二分搜索树是否为空
    public boolean isEmpty() {
        return count == 0;
    }

    // 向二分搜索树中插入一个新的(key, value)数据对
    public void insert(Key key, Value value){
        root = insert(root, key, value);
    }

    // 查看二分搜索树中是否存在键key
    public boolean contain(Key key){
        return contain(root, key);
    }

    // 在二分搜索树中搜索键key所对应的值。如果这个值不存在, 则返回null
    public Value search(Key key){
        return search( root , key );
    }

    // 二分搜索树的前序遍历
    public void preOrder(){
        preOrder(root);
    }

    // 二分搜索树的中序遍历
    public void inOrder(){
        inOrder(root);
    }

    // 二分搜索树的后序遍历
    public void postOrder(){
        postOrder(root);
    }

    // 二分搜索树的层序遍历
    public void levelOrder(){

        // 我们使用LinkedList来作为我们的队列
        LinkedList<Node> q = new LinkedList<Node>();
        q.add(root);
        while( !q.isEmpty() ){

            Node node = q.remove();

            System.out.println(node.key);

            if( node.left != null )
                q.add( node.left );
            if( node.right != null )
                q.add( node.right );
        }
    }

    //********************
    //* 二分搜索树的辅助函数
    //********************

    // 向以node为根的二分搜索树中, 插入节点(key, value), 使用递归算法
    // 返回插入新节点后的二分搜索树的根
    private Node insert(Node node, Key key, Value value){

        if( node == null ){
            count ++;
            return new Node(key, value);
        }

        if( key.compareTo(node.key) == 0 )
            node.value = value;
        else if( key.compareTo(node.key) < 0 )
            node.left = insert( node.left , key, value);
        else    // key > node->key
            node.right = insert( node.right, key, value);

        return node;
    }

    // 查看以node为根的二分搜索树中是否包含键值为key的节点, 使用递归算法
    private boolean contain(Node node, Key key){

        if( node == null )
            return false;

        if( key.compareTo(node.key) == 0 )
            return true;
        else if( key.compareTo(node.key) < 0 )
            return contain( node.left , key );
        else // key > node->key
            return contain( node.right , key );
    }

    // 在以node为根的二分搜索树中查找key所对应的value, 递归算法
    // 若value不存在, 则返回NULL
    private Value search(Node node, Key key){

        if( node == null )
            return null;

        if( key.compareTo(node.key) == 0 )
            return node.value;
        else if( key.compareTo(node.key) < 0 )
            return search( node.left , key );
        else // key > node->key
            return search( node.right, key );
    }

    // 对以node为根的二叉搜索树进行前序遍历, 递归算法
    private void preOrder(Node node){

        if( node != null ){
            System.out.println(node.key);
            preOrder(node.left);
            preOrder(node.right);
        }
    }

    // 对以node为根的二叉搜索树进行中序遍历, 递归算法
    private void inOrder(Node node){

        if( node != null ){
            inOrder(node.left);
            System.out.println(node.key);
            inOrder(node.right);
        }
    }

    // 对以node为根的二叉搜索树进行后序遍历, 递归算法
    private void postOrder(Node node){

        if( node != null ){
            postOrder(node.left);
            postOrder(node.right);
            System.out.println(node.key);
        }
    }
   
}

二分搜索树节点删除

本小节介绍二分搜索树节点的删除之前，先介绍如何查找最小值和最大值，以及删除最小值和最大值。

以最小值为例（最大值同理）：

查找最小 key 值代码逻辑，往左子节点递归查找下去：

...
// 返回以node为根的二分搜索树的最小键值所在的节点
private Node minimum(Node node){
    if( node.left == null )
        return node;

    return minimum(node.left);
}
...

删除二分搜索树的最小 key 值，如果该节点没有右子树，那么直接删除，如果存在右子树，如图所示：

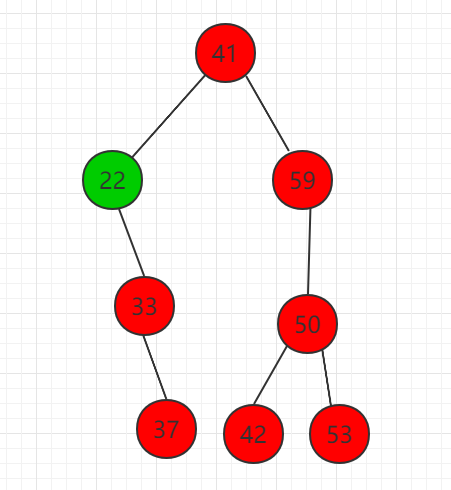
删除节点 22，存在右孩子，只需要将右子树 33 节点代替节点 22。

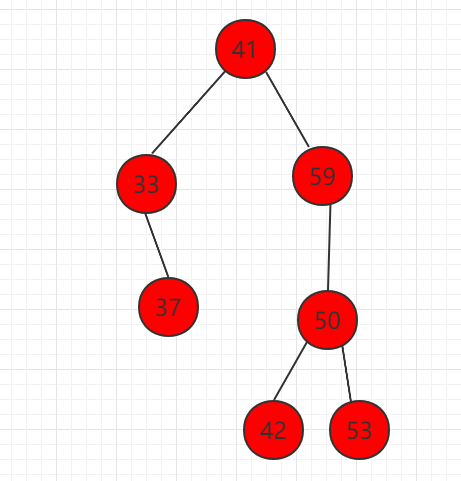
这个删除最小值用代码表示:

...
// 删除掉以node为根的二分搜索树中的最小节点
// 返回删除节点后新的二分搜索树的根
private Node removeMin(Node node){

    if( node.left == null ){

        Node rightNode = node.right;
        node.right = null;
        count --;
        return rightNode;
    }

    node.left = removeMin(node.left);
    return node;
}
...

现在讨论二分搜索树节点删除分以下三种情况：

1、删除只有左孩子的节点，如下图节点 58。

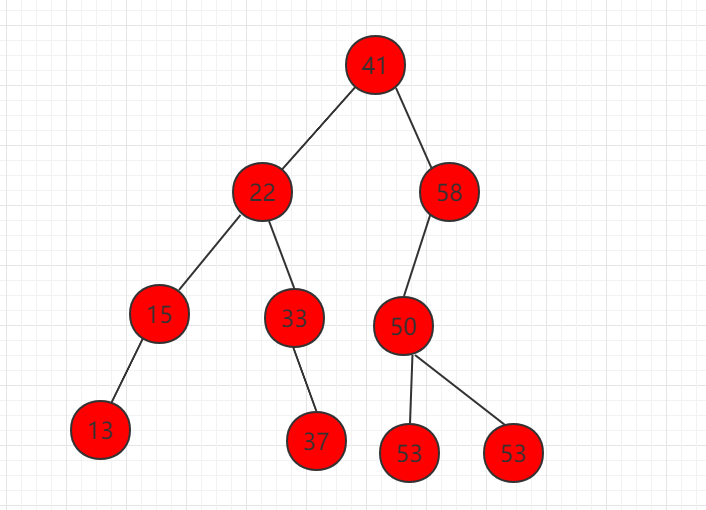
删除掉元素 58，让左子树直接代替 58 的位置，整个二分搜索树的性质不变。

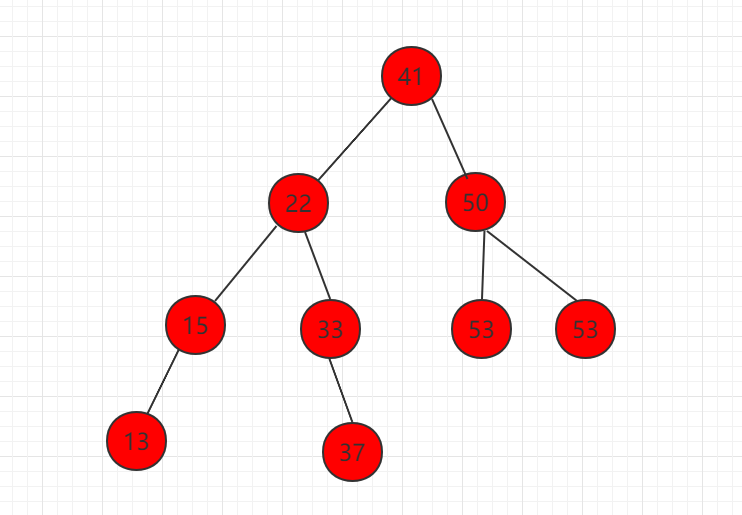
2、删除只有右孩子的节点，如下图节点 58。

删除掉元素 58，让右子树直接代替 58 的位置，整个二分搜索树的性质不变。

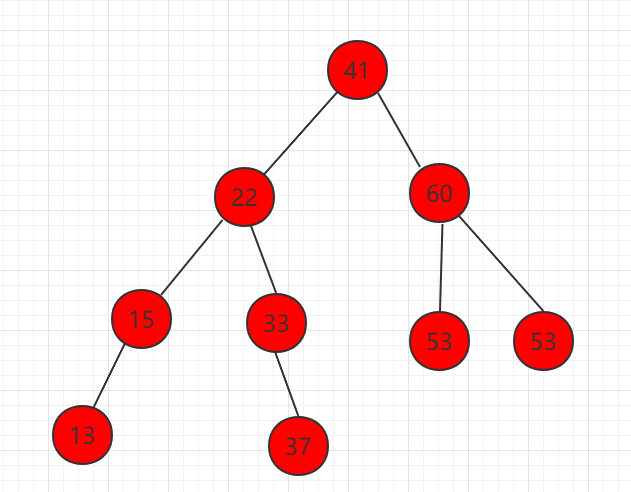
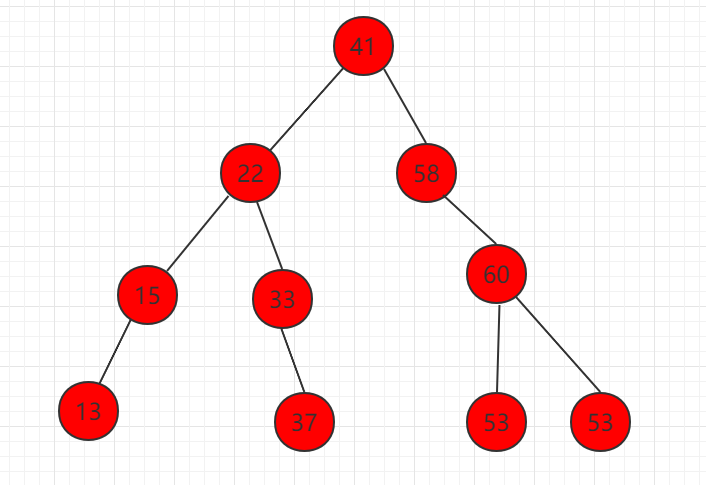
3、删除左右都有孩子的节点，如下图节点 58。

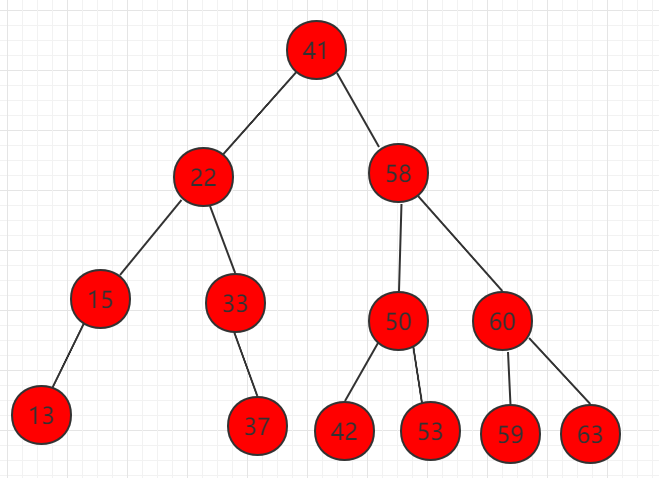
（1）找到右子树中的最小值，为节点 59

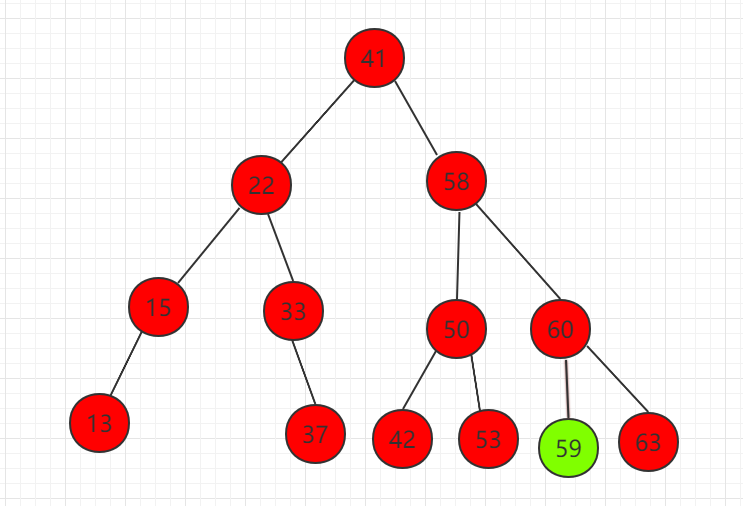
（2）节点 59 代替待删除节点 58

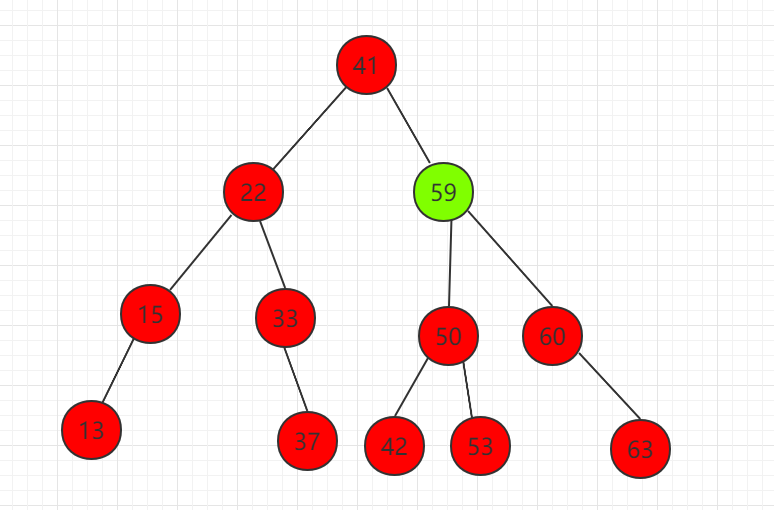
综合以上规律，删除以 node 为根的二分搜索树中键值为 key 的节点，核心代码示例：

src/demo/binary/BSTRemove.java 文件代码：
package demo.binary;

import java.util.LinkedList;

/**
 * 二分搜索树节点删除
 */
public class BSTRemove<Key extends Comparable<Key>, Value>  {
    // 树中的节点为私有的类, 外界不需要了解二分搜索树节点的具体实现
    private class Node {
        private Key key;
        private Value value;
        private Node left, right;

        public Node(Key key, Value value) {
            this.key = key;
            this.value = value;
            left = right = null;
        }

        public Node(Node node){
            this.key = node.key;
            this.value = node.value;
            this.left = node.left;
            this.right = node.right;
        }
    }

    private Node root;  // 根节点
    private int count;  // 树种的节点个数

    // 构造函数, 默认构造一棵空二分搜索树
    public BSTRemove() {
        root = null;
        count = 0;
    }

    // 返回二分搜索树的节点个数
    public int size() {
        return count;
    }

    // 返回二分搜索树是否为空
    public boolean isEmpty() {
        return count == 0;
    }

    // 向二分搜索树中插入一个新的(key, value)数据对
    public void insert(Key key, Value value){
        root = insert(root, key, value);
    }

    // 查看二分搜索树中是否存在键key
    public boolean contain(Key key){
        return contain(root, key);
    }

    // 在二分搜索树中搜索键key所对应的值。如果这个值不存在, 则返回null
    public Value search(Key key){
        return search( root , key );
    }

    // 二分搜索树的前序遍历
    public void preOrder(){
        preOrder(root);
    }

    // 二分搜索树的中序遍历
    public void inOrder(){
        inOrder(root);
    }

    // 二分搜索树的后序遍历
    public void postOrder(){
        postOrder(root);
    }

    // 二分搜索树的层序遍历
    public void levelOrder(){

        // 我们使用LinkedList来作为我们的队列
        LinkedList<Node> q = new LinkedList<Node>();
        q.add(root);
        while( !q.isEmpty() ){

            Node node = q.remove();

            System.out.println(node.key);

            if( node.left != null )
                q.add( node.left );
            if( node.right != null )
                q.add( node.right );
        }
    }

    // 寻找二分搜索树的最小的键值
    public Key minimum(){
        assert count != 0;
        Node minNode = minimum( root );
        return minNode.key;
    }

    // 寻找二分搜索树的最大的键值
    public Key maximum(){
        assert count != 0;
        Node maxNode = maximum(root);
        return maxNode.key;
    }

    // 从二分搜索树中删除最小值所在节点
    public void removeMin(){
        if( root != null )
            root = removeMin( root );
    }

    // 从二分搜索树中删除最大值所在节点
    public void removeMax(){
        if( root != null )
            root = removeMax( root );
    }

    // 从二分搜索树中删除键值为key的节点
    public void remove(Key key){
        root = remove(root, key);
    }

    //********************
    //* 二分搜索树的辅助函数
    //********************

    // 向以node为根的二分搜索树中, 插入节点(key, value), 使用递归算法
    // 返回插入新节点后的二分搜索树的根
    private Node insert(Node node, Key key, Value value){

        if( node == null ){
            count ++;
            return new Node(key, value);
        }

        if( key.compareTo(node.key) == 0 )
            node.value = value;
        else if( key.compareTo(node.key) < 0 )
            node.left = insert( node.left , key, value);
        else    // key > node->key
            node.right = insert( node.right, key, value);

        return node;
    }

    // 查看以node为根的二分搜索树中是否包含键值为key的节点, 使用递归算法
    private boolean contain(Node node, Key key){

        if( node == null )
            return false;

        if( key.compareTo(node.key) == 0 )
            return true;
        else if( key.compareTo(node.key) < 0 )
            return contain( node.left , key );
        else // key > node->key
            return contain( node.right , key );
    }

    // 在以node为根的二分搜索树中查找key所对应的value, 递归算法
    // 若value不存在, 则返回NULL
    private Value search(Node node, Key key){

        if( node == null )
            return null;

        if( key.compareTo(node.key) == 0 )
            return node.value;
        else if( key.compareTo(node.key) < 0 )
            return search( node.left , key );
        else // key > node->key
            return search( node.right, key );
    }

    // 对以node为根的二叉搜索树进行前序遍历, 递归算法
    private void preOrder(Node node){

        if( node != null ){
            System.out.println(node.key);
            preOrder(node.left);
            preOrder(node.right);
        }
    }

    // 对以node为根的二叉搜索树进行中序遍历, 递归算法
    private void inOrder(Node node){

        if( node != null ){
            inOrder(node.left);
            System.out.println(node.key);
            inOrder(node.right);
        }
    }

    // 对以node为根的二叉搜索树进行后序遍历, 递归算法
    private void postOrder(Node node){

        if( node != null ){
            postOrder(node.left);
            postOrder(node.right);
            System.out.println(node.key);
        }
    }

    // 返回以node为根的二分搜索树的最小键值所在的节点
    private Node minimum(Node node){
        if( node.left == null )
            return node;

        return minimum(node.left);
    }

    // 返回以node为根的二分搜索树的最大键值所在的节点
    private Node maximum(Node node){
        if( node.right == null )
            return node;

        return maximum(node.right);
    }

    // 删除掉以node为根的二分搜索树中的最小节点
    // 返回删除节点后新的二分搜索树的根
    private Node removeMin(Node node){

        if( node.left == null ){

            Node rightNode = node.right;
            node.right = null;
            count --;
            return rightNode;
        }

        node.left = removeMin(node.left);
        return node;
    }

    // 删除掉以node为根的二分搜索树中的最大节点
    // 返回删除节点后新的二分搜索树的根
    private Node removeMax(Node node){

        if( node.right == null ){

            Node leftNode = node.left;
            node.left = null;
            count --;
            return leftNode;
        }

        node.right = removeMax(node.right);
        return node;
    }

    // 删除掉以node为根的二分搜索树中键值为key的节点, 递归算法
    // 返回删除节点后新的二分搜索树的根
    Node remove(Node node, Key key){

        if( node == null )
            return null;

        if( key.compareTo(node.key) < 0 ){
            node.left = remove( node.left , key );
            return node;
        }
        else if( key.compareTo(node.key) > 0 ){
            node.right = remove( node.right, key );
            return node;
        }
        else{   // key == node->key

            // 待删除节点左子树为空的情况
            if( node.left == null ){
                Node rightNode = node.right;
                node.right = null;
                count --;
                return rightNode;
            }

            // 待删除节点右子树为空的情况
            if( node.right == null ){
                Node leftNode = node.left;
                node.left = null;
                count--;
                return leftNode;
            }

            // 待删除节点左右子树均不为空的情况

            // 找到比待删除节点大的最小节点, 即待删除节点右子树的最小节点
            // 用这个节点顶替待删除节点的位置
            Node successor = new Node(minimum(node.right));
            count ++;

            successor.right = removeMin(node.right);
            successor.left = node.left;

            node.left = node.right = null;
            count --;

            return successor;
        }
    }
}

二分搜索树的特性

一、顺序性
二分搜索树可以当做查找表的一种实现。

我们使用二分搜索树的目的是通过查找 key 马上得到 value。minimum、maximum、successor（后继）、predecessor（前驱）、floor（地板）、ceil（天花板、rank（排名第几的元素）、select（排名第n的元素是谁）这些都是二分搜索树顺序性的表现。

二、局限性
二分搜索树在时间性能上是具有局限性的。

如下图所示，元素节点一样，组成两种不同的二分搜索树，都是满足定义的：

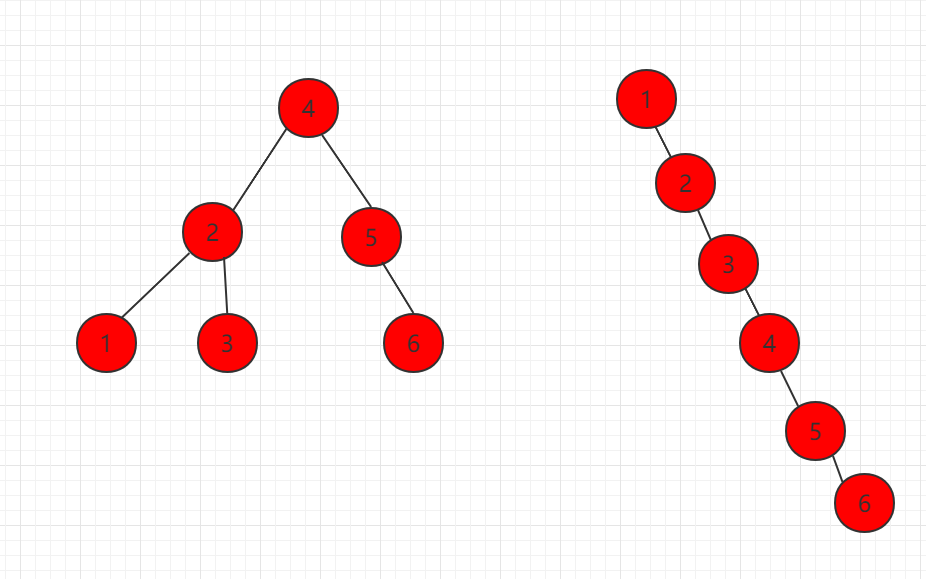
二叉搜索树可能退化成链表，相应的，二叉搜索树的查找操作是和这棵树的高度相关的，而此时这颗树的高度就是这颗树的节点数 n，同时二叉搜索树相应的算法全部退化成 O(n) 级别。

并查集

并查集基础

一、概念及其介绍
并查集是一种树型的数据结构，用于处理一些不相交集合的合并及查询问题。

并查集的思想是用一个数组表示了整片森林（parent），树的根节点唯一标识了一个集合，我们只要找到了某个元素的的树根，就能确定它在哪个集合里。

二、适用说明
并查集用在一些有 N 个元素的集合应用问题中，我们通常是在开始时让每个元素构成一个单元素的集合，然后按一定顺序将属于同一组的元素所在的集合合并，其间要反复查找一个元素在哪个集合中。这个过程看似并不复杂，但数据量极大，若用其他的数据结构来描述的话，往往在空间上过大，计算机无法承受，也无法在短时间内计算出结果，所以只能用并查集来处理。

三、并查集的基本数据表示

如上图 0-4 下面都是 0，5-9 下面都是 1，表示 0、1、2、3、4 这五个元素是相连接的，5、6、7、8、9 这五个元素是相连的。

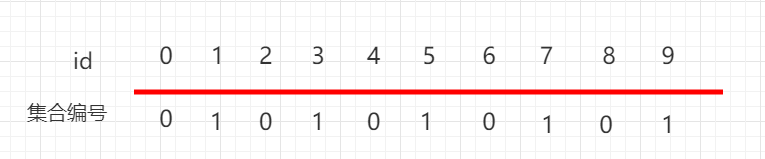
再如上图 0、2、4、6、8 下面都是 0 这个集合，表示 0、2、4、6、8 这五个元素是相连接的，1、3、5、7、9 下面都是 1 这个集合，表示 0，1、3、5、7、9 这五个元素是相连的。

构造一个类 UnionFind，初始化, 每一个id[i]指向自己, 没有合并的元素：

...
public UnionFind1(int n) {
        count = n;
        id = new int[n];
        // 初始化, 每一个id[i]指向自己, 没有合并的元素
        for (int i = 0; i < n; i++)
            id[i] = i;
    }
...

Java 实例代码

UnionFind.java 文件代码：
package demo.union;

public class UnionFind{
    private int[] id;
    // 数据个数
    private int count;

    public UnionFind1(int n) {
        count = n;
        id = new int[n];
        for (int i = 0; i < n; i++)
            id[i] = i;
    }

}  

并查集快速查找

本小节基于上一小节并查集的结构介绍基础操作，查询和合并和判断是否连接。

查询元素所在的集合编号，直接返回 id 数组值，O(1) 的时间复杂度。

...
private int find(int p) {
    assert p >= 0 && p < count;
    return id[p];
}
...

合并元素 p 和元素 q 所属的集合， 合并过程需要遍历一遍所有元素, 再将两个元素的所属集合编号合并，这个过程是 O(n) 复杂度。

...
public void unionElements(int p, int q) {
    int pID = find(p);
    int qID = find(q);
    if (pID == qID)
        return;
    for (int i = 0; i < count; i++)
        if (id[i] == pID)
            id[i] = qID;
}
...

Java 实例代码

UnionFind1.java 文件代码：
package demo.union;

/**
 * 第一版union-Find
 */
public class UnionFind1 {
    // 我们的第一版Union-Find本质就是一个数组
    private int[] id;
    // 数据个数
    private int count;

    public UnionFind1(int n) {
        count = n;
        id = new int[n];
        // 初始化, 每一个id[i]指向自己, 没有合并的元素
        for (int i = 0; i < n; i++)
            id[i] = i;
    }

    // 查找过程, 查找元素p所对应的集合编号
    private int find(int p) {
        assert p >= 0 && p < count;
        return id[p];
    }

    // 查看元素p和元素q是否所属一个集合
    // O(1)复杂度
    public boolean isConnected(int p, int q) {
        return find(p) == find(q);
    }

    // 合并元素p和元素q所属的集合
    // O(n) 复杂度
    public void unionElements(int p, int q) {

        int pID = find(p);
        int qID = find(q);

        if (pID == qID)
            return;

        // 合并过程需要遍历一遍所有元素, 将两个元素的所属集合编号合并
        for (int i = 0; i < count; i++)
            if (id[i] == pID)
                id[i] = qID;
    }
}

并查集快速合并

对于一组数据，并查集主要支持两个动作：

• union(p,q) - 将 p 和 q 两个元素连接起来。

• find§ - 查询 p 元素在哪个集合中。

• isConnected(p,q) - 查看 p 和 q 两个元素是否相连接在一起。

在上一小节中，我们用 id 数组的形式表示并查集，实际操作过程中查找的时间复杂度为 O(1)，但连接效率并不高。

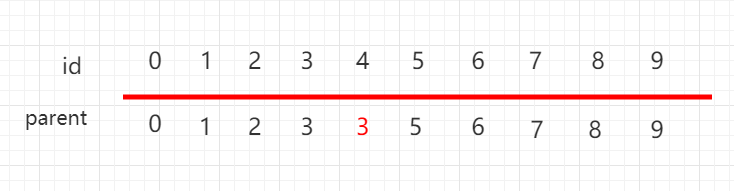
本小节，我们将用另外一种方式实现并查集。把每一个元素，看做是一个节点并且指向自己的父节点，根节点指向自己。如下图所示，节点 3 指向节点 2，代表 3 和 2 是连接在一起的，节点2本身是根节点，所以指向自己。

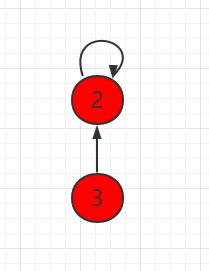
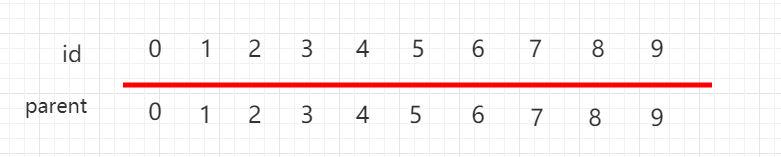
同样用数组表示并查集，但是下面一组元素用 parent 表示当前元素指向的父节点，每个元素指向自己，都是独立的。

如果此时操作 union(4,3)，将元素 4 指向元素 3：

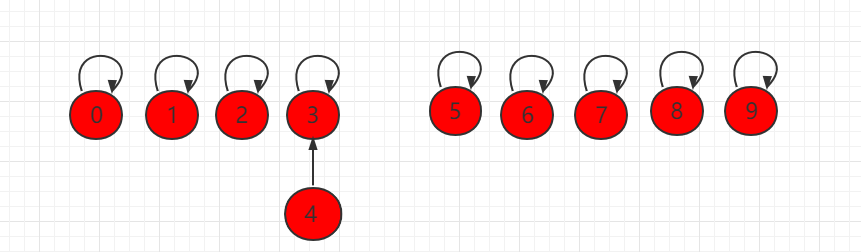
数组也进行相应改变：

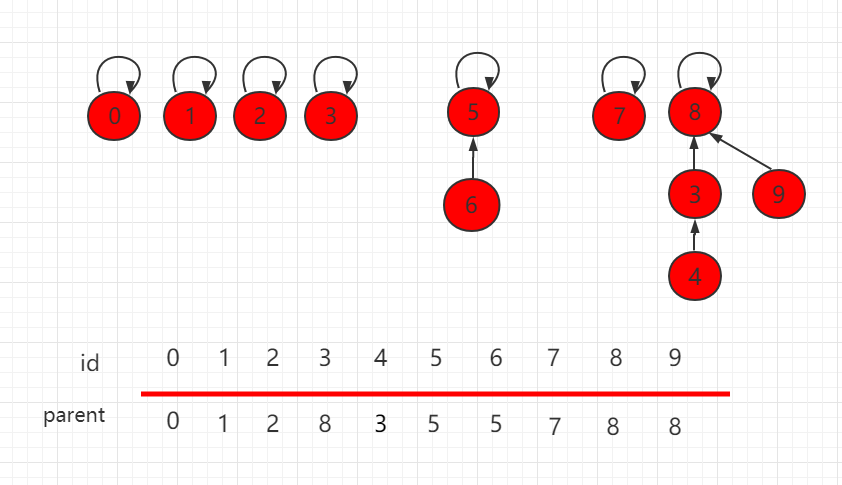
判断两个元素是否连接，只需要判断根节点是否相同即可。

如下图，节点 4 和节点 9 的根节点都是 8，所以它们是相连的。

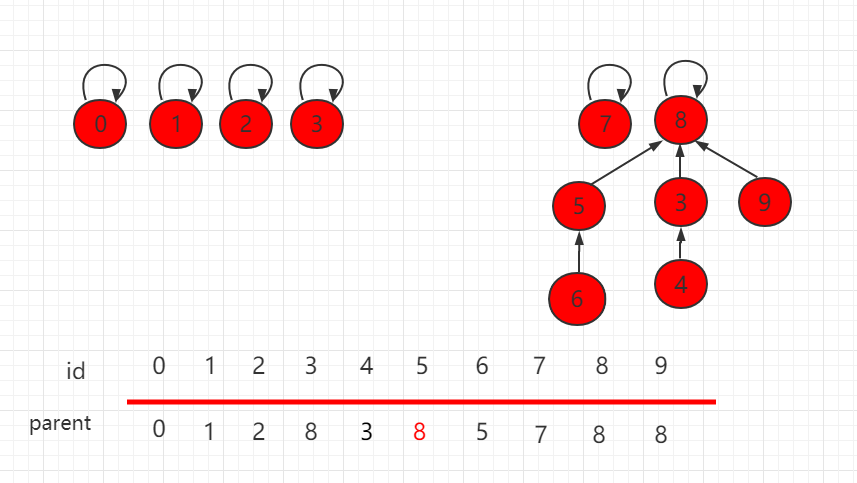
连接两个元素，只需要找到它们对应的根节点，使根节点相连，那它们就是相连的节点。

假设要使上图中的 6 和 4 相连，只需要把 6 的根节点 5 指向 4 的根节点 8 即可。

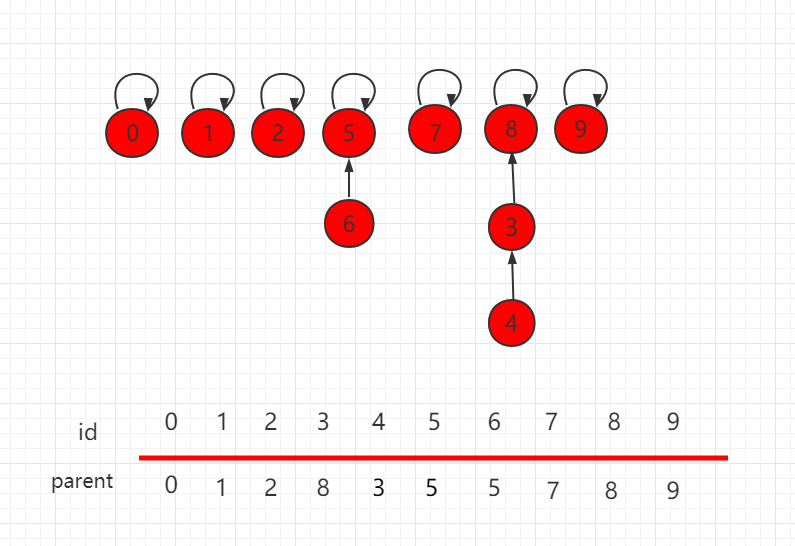
构建这种指向父节点的树形结构， 使用一个数组构建一棵指向父节点的树，parent[i] 表示 i 元素所指向的父节点。

...
private int[] parent;
private int count;  // 数据个数
...

查找过程, 查找元素 p 所对应的集合编号，不断去查询自己的父亲节点, 直到到达根节点，根节点的特点 parent[p] == p，O(h) 复杂度, h 为树的高度。

...
private int find(int p){
    assert( p >= 0 && p < count );
    while( p != parent[p] )
        p = parent[p];
    return p;
}
...

合并元素 p 和元素 q 所属的集合，分别查询两个元素的根节点，使其中一个根节点指向另外一个根节点，两个集合就合并了。这个操作是 O(h) 的时间复杂度，h 为树的高度。

public void unionElements(int p, int q){
    int pRoot = find(p);
    int qRoot = find(q);
    if( pRoot == qRoot )
        return;
    parent[pRoot] = qRoot;
}

Java 实例代码

UnionFind2.java 文件代码：
package demo.union;
/**
 * 第二版unionFind
 */
public class UnionFind2 {
    // 我们的第二版Union-Find, 使用一个数组构建一棵指向父节点的树
    // parent[i]表示第一个元素所指向的父节点
    private int[] parent;
    private int count;  // 数据个数
    // 构造函数
    public UnionFind2(int count){
        parent = new int[count];
        this.count = count;
        // 初始化, 每一个parent[i]指向自己, 表示每一个元素自己自成一个集合
        for( int i = 0 ; i < count ; i ++ )
            parent[i] = i;
    }
    // 查找过程, 查找元素p所对应的集合编号
    // O(h)复杂度, h为树的高度
    private int find(int p){
        assert( p >= 0 && p < count );
        // 不断去查询自己的父亲节点, 直到到达根节点
        // 根节点的特点: parent[p] == p
        while( p != parent[p] )
            p = parent[p];
        return p;
    }
    // 查看元素p和元素q是否所属一个集合
    // O(h)复杂度, h为树的高度
    public boolean isConnected( int p , int q ){
        return find(p) == find(q);
    }
    // 合并元素p和元素q所属的集合
    // O(h)复杂度, h为树的高度
    public void unionElements(int p, int q){
        int pRoot = find(p);
        int qRoot = find(q);
        if( pRoot == qRoot )
            return;
        parent[pRoot] = qRoot;
    }
}

并查集 size 的优化

按照上一小节的思路，我们把如下图所示的并查集，进行 union(4,9) 操作。

合并操作后的结构为：

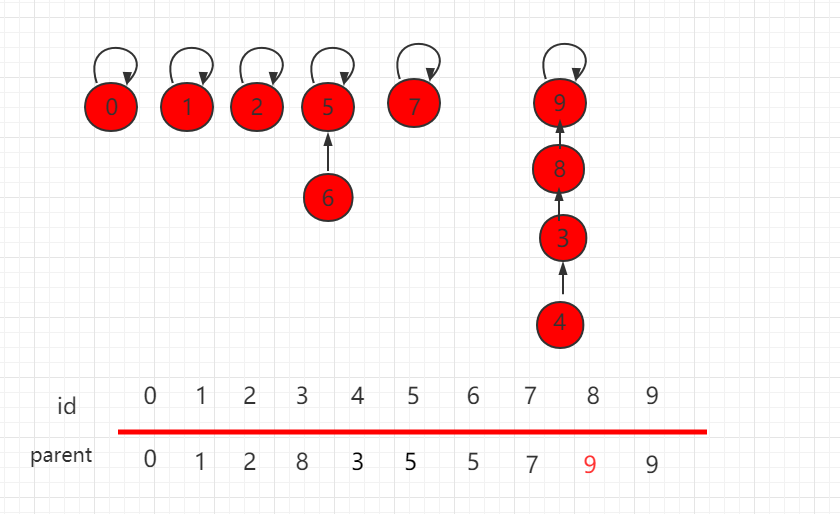
可以发现，这个结构的树的层相对较高，若此时元素数量增多，这样产生的消耗就会相对较大。解决这个问题其实很简单，在进行具体指向操作的时候先进行判断，把元素少的集合根节点指向元素多的根节点，能更高概率的生成一个层数比较低的树。

构造并查集的时候需要多一个参数，sz 数组，sz[i] 表示以 i 为根的集合中元素个数。

// 构造函数
public UnionFind3(int count){
    parent = new int[count];
    sz = new int[count];
    this.count = count;
    // 初始化, 每一个parent[i]指向自己, 表示每一个元素自己自成一个集合
    for( int i = 0 ; i < count ; i ++ ){
        parent[i] = i;
        sz[i] = 1;
    }
}

在进行合并操作时候，根据两个元素所在树的元素个数不同判断合并方向。

public void unionElements(int p, int q){
    int pRoot = find(p);
    int qRoot = find(q);
    if( pRoot == qRoot )
        return;
    if( sz[pRoot] < sz[qRoot] ){
        parent[pRoot] = qRoot;
        sz[qRoot] += sz[pRoot];
    }
    else{
        parent[qRoot] = pRoot;
        sz[pRoot] += sz[qRoot];
    }
}

优化后，合并结果如下，9 指向父节点 8。

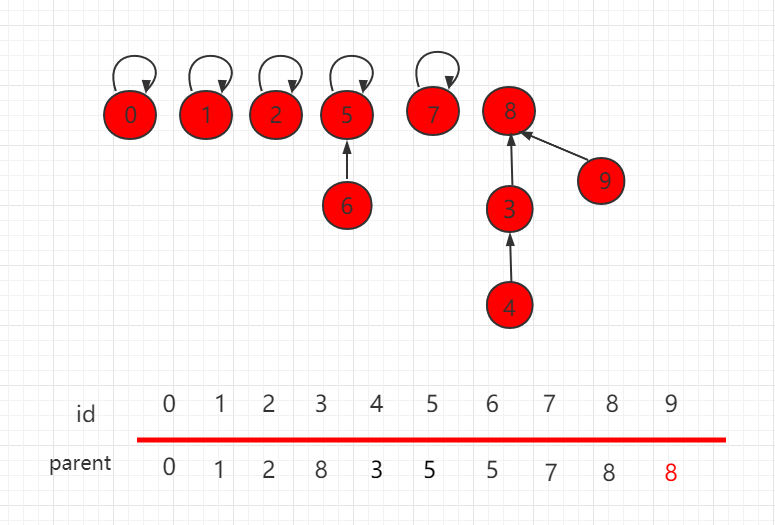
Java 实例代码

UnionFind3.java 文件代码：
package demo.union;

/**
 * 并查集size的优化
 */
public class UnionFind3 {
    // parent[i]表示第一个元素所指向的父节点
    private int[] parent;
    // sz[i]表示以i为根的集合中元素个数
    private int[] sz;
    // 数据个数
    private int count;

    // 构造函数
    public UnionFind3(int count){
        parent = new int[count];
        sz = new int[count];
        this.count = count;
        // 初始化, 每一个parent[i]指向自己, 表示每一个元素自己自成一个集合
        for( int i = 0 ; i < count ; i ++ ){
            parent[i] = i;
            sz[i] = 1;
        }
    }

    // 查找过程, 查找元素p所对应的集合编号
    // O(h)复杂度, h为树的高度
    private int find(int p){
        assert( p >= 0 && p < count );
        // 不断去查询自己的父亲节点, 直到到达根节点
        // 根节点的特点: parent[p] == p
        while( p != parent[p] )
            p = parent[p];
        return p;
    }

    // 查看元素p和元素q是否所属一个集合
    // O(h)复杂度, h为树的高度
    public boolean isConnected( int p , int q ){
        return find(p) == find(q);
    }

    // 合并元素p和元素q所属的集合
    // O(h)复杂度, h为树的高度
    public void unionElements(int p, int q){
        int pRoot = find(p);
        int qRoot = find(q);
        if( pRoot == qRoot )
            return;
        // 根据两个元素所在树的元素个数不同判断合并方向
        // 将元素个数少的集合合并到元素个数多的集合上
        if( sz[pRoot] < sz[qRoot] ){
            parent[pRoot] = qRoot;
            sz[qRoot] += sz[pRoot];
        }
        else{
            parent[qRoot] = pRoot;
            sz[pRoot] += sz[qRoot];
        }
    }
}

并查集 rank 的优化

并查集 rank 的优化
上一小节介绍了并查集基于 size 的优化，但是某些场景下，也会存在某些问题，如下图所示，操作 union(4,2)。

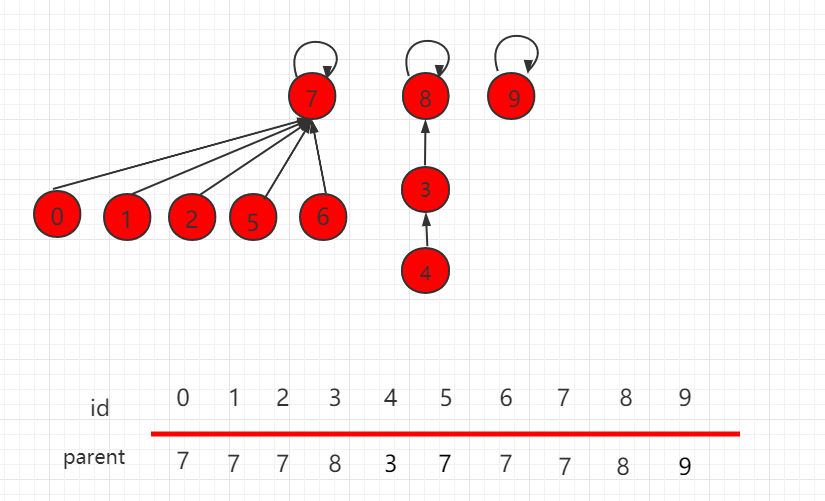
根据上一小节，size 的优化，元素少的集合根节点指向元素多的根节点。操完后，层数变为4，比之前增多了一层，如下图所示：

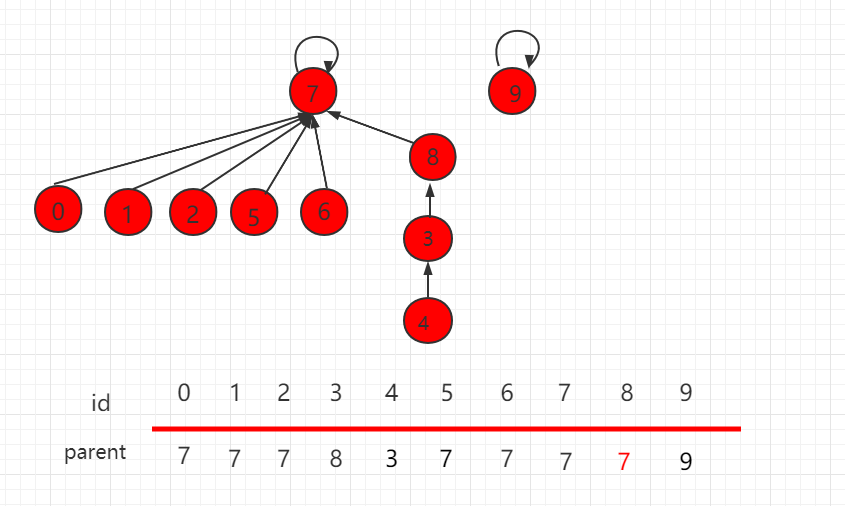
由此可知，依靠集合的 size 判断指向并不是完全正确的，更准确的是，根据两个集合层数，具体判断根节点的指向，层数少的集合根节点指向层数多的集合根节点，如下图所示，这就是基于 rank 的优化。

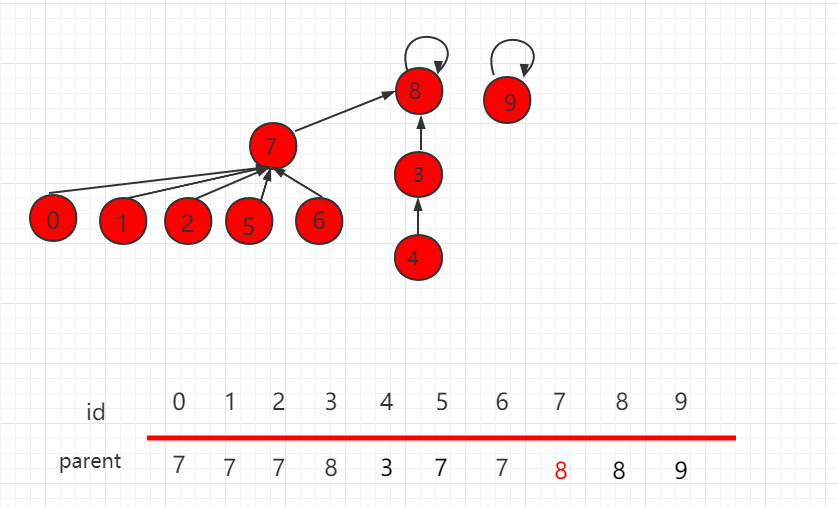
我们在并查集的属性中，添加 rank 数组，rank[i] 表示以 i 为根的集合所表示的树的层数。

...
private int[] rank;   // rank[i]表示以i为根的集合所表示的树的层数
private int[] parent; // parent[i]表示第i个元素所指向的父节点
private int count;    // 数据个数
...

构造函数相应作出修改：

...
// 构造函数
public UnionFind4(int count){
    rank = new int[count];
    parent = new int[count];
    this.count = count;
    // 初始化, 每一个parent[i]指向自己, 表示每一个元素自己自成一个集合
    for( int i = 0 ; i < count ; i ++ ){
        parent[i] = i;
        rank[i] = 1;
    }
}
...

合并两元素的时候，需要比较根节点集合的层数，整个过程是 O(h)复杂度，h为树的高度。

...
public void unionElements(int p, int q){
    int pRoot = find(p);
    int qRoot = find(q);
    if( pRoot == qRoot )
        return;

    if( rank[pRoot] < rank[qRoot] ){
        parent[pRoot] = qRoot;
    }
    else if( rank[qRoot] < rank[pRoot]){
        parent[qRoot] = pRoot;
    }
    else{ // rank[pRoot] == rank[qRoot]
        parent[pRoot] = qRoot;
        rank[qRoot] += 1;   // 此时, 我维护rank的值
    }
}
...

Java 实例代码

UnionFind3.java 文件代码：
package demo.union;
/**
 * 基于rank的优化
 */
public class UnionFind4 {
    private int[] rank;   // rank[i]表示以i为根的集合所表示的树的层数
    private int[] parent; // parent[i]表示第i个元素所指向的父节点
    private int count;    // 数据个数
    // 构造函数
    public UnionFind4(int count){
        rank = new int[count];
        parent = new int[count];
        this.count = count;
        // 初始化, 每一个parent[i]指向自己, 表示每一个元素自己自成一个集合
        for( int i = 0 ; i < count ; i ++ ){
            parent[i] = i;
            rank[i] = 1;
        }
    }
    // 查找过程, 查找元素p所对应的集合编号
    // O(h)复杂度, h为树的高度
    private int find(int p){
        assert( p >= 0 && p < count );
        // 不断去查询自己的父亲节点, 直到到达根节点
        // 根节点的特点: parent[p] == p
        while( p != parent[p] )
            p = parent[p];
        return p;
    }
    // 查看元素p和元素q是否所属一个集合
    // O(h)复杂度, h为树的高度
    public boolean isConnected( int p , int q ){
        return find(p) == find(q);
    }
    // 合并元素p和元素q所属的集合
    // O(h)复杂度, h为树的高度
    public void unionElements(int p, int q){
        int pRoot = find(p);
        int qRoot = find(q);
        if( pRoot == qRoot )
            return;
        if( rank[pRoot] < rank[qRoot] ){
            parent[pRoot] = qRoot;
        }
        else if( rank[qRoot] < rank[pRoot]){
            parent[qRoot] = pRoot;
        }
        else{ // rank[pRoot] == rank[qRoot]
            parent[pRoot] = qRoot;
            rank[qRoot] += 1;   // 维护rank的值
        }
    }
}

并查集路径压缩

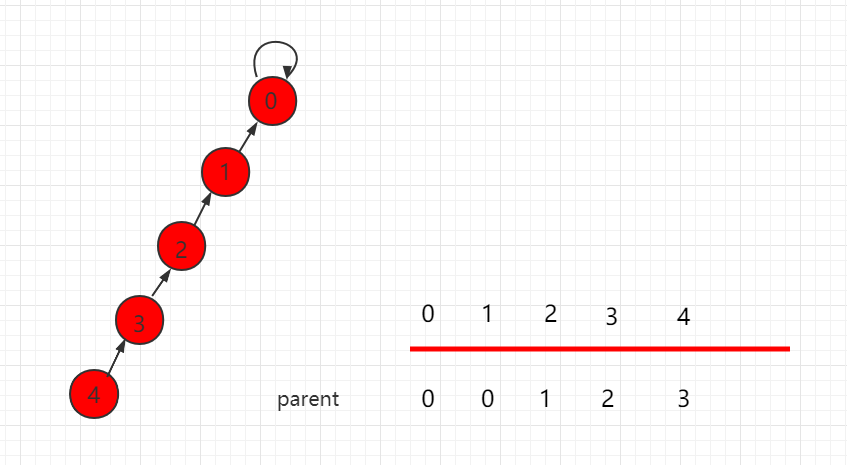
并查集里的 find 函数里可以进行路径压缩，是为了更快速的查找一个点的根节点。对于一个集合树来说，它的根节点下面可以依附着许多的节点，因此，我们可以尝试在 find 的过程中，从底向上，如果此时访问的节点不是根节点的话，那么我们可以把这个节点尽量的往上挪一挪，减少数的层数，这个过程就叫做路径压缩。

如下图中，find(4) 的过程就可以路径压缩，让数的层数更少。

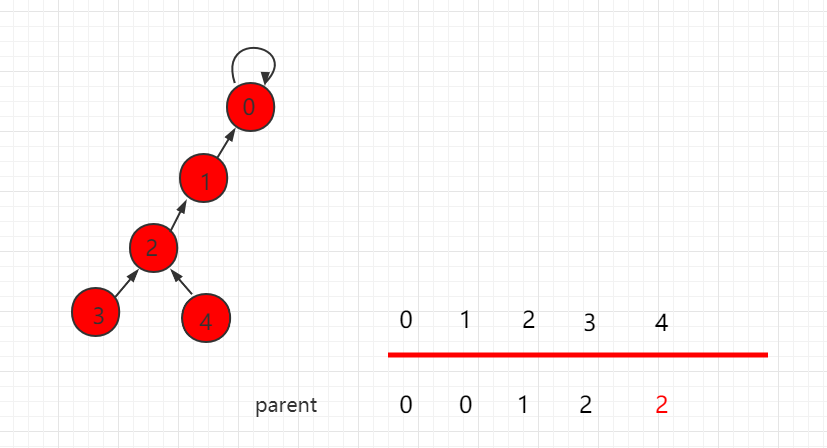
节点 4 往上寻找根节点时，压缩第一步，树的层数就减少了一层：

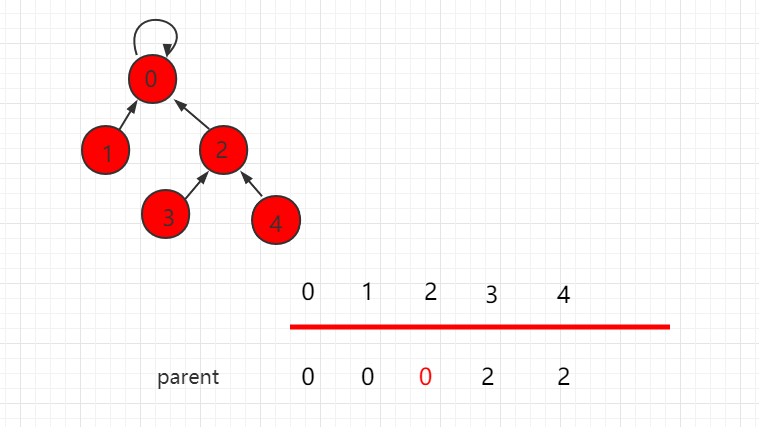
节点 2 向上寻找，也不是根节点，那么把元素 2 指向原来父节点的父节点，操后后树的层数相应减少了一层，同时返回根节点 0。

find 过程代码修改为 ：

// 查找过程, 查找元素p所对应的集合编号
// O(h)复杂度, h为树的高度
private int find(int p){
    assert( p >= 0 && p < count );

    // path compression 1
    while( p != parent[p] ){
        parent[p] = parent[parent[p]];
        p = parent[p];
    }
    return p;

}

上述路径压缩并不是最优的方式，我们可以把最初的树压缩成下图所示，层数是最少的。

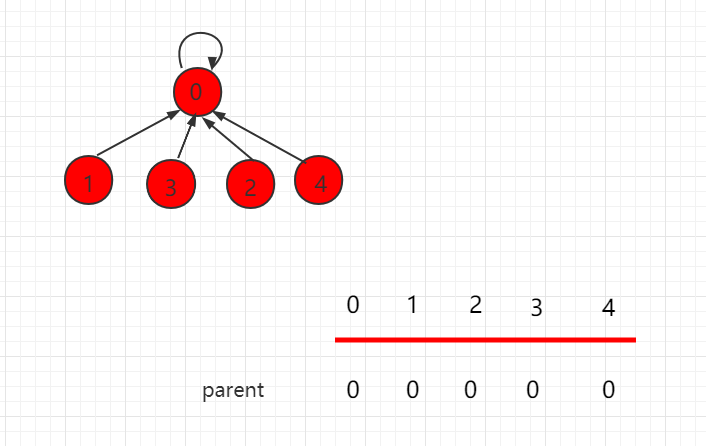
这个 find 过程代表表示为:

...
// 查找过程, 查找元素p所对应的集合编号
// O(h)复杂度, h为树的高度
private int find(int p) {
    assert (p >= 0 && p < count);

    //第二种路径压缩算法
    if (p != parent[p])
        parent[p] = find(parent[p]);
    return parent[p];
}
...

Java 实例代码

UnionFind3.java 文件代码：
package demo.union;

/**
 * 基于rank的优化
 */
public class UnionFind4 {

    private int[] rank;   // rank[i]表示以i为根的集合所表示的树的层数
    private int[] parent; // parent[i]表示第i个元素所指向的父节点
    private int count;    // 数据个数

    // 构造函数
    public UnionFind4(int count){
        rank = new int[count];
        parent = new int[count];
        this.count = count;
        // 初始化, 每一个parent[i]指向自己, 表示每一个元素自己自成一个集合
        for( int i = 0 ; i < count ; i ++ ){
            parent[i] = i;
            rank[i] = 1;
        }
    }

    // 查找过程, 查找元素p所对应的集合编号
    // O(h)复杂度, h为树的高度
    private int find(int p){
        assert( p >= 0 && p < count );
        // 不断去查询自己的父亲节点, 直到到达根节点
        // 根节点的特点: parent[p] == p
        while( p != parent[p] )
            p = parent[p];
        return p;

        //第二种路径压缩算法
        //if( p != parent[p] )
        //parent[p] = find( parent[p] );
        //return parent[p];
    }

    // 查看元素p和元素q是否所属一个集合
    // O(h)复杂度, h为树的高度
    public boolean isConnected( int p , int q ){
        return find(p) == find(q);
    }

    // 合并元素p和元素q所属的集合
    // O(h)复杂度, h为树的高度
    public void unionElements(int p, int q){

        int pRoot = find(p);
        int qRoot = find(q);

        if( pRoot == qRoot )
            return;

        if( rank[pRoot] < rank[qRoot] ){
            parent[pRoot] = qRoot;
        }
        else if( rank[qRoot] < rank[pRoot]){
            parent[qRoot] = pRoot;
        }
        else{ // rank[pRoot] == rank[qRoot]
            parent[pRoot] = qRoot;
            rank[qRoot] += 1;   // 维护rank的值
        }
    }
}

图论

图论基础和表示

一、概念及其介绍
图论(Graph Theory)是离散数学的一个分支，是一门研究图(Graph)的学问。

图是用来对对象之间的成对关系建模的数学结构，由"节点"或"顶点"(Vertex）以及连接这些顶点的"边"（Edge）组成。

值得注意的是，图的顶点集合不能为空，但边的集合可以为空。图可能是无向的，这意味着图中的边在连接顶点时无需区分方向。否则，称图是有向的。下面左图是一个典型的无向图结构，右图则属于有向图。本章节介绍的图都是无向图。

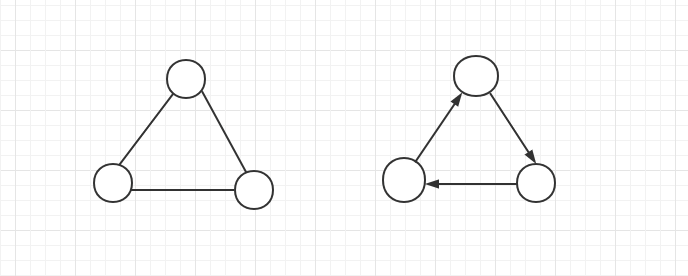
图的分类：无权图和有权图，连接节点与节点的边是否有数值与之对应，有的话就是有权图，否则就是无权图。

图的连通性：在图论中，连通图基于连通的概念。在一个无向图 G 中，若从顶点 i 到顶点 j 有路径相连（当然从j到i也一定有路径），则称 i 和 j 是连通的。如果 G 是有向图，那么连接i和j的路径中所有的边都必须同向。如果图中任意两点都是连通的，那么图被称作连通图。如果此图是有向图，则称为强连通图（注意：需要双向都有路径）。图的连通性是图的基本性质。

完全图：完全是一个简单的无向图，其中每对不同的顶点之间都恰连有一条边相连。

自环边：一条边的起点终点是一个点。

平行边：两个顶点之间存在多条边相连接。

二、适用说明
图可用于在物理、生物、社会和信息系统中建模许多类型的关系和过程，许多实际问题可以用图来表示。因此，图论成为运筹学、控制论、信息论、网络理论、博弈论、物理学、化学、生物学、社会科学、语言学、计算机科学等众多学科强有力的数学工具。在强调其应用于现实世界的系统时，网络有时被定义为一个图，其中属性(例如名称)之间的关系以节点和或边的形式关联起来。

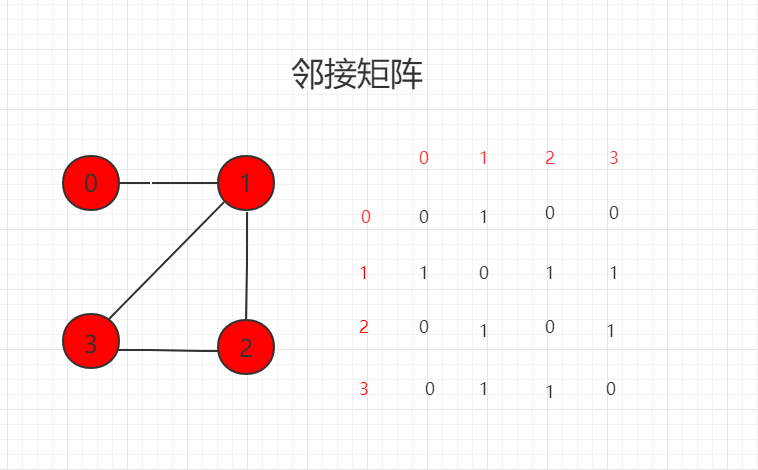
三、图的表达形式
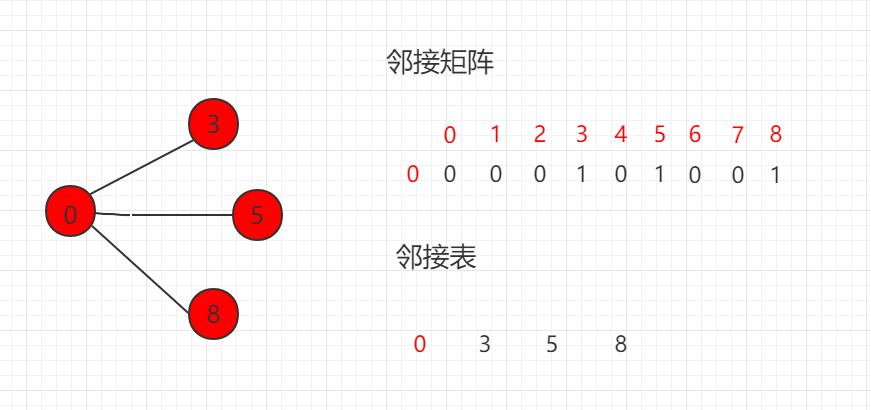
邻接矩阵：1 表示相连接，0 表示不相连。

邻接表：只表达和顶点相连接的顶点信息

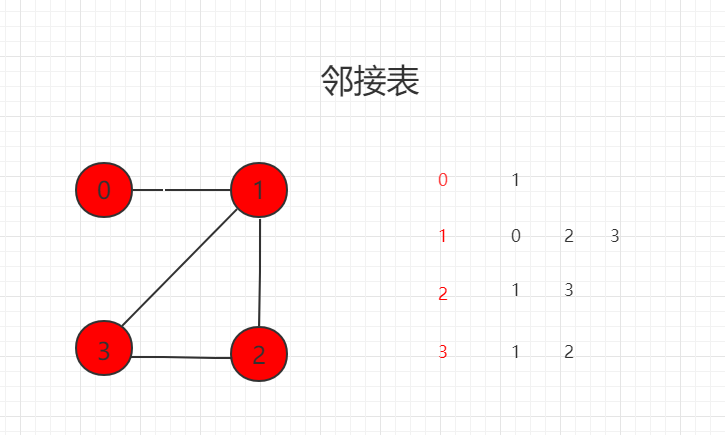
邻接表适合表示稀疏图 (Sparse Graph)

邻接矩阵适合表示稠密图 (Dense Graph)

Java 实例代码

(1) 邻接矩阵

src/demo/graph/DenseGraph.java 文件代码：
package demo.graph;

/**
 * 邻接矩阵
 */
public class DenseGraph {
    // 节点数
    private int n;
    // 边数
    private int m;
    // 是否为有向图
    private boolean directed;
    // 图的具体数据
    private boolean[][] g;

    // 构造函数
    public DenseGraph( int n , boolean directed ){
        assert n >= 0;
        this.n = n;
        this.m = 0;
        this.directed = directed;
        // g初始化为n*n的布尔矩阵, 每一个g[i][j]均为false, 表示没有任和边
        // false为boolean型变量的默认值
        g = new boolean[n][n];
    }
    // 返回节点个数
    public int V(){ return n;}
    // 返回边的个数
    public int E(){ return m;}

    // 向图中添加一个边
    public void addEdge( int v , int w ){
        assert v >= 0 && v < n ;
        assert w >= 0 && w < n ;
        if( hasEdge( v , w ) )
            return;
        g[v][w] = true;
        if( !directed )
            g[w][v] = true;
        m ++;
    }

    // 验证图中是否有从v到w的边
    boolean hasEdge( int v , int w ){
        assert v >= 0 && v < n ;
        assert w >= 0 && w < n ;
        return g[v][w];
    }
}

（2）邻接表

src/demo/graph/SparseGraph.java 文件代码：
package demo.graph;

import java.util.Vector;

/**
 * 邻接表
 */
public class SparseGraph {
    // 节点数
    private int n;
    // 边数
    private int m;
    // 是否为有向图
    private boolean directed;
    // 图的具体数据
    private Vector<Integer>[] g;

    // 构造函数
    public SparseGraph( int n , boolean directed ){
        assert n >= 0;
        this.n = n;
        this.m = 0;  
        this.directed = directed;
        // g初始化为n个空的vector, 表示每一个g[i]都为空, 即没有任和边
        g = (Vector<Integer>[])new Vector[n];
        for(int i = 0 ; i < n ; i ++)
            g[i] = new Vector<Integer>();
    }
    // 返回节点个数
    public int V(){ return n;}
    // 返回边的个数
    public int E(){ return m;}
    // 向图中添加一个边
    public void addEdge( int v, int w ){
        assert v >= 0 && v < n ;
        assert w >= 0 && w < n ;
        g[v].add(w);
        if( v != w && !directed )
            g[w].add(v);
        m ++;
    }

    // 验证图中是否有从v到w的边
    boolean hasEdge( int v , int w ){

        assert v >= 0 && v < n ;
        assert w >= 0 && w < n ;

        for( int i = 0 ; i < g[v].size() ; i ++ )
            if( g[v].elementAt(i) == w )
                return true;
        return false;
    }
}

相邻节点迭代器

图论中最常见的操作就是遍历邻边，通过一个顶点遍历相关的邻边。邻接矩阵的遍历邻边的时间复杂度为 O(V)，邻接表可以直接找到，效率更高。

邻接矩阵迭代:

...
public Iterable<Integer> adj(int v) {
    assert v >= 0 && v < n;
    Vector<Integer> adjV = new Vector<Integer>();
    for(int i = 0 ; i < n ; i ++ )
        if( g[v][i] )
            adjV.add(i);
    return adjV;
}
...

邻接表迭代：

...
// 返回图中一个顶点的所有邻边
// 由于java使用引用机制，返回一个Vector不会带来额外开销,
public Iterable<Integer> adj(int v) {
    assert v >= 0 && v < n;
    return g[v];
}
...

对于这两种图的表达方式我们可以抽象出一个接口，生成这一套算法的框架，而不用去考虑底层是邻接表还是邻接矩阵。

本小节写了一个测试用例 GraphReadTest，通过调用抽象接口实现图的展示，可以在 read 包查看。

/**
 * 图的抽象接口
 */
public interface Graph {
    public int V();
    public int E();
    public void addEdge( int v , int w );
    boolean hasEdge( int v , int w );
    void show();
    public Iterable<Integer> adj(int v);
}

Java 实例代码

（1）邻接矩阵迭代

src/demo/graph/DenseGraphIterater.java 文件代码：
package demo.graph;

import java.util.Vector;

/**
 * 邻接矩阵迭代
 */
public class DenseGraphIterater {
    // 节点数
    private int n;
    // 边数
    private int m;
    // 是否为有向图
    private boolean directed;
    // 图的具体数据
    private boolean[][] g;

    // 构造函数
    public DenseGraphIterater( int n , boolean directed ){
        assert n >= 0;
        this.n = n;
        this.m = 0;
        this.directed = directed;
        // g初始化为n*n的布尔矩阵, 每一个g[i][j]均为false, 表示没有任和边
        // false为boolean型变量的默认值
        g = new boolean[n][n];
    }
    // 返回节点个数
    public int V(){ return n;}
    // 返回边的个数
    public int E(){ return m;}

    // 向图中添加一个边
    public void addEdge( int v , int w ){
        assert v >= 0 && v < n ;
        assert w >= 0 && w < n ;
        if( hasEdge( v , w ) )
            return;
        g[v][w] = true;
        if( !directed )
            g[w][v] = true;
        m ++;
    }

    // 验证图中是否有从v到w的边
    boolean hasEdge( int v , int w ){
        assert v >= 0 && v < n ;
        assert w >= 0 && w < n ;
        return g[v][w];
    }
    // 返回图中一个顶点的所有邻边
    // 由于java使用引用机制，返回一个Vector不会带来额外开销,
    public Iterable<Integer> adj(int v) {
        assert v >= 0 && v < n;
        Vector<Integer> adjV = new Vector<Integer>();
        for(int i = 0 ; i < n ; i ++ )
            if( g[v][i] )
                adjV.add(i);
        return adjV;
    }
}

（2）邻接表迭代

src/demo/graph/SparseGraphIterater.java 文件代码：
package demo.graph;

import java.util.Vector;

/**
 * 邻接表迭代
 */
public class SparseGraphIterater {

    private int n;  // 节点数
    private int m;  // 边数
    private boolean directed;    // 是否为有向图
    private Vector<Integer>[] g; // 图的具体数据

    // 构造函数
    public SparseGraphIterater( int n , boolean directed ){
        assert n >= 0;
        this.n = n;
        this.m = 0;    // 初始化没有任何边
        this.directed = directed;
        // g初始化为n个空的vector, 表示每一个g[i]都为空, 即没有任和边
        g = (Vector<Integer>[])new Vector[n];
        for(int i = 0 ; i < n ; i ++)
            g[i] = new Vector<Integer>();
    }
    public int V(){ return n;} // 返回节点个数
    public int E(){ return m;} // 返回边的个数

    // 向图中添加一个边
    public void addEdge( int v, int w ){

        assert v >= 0 && v < n ;
        assert w >= 0 && w < n ;

        g[v].add(w);
        if( v != w && !directed )
            g[w].add(v);

        m ++;
    }

    // 验证图中是否有从v到w的边
    boolean hasEdge( int v , int w ){

        assert v >= 0 && v < n ;
        assert w >= 0 && w < n ;

        for( int i = 0 ; i < g[v].size() ; i ++ )
            if( g[v].elementAt(i) == w )
                return true;
        return false;
    }

    // 返回图中一个顶点的所有邻边
    // 由于java使用引用机制，返回一个Vector不会带来额外开销,
    public Iterable<Integer> adj(int v) {
        assert v >= 0 && v < n;
        return g[v];
    }
}

深度优先遍历与连通分量

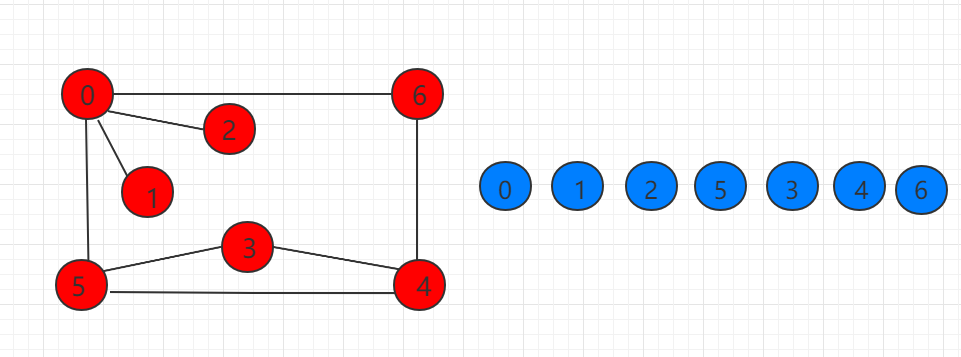
深度优先遍历(Depth First Search)的主要思想是首先以一个未被访问过的顶点作为起始顶点，沿当前顶点的边走到未访问过的顶点。当没有未访问过的顶点时，则回到上一个顶点，继续试探别的顶点，直至所有的顶点都被访问过。

下图示例的图从 0 开始遍历顺序如右图所示：

无向图 G 的一个极大连通子图称为 G 的一个连通分量（或连通分支）。连通图只有一个连通分量，即其自身；非连通的无向图有多个连通分量。连通分量与连通分量之间没有任何边相连。深度优先遍历可以用来求连通分量。

下面以求连通分量为例，来实现图的深度优先遍历，称为 dfs。下面代码片段中，visited 数组记录 dfs 的过程中节点是否被访问，ccount 记录联通分量个数，id 数组代表每个节点所对应的联通分量标记，两个节点拥有相同的 id 值代表属于同一联通分量。

...
// 构造函数, 求出无权图的联通分量
public Components(Graph graph){
    // 算法初始化
    G = graph;
    visited = new boolean[G.V()];
    id = new int[G.V()];
    ccount = 0;
    for( int i = 0 ; i < G.V() ; i ++ ){
        visited[i] = false;
        id[i] = -1;
    }
    // 求图的联通分量
    for( int i = 0 ; i < G.V() ; i ++ )
        if( !visited[i] ){
            dfs(i);
            ccount ++;
        }
}
...

图的深度优先遍历是个递归过程，实现代码：

...
// 图的深度优先遍历
void dfs( int v ){

    visited[v] = true;
    id[v] = ccount;

    for( int i: G.adj(v) ){
        if( !visited[i] )
            dfs(i);
    }
}
...

Java 实例代码

src/demo/graph/Components.java 文件代码：
package demo.graph;

import demo.graph.read.Graph;

/**
 * 深度优先遍历
 */
public class Components {

    Graph G;                    // 图的引用
    private boolean[] visited;  // 记录dfs的过程中节点是否被访问
    private int ccount;         // 记录联通分量个数
    private int[] id;           // 每个节点所对应的联通分量标记

    // 图的深度优先遍历
    void dfs( int v ){

        visited[v] = true;
        id[v] = ccount;

        for( int i: G.adj(v) ){
            if( !visited[i] )
                dfs(i);
        }
    }

    // 构造函数, 求出无权图的联通分量
    public Components(Graph graph){

        // 算法初始化
        G = graph;
        visited = new boolean[G.V()];
        id = new int[G.V()];
        ccount = 0;
        for( int i = 0 ; i < G.V() ; i ++ ){
            visited[i] = false;
            id[i] = -1;
        }

        // 求图的联通分量
        for( int i = 0 ; i < G.V() ; i ++ )
            if( !visited[i] ){
                dfs(i);
                ccount ++;
            }
    }

    // 返回图的联通分量个数
    int count(){
        return ccount;
    }

    // 查询点v和点w是否联通
    boolean isConnected( int v , int w ){
        assert v >= 0 && v < G.V();
        assert w >= 0 && w < G.V();
        return id[v] == id[w];
    }
}

寻路算法

图的寻路算法也可以通过深度优先遍历 dfs 实现，寻找图 graph 从起始 s 点到其他点的路径，在上一小节的实现类中添加全局变量 from数组记录路径，from[i] 表示查找的路径上i的上一个节点。

首先构造函数初始化寻路算法的初始条件，from = new int[G.V()] 和 from = new int[G.V()]，并在循环中设置默认值，visited 数组全部为false，from 数组全部为 -1 值，后面对起始节点进行 dfs 的递归处理。

...
// 构造函数, 寻路算法, 寻找图graph从s点到其他点的路径
public Path(Graph graph, int s){
    // 算法初始化
    G = graph;
    assert s >= 0 && s < G.V();
    visited = new boolean[G.V()];
    from = new int[G.V()];
    for( int i = 0 ; i < G.V() ; i ++ ){
        visited[i] = false;
        from[i] = -1;
    }
    this.s = s;
    // 寻路算法
    dfs(s);
}
...

那么判断 s 点到 w 点是否有路径，只要查询 visited 对应数组值即可。

...
boolean hasPath(int w){
    assert w >= 0 && w < G.V();
    return visited[w];
}
...

获取 s 点到 w 点的具体路径，我们用 path 方法来实现，先判断是否连通，可调用 hasPath 方法，由构造函数可知只需通过 from 数组往上追溯就能找到所有的路径。

...
Vector<Integer> path(int w){
    assert hasPath(w) ;
    Stack<Integer> s = new Stack<Integer>();
    // 通过from数组逆向查找到从s到w的路径, 存放到栈中
    int p = w;
    while( p != -1 ){
        s.push(p);
        p = from[p];
    }
    // 从栈中依次取出元素, 获得顺序的从s到w的路径
    Vector<Integer> res = new Vector<Integer>();
    while( !s.empty() )
        res.add( s.pop() );
    return res;
}
...

Java 实例代码

src/demo/graph/Path.java 文件代码：
package demo.graph;

import demo.graph.read.Graph;

import java.util.Stack;
import java.util.Vector;

/**
 * 寻路
 */
public class Path {
    // 图的引用
    private Graph G;
    // 起始点
    private int s;
    // 记录dfs的过程中节点是否被访问
    private boolean[] visited;
    // 记录路径, from[i]表示查找的路径上i的上一个节点
    private int[] from;

    // 图的深度优先遍历
    private void dfs( int v ){
        visited[v] = true;
        for( int i : G.adj(v) )
            if( !visited[i] ){
                from[i] = v;
                dfs(i);
            }
    }

    // 构造函数, 寻路算法, 寻找图graph从s点到其他点的路径
    public Path(Graph graph, int s){
        // 算法初始化
        G = graph;
        assert s >= 0 && s < G.V();
        visited = new boolean[G.V()];
        from = new int[G.V()];
        for( int i = 0 ; i < G.V() ; i ++ ){
            visited[i] = false;
            from[i] = -1;
        }
        this.s = s;
        // 寻路算法
        dfs(s);
    }

    // 查询从s点到w点是否有路径
    boolean hasPath(int w){
        assert w >= 0 && w < G.V();
        return visited[w];
    }

    // 查询从s点到w点的路径, 存放在vec中
    Vector<Integer> path(int w){

        assert hasPath(w) ;

        Stack<Integer> s = new Stack<Integer>();
        // 通过from数组逆向查找到从s到w的路径, 存放到栈中
        int p = w;
        while( p != -1 ){
            s.push(p);
            p = from[p];
        }

        // 从栈中依次取出元素, 获得顺序的从s到w的路径
        Vector<Integer> res = new Vector<Integer>();
        while( !s.empty() )
            res.add( s.pop() );

        return res;
    }

    // 打印出从s点到w点的路径
    void showPath(int w){

        assert hasPath(w) ;

        Vector<Integer> vec = path(w);
        for( int i = 0 ; i < vec.size() ; i ++ ){
            System.out.print(vec.elementAt(i));
            if( i == vec.size() - 1 )
                System.out.println();
            else
                System.out.print(" -> ");
        }
    }
}

广度优先遍历与最短路径

广度优先遍历从某个顶点 v 出发，首先访问这个结点，并将其标记为已访问过，然后顺序访问结点v的所有未被访问的邻接点 {vi,…,vj} ，并将其标记为已访问过，然后将 {vi,…,vj} 中的每一个节点重复节点v的访问方法，直到所有结点都被访问完为止。

我们可以分为三个步骤：

（1）使用一个辅助队列 q，首先将顶点 v 入队，将其标记为已访问，然后循环检测队列是否为空。
（2）如果队列不为空，则取出队列第一个元素，并将与该元素相关联的所有未被访问的节点入队，将这些节点标记为已访问。
（3）如果队列为空，则说明已经按照广度优先遍历了所有的节点。
下图所示，右边蓝色表示从 0 开始遍历节点的顺序，下面是记录距离 0 的距离，可知广度优先遍历能求出无权图的最短路径。

下面用代码展示如何用广度优先遍历方式完成遍历，并且查询到最短路径。我们在上一小节代码的基础上增加一全局变量 ord 数组，记录路径中节点的次序。ord[i] 表示 i 节点在路径中的次序。同时构造函数做出相应调整，在遍历相邻节点时 每访问一个未被访问的节点进行 ord[i] = ord[v] + 1记录距离。邻接表的广度优先遍历时间复杂度为 O(V+E)，邻接矩阵的时间复杂度为O(V^2)。

...
// 构造函数, 寻路算法, 寻找图graph从s点到其他点的路径
public ShortestPath(Graph graph, int s){
    // 算法初始化
    G = graph;
    assert s >= 0 && s < G.V();

    visited = new boolean[G.V()];
    from = new int[G.V()];
    ord = new int[G.V()];
    for( int i = 0 ; i < G.V() ; i ++ ){
        visited[i] = false;
        from[i] = -1;
        ord[i] = -1;
    }
    this.s = s;
    // 无向图最短路径算法, 从s开始广度优先遍历整张图
    LinkedList<Integer> q = new LinkedList<Integer>();
    q.push( s );
    visited[s] = true;
    ord[s] = 0;
    while( !q.isEmpty() ){
        int v = q.pop();
        for( int i : G.adj(v) )
            if( !visited[i] ){
                q.push(i);
                visited[i] = true;
                from[i] = v;
                ord[i] = ord[v] + 1;
            }
    }
}
...

查看从 s 点到 w 点的最短路径长度，若从 s 到 w 不可达，返回-1。

...
public int length(int w){
    assert w >= 0 && w < G.V();
    return ord[w];
}
...
Java 实例代码
源码包下载：Download

src/demo/graph/ShortestPath.java 文件代码：
package demo.graph;

import demo.graph.read.Graph;

import java.util.LinkedList;
import java.util.Stack;
import java.util.Vector;

/**
 * 广度优先遍历与最短路径
 */
public class ShortestPath {
    // 图的引用
    private Graph G;
    // 起始点
    private int s;
    // 记录dfs的过程中节点是否被访问
    private boolean[] visited;
    // 记录路径, from[i]表示查找的路径上i的上一个节点
    private int[] from;
    // 记录路径中节点的次序。ord[i]表示i节点在路径中的次序。
    private int[] ord;
    // 构造函数, 寻路算法, 寻找图graph从s点到其他点的路径
    public ShortestPath(Graph graph, int s){

        // 算法初始化
        G = graph;
        assert s >= 0 && s < G.V();

        visited = new boolean[G.V()];
        from = new int[G.V()];
        ord = new int[G.V()];
        for( int i = 0 ; i < G.V() ; i ++ ){
            visited[i] = false;
            from[i] = -1;
            ord[i] = -1;
        }
        this.s = s;
        // 无向图最短路径算法, 从s开始广度优先遍历整张图
        LinkedList<Integer> q = new LinkedList<Integer>();
        q.push( s );
        visited[s] = true;
        ord[s] = 0;
        while( !q.isEmpty() ){
            int v = q.pop();
            for( int i : G.adj(v) )
                if( !visited[i] ){
                    q.push(i);
                    visited[i] = true;
                    from[i] = v;
                    ord[i] = ord[v] + 1;
                }
        }
    }

    // 查询从s点到w点是否有路径
    public boolean hasPath(int w){
        assert w >= 0 && w < G.V();
        return visited[w];
    }
    // 查询从s点到w点的路径, 存放在vec中
    public Vector<Integer> path(int w){
        assert hasPath(w) ;
        Stack<Integer> s = new Stack<Integer>();
        // 通过from数组逆向查找到从s到w的路径, 存放到栈中
        int p = w;
        while( p != -1 ){
            s.push(p);
            p = from[p];
        }

        // 从栈中依次取出元素, 获得顺序的从s到w的路径
        Vector<Integer> res = new Vector<Integer>();
        while( !s.empty() )
            res.add( s.pop() );

        return res;
    }

    // 打印出从s点到w点的路径
    public void showPath(int w){
        assert hasPath(w) ;
        Vector<Integer> vec = path(w);
        for( int i = 0 ; i < vec.size() ; i ++ ){
            System.out.print(vec.elementAt(i));
            if( i == vec.size() - 1 )
                System.out.println();
            else
                System.out.print(" -> ");
        }
    }
    // 查看从s点到w点的最短路径长度
    // 若从s到w不可达，返回-1
    public int length(int w){
        assert w >= 0 && w < G.V();
        return ord[w];
    }
}