最近有关注到,在C/C++中,对于浮点数的四舍五入,与实际的有一些出入,我打算今天总结一下,并解释一下这是为啥,
好了,下面进入正题,都是干货哦,认真看完,留下你的赞,哈哈,
首先,说到四舍五入,就首先要想到取整函数,但是今天不说这些取整函数哦,就是来解释一下一些结果与不符和常理的结果。
四舍五入,大于5,就进位,小于5,就舍去,绝大多数的问题出在了5上面,这个5究竟特殊在哪里呢?
1,精度丢失
首先咱们来看一段代码
#include <stdio.h>
int main() {
double a = 80.845;
float b = 80.845f;
printf("a = %.2lf\n",a);
printf("b = %.2f\n",b);
return 0;
}这段代码的意思是,分别对80.845这个数保留两位小数打印,那结果都应该是80.85。对,按理来说就应该是这个答案。那我们运行一下看一下
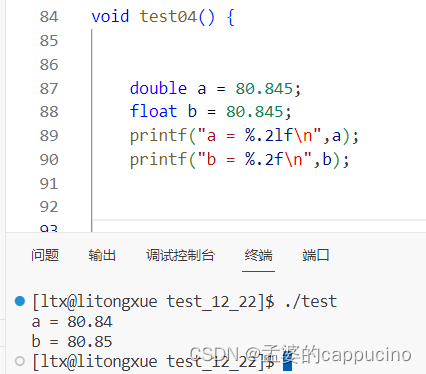
好的,我们看到了答案,b的答案是正常进行四舍五入了的,a是80.84,这是没有进行进位吗,
聪明的小伙伴已经注意到了,a是double类型的,b是float类型的,哈哈哈,问题是不是在这里呢。对的,问题就出在这里,因为double用8个字节进行存储数据,float是用4个字节存储数据,是不是他们在存储数据的时候出现了问题呢,咱们打印出来试一下
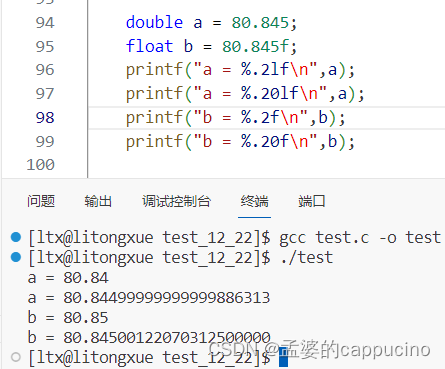
当我们打印20个小数位的时候,差距就出来了。(float类型的有效数据是7位,double是16位,其他的均是误差,可忽略,我们测试用的数据都是在有效范围内的)
我们发现,double中存储80.845的时候,存储的是80.84499999999999886313,float在存储80.845的时候,存储的是80.84500122070312500000,
没错,就是存储的锅,因为存储的数不是80.845,是80.844...,所以才没有进位,
那为什么会是这种结果呢,我们知道浮点数在内存中存储的时候,也是存储的二进制位,对于整数的二进制位我们都很熟悉,那么小数部分的二进制怎么表示呢,
//从二进制的权值表示不难推断:
// 0 0 0 0 . 0 0 0 0
// 2^3 2^2 2^1 2^0 2^-1 2^-2 2^-3 2^-4是这样表示的,所以我们要表示一个浮点数的小数部分的话,就需要去凑,举个例子
double a = 0.875;
// 0.875 : 0.5 + 0.25 + 0.125
// 2^-1 2^-2 2^-3
//所以用二进制表示就是 0.111看到这里大概就懂了,因为有些数是凑不出来的,比如说0.3,所以就产生了误差,但是计算机在尽力给我们凑了,保证误差尽可能的小,
那有的小伙伴就开始说了,是不是以后要判断一个数是否会四舍五入,就多打印几位出来,是不是就可以知道是不是会进位了,
我只能说大部分情况是可以的,但是我这篇文章还没完呢,还有一个标题呢,接着往下看
2,银行家舍入法
银行家舍入法,又叫做四舍六入五凑偶法,是由IEEE 754标准规定的浮点数取整算法,我们先来解释一下是什么意思
先来看一段代码
#include <stdio.h>
int main() {
double c = 80.25;
float d = 80.25;
printf("c = %.1lf\n",c);
printf("c = %.20lf\n",c);
printf("d = %.1f\n",d);
printf("d = %.20f\n",d);
return 0;
}代码很简单,就是对于80.25,保留一位小数打印,因为经过上面的解释,我们知道0.25是可以被精确表示的,不会存在精度丢失的情况,我们执行来看看
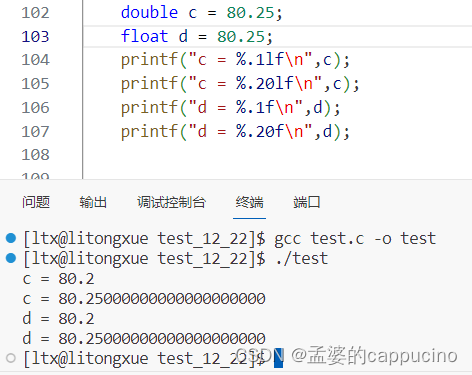
好的,我们看到80.25不管是double还是float类型都可以精确保存,没有精度丢失,但是还是没有进位,这是为啥
这就是银行家舍入算法,来解释一下:
银行家舍入法只有在被舍入位的值是5的时候,并且,舍入位的后面没有任何数据的时候,才会触发,这个时候会判断进位之后的那一位是否是偶数,如果是偶数,就进位,如果不是偶数,就选择不进位,可以理解成趋偶性。
80.25保留一位小数就刚好符合这两个条件。
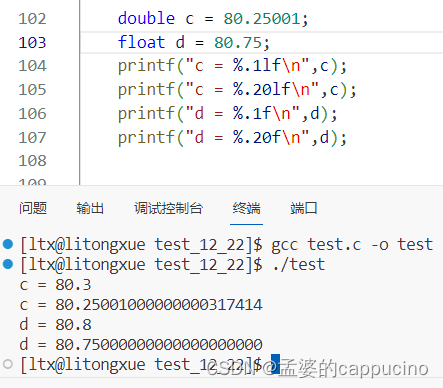
为了验证,我改了两个数据,
当数据是80.25001,内存中存储的这个数的二进制位5的后面还有数据,不符和银行家舍入法,所以就会进位,
当数据是80.75的时候,这个时候,也是可以精确表示的,没有精度丢失,舍入位是5,并且5之后没有其他数据,这个时候就会,触发银行家舍入法,趋偶性,就会选择进位,
结语
最后,我在gcc上跑完之后,又去vs2022上验证了一下,都是一样的,所以大胆食用,
关于这个算法,我自己的看法就是,为什么选择趋偶呢,是因为大多数偶数是不会发生精度丢失的,可以避免很多系统性误差,
我也查了很多资料,关于银行家舍入法。结果显示,银行家舍入法旨在减小舍入误差,以确保结果更接近数学期望,而且,金融和会计领域通常要求精确的数值计算,而银行家舍入法在这些领域中是常见的舍入方式。
最后的最后,希望我的这篇文章可以帮助到看了文章的你,
欢迎大家评论点赞转发,如果有什么错误,可以辛苦私信指出(麻烦了)!