通过上期学习,大家已经了解了非线性规划中无约束极值问题及其求解方法。本期小编将为大家介绍最优性条件,包括可行下降方向、库恩-塔克条件等内容。
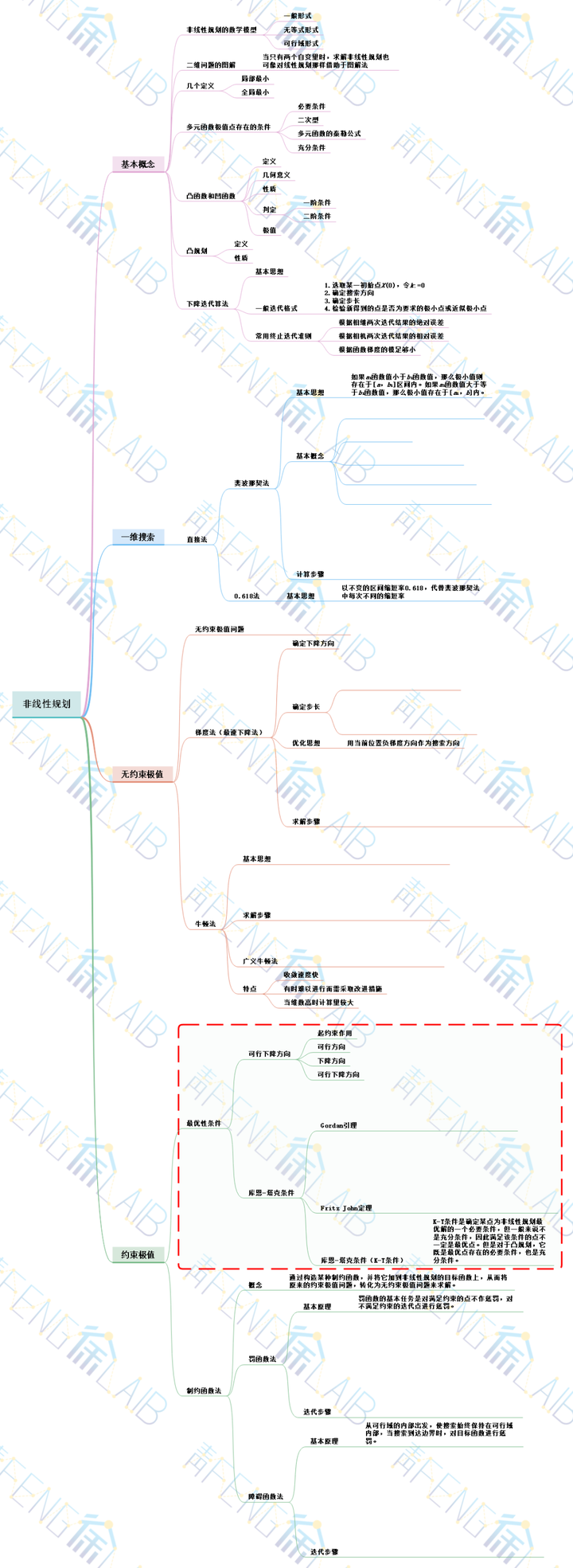
1 可行下降方向
起约束作用
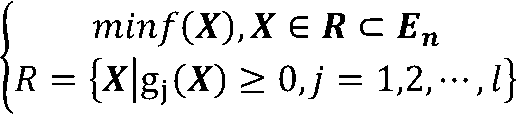
假定X(0)是上述问题的一个可行解,满足所有约束。对某约束条件gj(X)≥0来说,满足它有两种情况:
(1)gj(X)>0:此时X(0)在可行域内部,不在该约束条件形成的可行域边界上,则称该约束为X(0)点的不起作用约束(无效约束)。
(2)gj(X)=0:此时X(0)点处于由该约束条件形成的可行域边界上,则称该约束为X(0)点的起作用约束(有效约束)。
可行方向
设X(0)为任一可行点,对某一方向P来说,若存在实数λ0>0,使对任意的λ∈[0,λ0],均有X(0)+λP∈R成立,就称方向P为X(0)点的一个可行方向。
以J记X(0)点所有起作用约束下标集合,即
![]()
若P为X(0)点的可行方向,则存在λ0>0,使对任意λ∈[0,λ0],有
![]()
从而
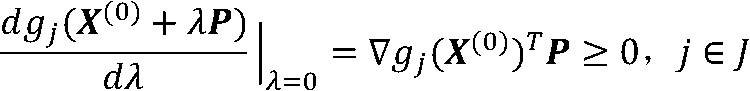
其中∇gj(X(0))为约束函数在点的梯度。
由泰勒展开式
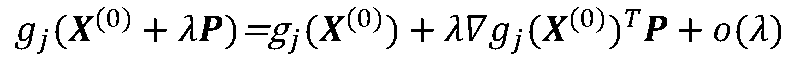
对X(0)点的所有起作用约束,当λ>0足够小时,只要
![]()
就有
![]()
此外,对X(0)点所有不起作用约束,gj(X(0))>0,由gj(X)的连续性,当λ>0足够小时,也有
![]()
所以,只要方向P满足上述梯度不等式,即可保证它是点的可行方向。
下降方向
设X(0)∈R,对某一方向P来说,若存在实数λ0'>0,使对任意的λ∈[0,λ0']均有下式成立
![]()
就称方向P为点的一个下降方向。
由泰勒展开式
![]()
当λ足够小时,只要∇f(X(0))TP<0,就有f(X(0)+λP)<f(X(0))。即只要方向P满足∇f(X(0))TP<0,就可保证它为X(0)点的下降方向。
可行下降方向
若X(0)点的某一方向P,既是该点的可行方向,又是该点的下降方向,那么就称它为这个点的可行下降方向。
设X(0)不是极小点,为求其极小点,继续搜索应沿该点的可行下降方向进行。显然,对X*来说,若该点不存在可行下降方向,它就可能是局部极小点,若存在可行下降方向,它就不是极小点。
定理4
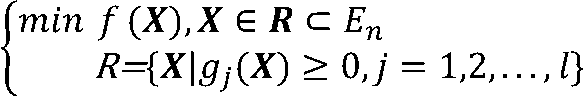
设X*是上述问题的一个局部极小点,f(X)在X*处可微,且

则在X*点不存在可行下降方向,从而不存在P同时满足
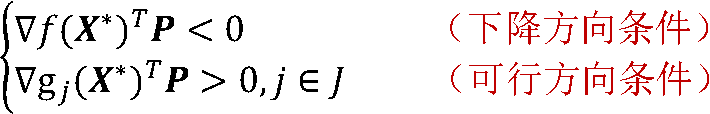
其中,指标集J={j | gj(X*)=0,1≤j≤l}
从几何上说,满足上式的方向P与该点目标函数负梯度方向的夹角成锐角,且与该点起作用约束梯度方向的夹角也成锐角。
2 库恩-塔克条件
Gordan引理
设A1,A2,...,Al为个n维向量,不存在向量P使
![]()
成立的充要条件是存在不全为零的非负实数μ1,μ2,...,μl,使
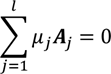
几何意义
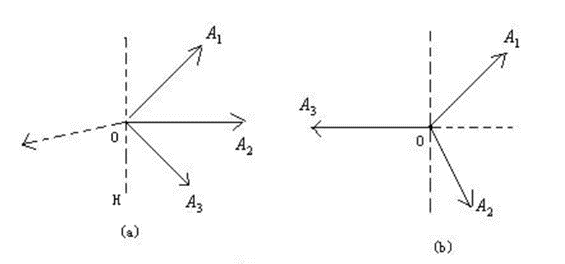
设A1,A2,A3是三个二维向量,若它们均位于某条直线H的同一侧,则可找到某一向量P,使AjTP<0(j=1,2,3)。但是,如果A1,A2,A3不在任一条直线的同一侧,就无法找到使AjTP<0(j=1,2,3)均满足的向量P,因为总可以放大或缩小各向量的长度,使之合成为零向量,即可找到不全为零的非负实数μj使
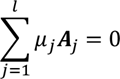
Fritz John定理
设X*是非线性规划的局部最优点,函数f(x)和gj(x)(j=1,2,...,l)在点X*有连续一阶偏导,则必然存在不全为零的数μ1,μ2,...,μl,使
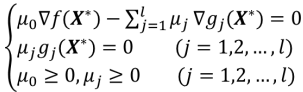
该定理给出了非线性规划的局部最优点应满足的必要条件,上式称为Fritz John条件,满足这个条件的点称为Fritz John点。
-
Fritz John条件是由Gordan引理矩阵展开得到。Gordan引理只对起作用约束做了说明,Fritz Join定理采用互补松弛条件将非作用约束引入,取对应参数为0改良得到。
-
判断一个点是不是Fritz John点的步骤就是找到对应点的函数梯度,带入公式看是否能找到不全为零的数使得方程成立。
如果μ0=0,∇f(x)就从Fritz John条件中消去,说明在所讨论的点X*处,起作用约束的梯度线性相关,这时Fritz John条件失效,因此需要对讨论点处起作用约束的梯度附加上线性无关的条件,以保证μ0>0,这样就引出了库恩-塔克条件。
库恩-塔克条件(K-T条件)

K-T条件是确定某点为非线性规划最优解的一个必要条件,但一般来说不是充分条件,因此满足该条件的点不一定是最优点。但是对于凸规划,它既是最优点存在的必要条件,也是充分条件。
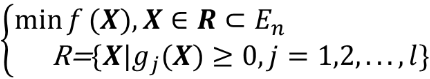
设X*是上述问题的局部极小点,函数f(x)和gj(x)(j=1,2,...,l)在X*点有连续一阶偏导,且X*处的所有起作用约束的梯度线性无关,则存在μ1*,μ2*,...,μl*,使
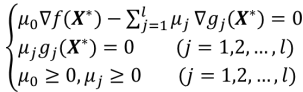
上述条件称为库恩-塔克条件,满足该条件的点叫库恩-塔克点。
考虑非线性规划
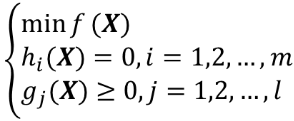
其中f(x)、h(x)、gj(x)都具有一阶连续偏导数,我们以
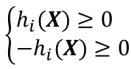
代替hi(x)=0,从而得到上述非线性规划的库恩-塔克条件:若X*是其极小点,且X*点所有起作用约束的梯度∇hi(X*)和∇gj(X*)线性无关,则存在向量Γ*=(γ1*,γ2*,...,γm*)T和M*=(μ1*,μ2*,...,μl*)T使下述条件成立:
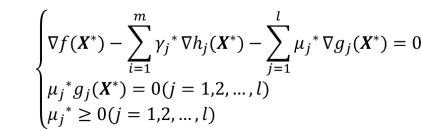
其中γ1*,γ2*,...,γm*和μ1*,μ2*,...,μl*称为广义拉格朗日乘子。
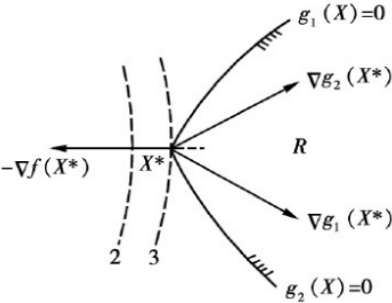
为加深对K-T条件的直观理解,考虑某非线性规划的可行解X(k),假定此处有两个起作用约束,g1(X(k))=0和g2(X(k))=0,若X(k)为极小点,则∇f(X(k))必处于∇g1(X(k))和∇g2(X(k))的夹角内。
【证明过程】
假设∇f(X(k))方向如图所示,沿g1(X(k))=0的方向函数值增大,沿g2(X(k))=0的方向函数值减小,即在X(k)点存在可行下降方向,它就不是极小点,与题设矛盾。由此可见,若X(k)是极小点,且此处起作用约束的梯度线性无关,则可∇f(X(k))将表示成∇g1(X(k))和∇g2(X(k))的非负线性组合,即存在μ1≥0,μ2≥0,使下式成立:
![]()
例题
用库恩-塔克条件解非线性规划
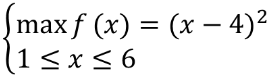
解:先将其转换为标准形式
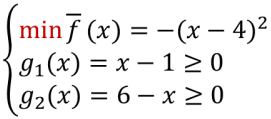
设库恩-塔克点为x*,各函数梯度为
![]()
对两个约束条件分别引入拉格朗日乘子μ1*和μ2*代入
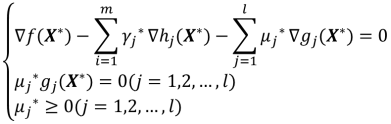
该问题的库恩-塔克条件如下
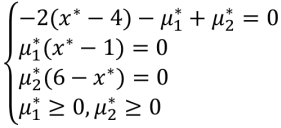
分别考虑一下几种情况:
(1)μ1*>0,μ2*>0:无解;(约束2,3无法同时成立)
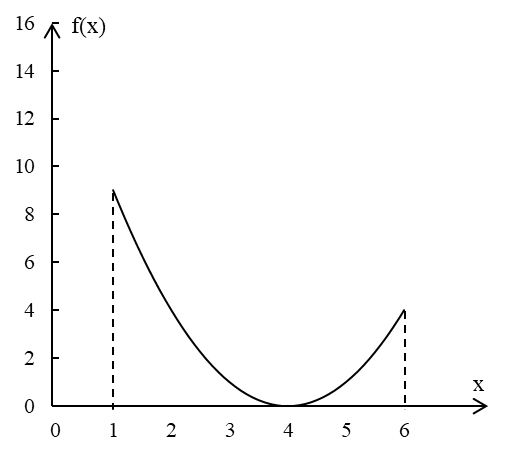
(2)μ1*>0,μ2*=0:x*=1,f(x*)=9;(约束2)
(3)μ1*=0,μ2*=0:x*=4,f(x*)=0;(约束1)
(4)μ1*=0,μ2*>0:x*=6,f(x*)=4。(约束3)
以上就是非线性规划中最优性条件的全部内容了,通过本节学习大家是否对可行下降方向与库恩-塔克条件有了一个大致的认识呢?下期小编将讲一讲与知识内容相关的逸闻趣事,为大家介绍为什么库恩-塔克条件又叫KKT条件,敬请关注!
作者 | 林若唯 唐京茹
责编 | 陈梦
审核 | 徐小峰






![[zabbix] zabbix监控](https://img-blog.csdnimg.cn/direct/5e2ec9e265984b4cb0c8c7bfc67b8cb1.png)