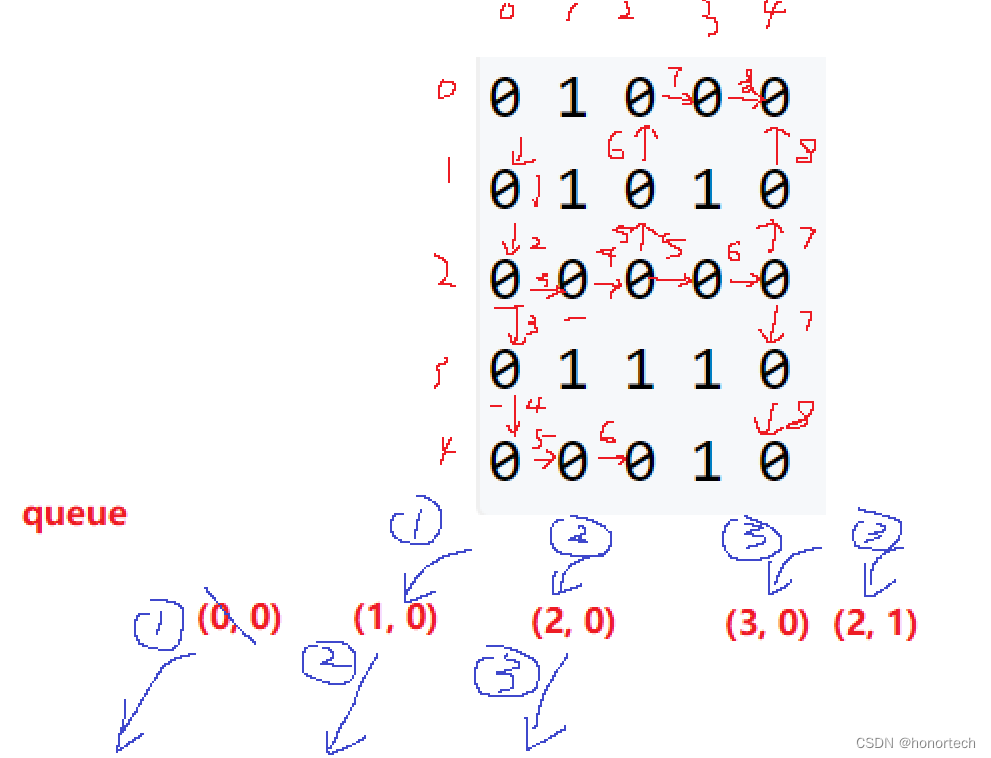
方法一 个人方法 排序+一次遍历:
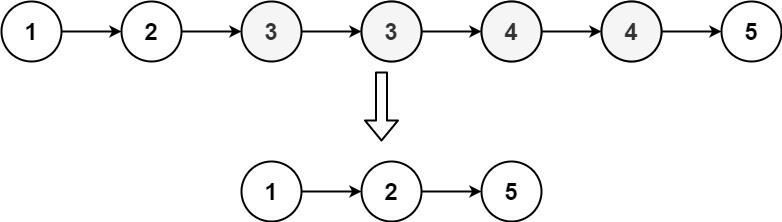
最小差值一定是出现在大小相邻的两个元素之间,所以将数组从小到大排序
循环求两元素之间的差值,先假设当前差值为最小差值,先往res数组里面push数据,当碰到更小差值的时候,把res清空,重新往res里push差值为新的最小差值的元素对
var minimumAbsDifference = function(arr) {
arr.sort((a,b)=>a-b)
let min=999,res=[]
for(let i=0;i<arr.length;i++){
if(arr[i+1]-arr[i]<min){
min=arr[i+1]-arr[i]
res=[]
res.push([arr[i],arr[i+1]])
}else if(arr[i+1]-arr[i]===min){
res.push([arr[i],arr[i+1]])
}
}
return res
};消耗时间和内存情况: