BFS

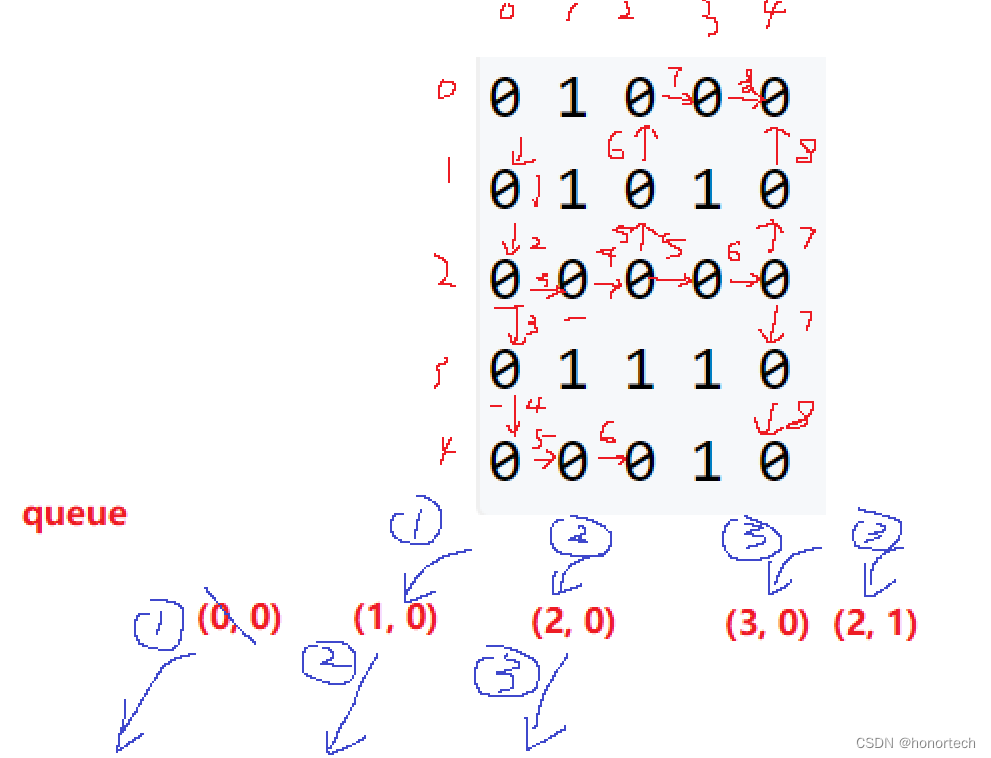
• BFS 重点就是要使用 队列 进行每一层的搜索
• 不同题目 队列中保存的元素形式都各不相同，并且也会用到其他辅助结构
• 走迷宫一题，队列中存的是每一层(当前步能走的所有坐标)的坐标，并保存了每一层对应走过的步数
• 八数码一题，队列中存的是每一层(当前x位置可以发生交换位置对应的交换后的结果)可能的交换后的序列，并保存了每种交换后的序列所对应的交换次数
• 二叉树的层序遍历就是 BFS

AcWing 844. 走迷宫

#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
const int N = 109, MAX = 0x3f3f3f3f;
int n, m, maze[N][N], ret, d[N][N];
// 队列的作用是将对头元素的下一层元素全部放入队列
queue<pair<int, int>> m_next; 
int bfs(int x, int y)
{
    int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
    m_next.push({x, y});
    maze[x][y] = 1;
    while(m_next.size())
    {
        pair<int, int> cur = m_next.front();
        m_next.pop();
        for (int i = 0; i < 4; i ++ )
        {
            int cx = cur.first + dx[i], cy = cur.second + dy[i];
            if(cx >= 0 && cx < n && cy >= 0 && cy < m && maze[cx][cy] == 0)
            {
                m_next.push({cx, cy});
                maze[cx][cy] = 1;
                d[cx][cy] = d[cur.first][cur.second] + 1;
            }
        }
    }
    return d[n - 1][m - 1];
}
int main()
{
    cin >> n >> m;
    for (int i = 0; i < n; i ++ )
        for (int j = 0; j < m; j ++ )
            cin >> maze[i][j];
    cout << bfs(0, 0);
    return 0;
}

AcWing 845. 八数码

#include <iostream>
#include <cstring>
#include <algorithm>
#include <string>
#include <queue>
#include <unordered_map>
using namespace std;
queue<string> m_next;
unordered_map<string, int> m_step;
char grid[3][3];
string str;
int main()
{
    int index = 0;
    for(int i = 0; i < 3; ++i)
    {
        for(int j = 0; j < 3; ++j)
        {
            cin >> grid[i][j];
            str += grid[i][j];
        }
    } 
    m_next.push(str);
    m_step[str] = 0;
    int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
    while (m_next.size())
    {
        string cur = m_next.front();
        m_next.pop();
        int step = m_step[cur];
        if(cur == "12345678x")
        {
            cout << m_step[cur];
            return 0;
        }
        int xcur = cur.find('x');
        for(int i = 0; i < 4; ++i)
        {
            int cx = xcur / 3 + dx[i], cy = xcur % 3 + dy[i];
            if(cx >= 0 && cx < 3 && cy >= 0 && cy < 3)
            {
                swap(cur[xcur], cur[cx * 3 + cy]);
                if(m_step.find(cur) == m_step.end())
                {
                    m_step[cur] = step + 1;
                    m_next.push(cur);
                }
                // 为不影响其他可能发生交换的位置，需要还原
                swap(cur[xcur], cur[cx * 3 + cy]);
            } 
        }
    }
    cout << -1;
    return 0;
}