一、贪心算法
贪心算法,又称贪婪算法,是算法设计中的一种思想
其期待每一个阶段都是局部最优的选择,从而达到全局最优,但是结果并不一定是最优的
举个零钱兑换的例子,如果你有1元、2元、5元的钱币数张,用于兑换一定的金额,但是要求兑换的钱币张数最少
如果现在你要兑换11元,按照贪心算法的思想,先选择面额最大的5元钱币进行兑换,那么就得到11 = 5 + 5 + 1 的选择,这种情况是最优的
但是如果你手上钱币的面额为1、3、4,想要兑换6元,按照贪心算法的思路,我们会 6 = 4 + 1 + 1这样选择,这种情况结果就不是最优的选择
从上面例子可以看到,贪心算法存在一些弊端,使用到贪心算法的场景,都会存在一个特性:
一旦一个问题可以通过贪心法来解决,那么贪心法一般是解决这个问题的最好办法
至于是否选择贪心算法,主要看是否有如下两大特性:
- 贪心选择:当某一个问题的整体最优解可通过一系列局部的最优解的选择达到,并且每次做出的选择可以依赖以前做出的选择,但不需要依赖后面需要做出的选择
- 最优子结构:如果一个问题的最优解包含其子问题的最优解,则此问题具备最优子结构的性质。问题的最优子结构性质是该问题是否可以用贪心算法求解的关键所在
二、回溯算法
回溯算法,也是算法设计中的一种思想,是一种渐进式寻找并构建问题解决方式的策略
回溯算法会先从一个可能的工作开始解决问题,如果不行,就回溯并选择另一个动作,知道将问题解决
使用回溯算法的问题,有如下特性:
- 有很多路,例如一个矩阵的方向或者树的路径
- 在这些的路里面,有死路也有生路,思路即不符合题目要求的路,生路则符合
- 通常使用递归来模拟所有的路
常见的伪代码如下:
result = []
function backtrack(路径, 选择列表):
if 满足结束条件:
result.add(路径)
return
for 选择 of 选择列表:
做选择
backtrack(路径, 选择列表)
撤销选择
重点解决三个问题:
- 路径:也就是已经做出的选择
- 选择列表
- 结束条件
例如经典使用回溯算法为解决全排列的问题,如下:
一个不含重复数字的数组 nums ,我们要返回其所有可能的全排列,解决这个问题的思路是:
- 用递归模拟所有的情况
- 遇到包含重复元素的情况则回溯
- 收集到所有到达递归终点的情况,并返回、

用代码表示则如下:
var permute = function(nums) {
const res = [], path = [];
backtracking(nums, nums.length, []);
return res;
function backtracking(n, k, used) {
if(path.length === k) {
res.push(Array.from(path));
return;
}
for (let i = 0; i < k; i++ ) {
if(used[i]) continue;
path.push(n[i]);
used[i] = true; // 同支
backtracking(n, k, used);
path.pop();
used[i] = false;
}
}
};
三、总结
前面也初步了解到分而治之、动态规划,现在再了解到贪心算法、回溯算法
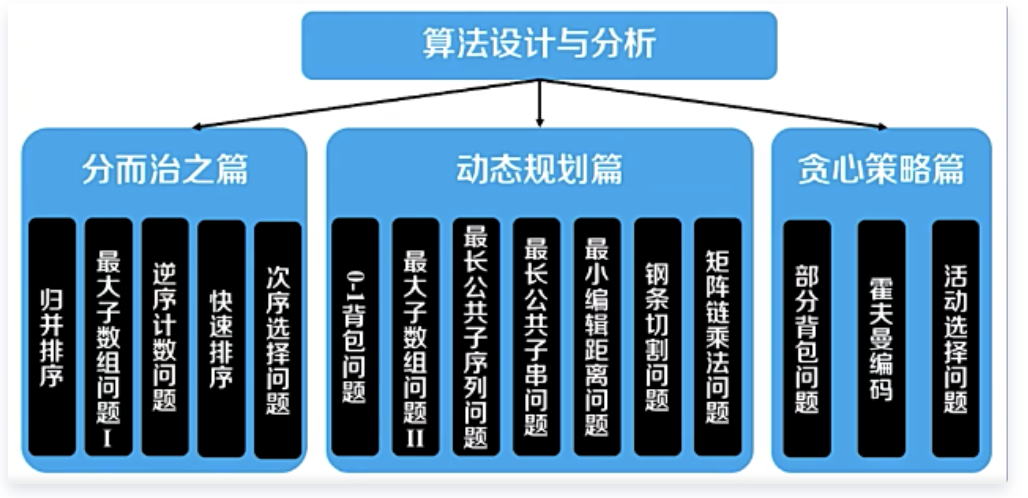
其中关于分而治之、动态规划、贪心策略三者的求解思路如下:

其中三者对应的经典问题如下图:
参考文献
- https://zh.wikipedia.org/wiki/%E8%B4%AA%E5%BF%83%E7%AE%97%E6%B3%95
- https://leetcode-cn.com/problems/permutations/solution/dai-ma-sui-xiang-lu-dai-ni-xue-tou-hui-s-mfrp/
- https://cloud.tencent.com/developer/article/1767046
更多资源==> GitHub