redis数据结构源码分析—

redis数据结构源码分析——跳表zset

news2024/11/18 4:45:12

文章目录

跳表的基本思想
- 特点
- 节点与结构
- 跳跃表节点zskiplistNode
- - 属性
- 跳跃表链表
- - 属性
跳表的设计思想和优势
API解析
- zslCreate（创建跳跃表）
- zslCreateNode（创建节点）
- zslGetRank（查找排位）
- zslDelete（删除节点）

跳表的基本思想

Skip List(跳跃列表)这种随机的数据结构，可以看做是一个二叉树的变种，它在性能上与红黑树、AVL树很相近；但是Skip List(跳跃列表)的实现相比前两者要简单很多，目前Redis的zset实现采用了Skip List(跳跃列表)。
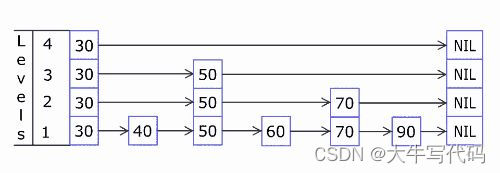
在这里插入图片描述

特点

1、分层，每层由有序链表构成
2、头节点在每层出现
3、某个节点如果在上层出现，那在下层也出现
4、节点的层数是随机的

节点与结构

跳跃表节点zskiplistNode

/* ZSETs use a specialized version of Skiplists */
typedef struct zskiplistNode {
    sds ele;
    double score;
    struct zskiplistNode *backward;
    struct zskiplistLevel {
        struct zskiplistNode *forward;
        unsigned long span;
    } level[];
} zskiplistNode;

属性

ele：存储字符串数据
score：存储排序分值
*backward：指针，指向当前节点最底层的前一个节点
level[]：柔性数组，随机生成1-64的值
forward：指向本层下一个节点
span：本层下个节点到本节点的元素个数

跳跃表链表

typedef struct zskiplist {
    struct zskiplistNode *header, *tail;
    unsigned long length;
    int level;
} zskiplist;

属性

header，tail：头节点和尾节点
length：跳跃表长度（不包括头节点）
tail：跳跃表高度

跳表的设计思想和优势

1、能够同时拥有链表和数优势的数据结构，既有链表插入快的特点又有数组查询快的特点
2、随机跨越层数
3、最底层的链表是双向链表，包含所有元素
4、对于有序链表查询优化，相比较于平衡数来说，更好实现
5、内存占用上来看，相比较于平衡数会更少

API解析

Tip：以下的zsl为zskiplist

zslCreate（创建跳跃表）

/* Create a new skiplist. */
zskiplist *zslCreate(void) {
    int j;
    zskiplist *zsl;

    zsl = zmalloc(sizeof(*zsl));
    zsl->level = 1;
    zsl->length = 0;
    zsl->header = zslCreateNode(ZSKIPLIST_MAXLEVEL,0,NULL);
    for (j = 0; j < ZSKIPLIST_MAXLEVEL; j++) {
        zsl->header->level[j].forward = NULL;
        zsl->header->level[j].span = 0;
    }
    zsl->header->backward = NULL;
    zsl->tail = NULL;
    return zsl;
}

大致流程：
1、定义一个zsl，申请内存，赋初始值
2、调用zslCreateNode创建出头节点
3、每层头节点赋初始值
4、尾节点赋null值

zslCreateNode（创建节点）

/* Create a skiplist node with the specified number of levels.
 * The SDS string 'ele' is referenced by the node after the call. */
zskiplistNode *zslCreateNode(int level, double score, sds ele) {
    zskiplistNode *zn =
        zmalloc(sizeof(*zn)+level*sizeof(struct zskiplistLevel));
    zn->score = score;
    zn->ele = ele;
    return zn;
}

大致流程：
1、申请内存（节点内存和柔性数组的内存）
2、属性赋值

zslGetRank（查找排位）

排位就是累积跨越的节点数量

unsigned long zslGetRank(zskiplist *zsl, double score, sds ele) {
    zskiplistNode *x;
    unsigned long rank = 0;
    int i;

    x = zsl->header;
    for (i = zsl->level-1; i >= 0; i--) {
        while (x->level[i].forward &&
            (x->level[i].forward->score < score ||
                (x->level[i].forward->score == score &&
                sdscmp(x->level[i].forward->ele,ele) <= 0))) {
            rank += x->level[i].span;
            x = x->level[i].forward;
        }

        /* x might be equal to zsl->header, so test if obj is non-NULL */
        if (x->ele && x->score == score && sdscmp(x->ele,ele) == 0) {
            return rank;
        }
    }
    return 0;
}

大致流程：
1、从最上层开始遍历节点并对比元素，对比score
2、如果当前分值大雨下一个分值，则累加span（比对分值，如果分值一样就比对ele）
3、指向本层的下一个节点
4、如果找到了，也就是ele相同，则返回

zslDelete（删除节点）

int zslDelete(zskiplist *zsl, double score, sds ele, zskiplistNode **node) {
    zskiplistNode *update[ZSKIPLIST_MAXLEVEL], *x;
    int i;

    x = zsl->header;
    for (i = zsl->level-1; i >= 0; i--) {
        while (x->level[i].forward &&
                (x->level[i].forward->score < score ||
                    (x->level[i].forward->score == score &&
                     sdscmp(x->level[i].forward->ele,ele) < 0)))
        {
            x = x->level[i].forward;
        }
        update[i] = x;
    }
    /* We may have multiple elements with the same score, what we need
     * is to find the element with both the right score and object. */
    x = x->level[0].forward;
    if (x && score == x->score && sdscmp(x->ele,ele) == 0) {
        zslDeleteNode(zsl, x, update);
        if (!node)
            zslFreeNode(x);
        else
            *node = x;
        return 1;
    }
    return 0; /* not found */
}