参考资料:用python动手学统计学
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
import seaborn as sns
data_set=pd.read_csv(r"C:\python统计学\3-4-1-fish_length_100000.csv")['length'] #此处将文件路径改为自己的路径即可1、抽样
为了保证数据分析的可复现性,使用了随机种子。
np.random.choice()的用法参考:https://blog.csdn.net/maizeman126/article/details/135572042

2、计算样本均值

3、计算总体统计量
相关函数用法参照:python统计分析——单变量描述统计-CSDN博客
mean_t=np.mean(data_set)
std_t=np.std(data_set,ddof=0)
var_t=np.var(data_set,ddof=0)
max_t=np.max(data_set)
min_t=np.min(data_set)
print('总体均值:',mean_t)
print('总体标准差:',std_t)
print('总体方差:',var_t)
print('最大值:',max_t)
print('最小值:',min_t)
4、绘制总体的直方图:
直方图的绘制参照:
python统计分析——直方图(plt.hist)_python统计直方图-CSDN博客
python统计分析——直方图(sns.histplot)-CSDN博客
python统计分析——直方图(df.hist)_python df.hist()-CSDN博客
sns.set()
sns.histplot(data_set,kde=False,color='black')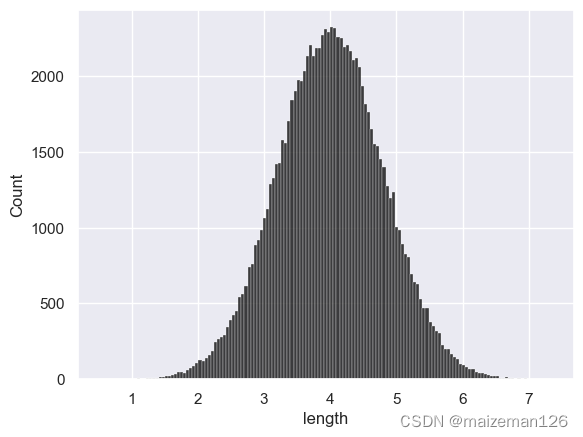
根据总体统计量计算和直方图直观查看,目前可以暂时认为:总体的概率分布服从均值为4,方差为0.64的正态分布,数值的分布范围基本在1-7之间。
5、绘制均值为4,方差为0.64,数据范围为1-7的正态分布的概率密度曲线
5.1 准备1-7上以0.1为公差的等差数列。(注意np.arange函数应用中仍然遵循包左不包右的原则)
x=np.arange(start=1,stop=7.1,step=0.1)
5.2 用stats.norm.pdf计算概率密度。
stats.norm.pdf()函数中,x为分位数,loc表示均值,scale表示标准差(注意不是方差),结果表示取值x时对应的概率密度。
from scipy import stats
pro_d=stats.norm.pdf(x=x,loc=4,scale=0.8)
pro_d
5.3 绘制概率密度曲线
plt.plot(x,pro_d,color='k') #k表示颜色black的简写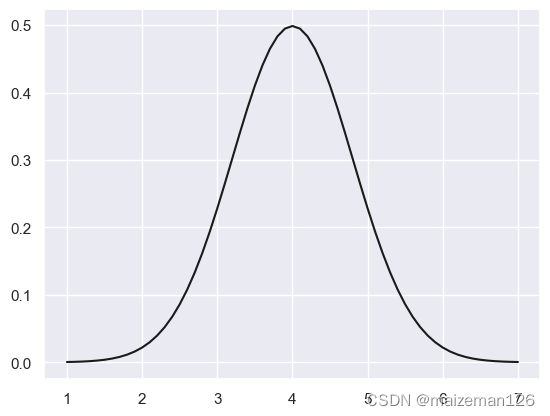
5.4 将总体直方图和正态分布概率密度函数放到一个中显示:
sns.histplot(data_set,stat='density',kde=False)
plt.plot(x,pro_d,color='k')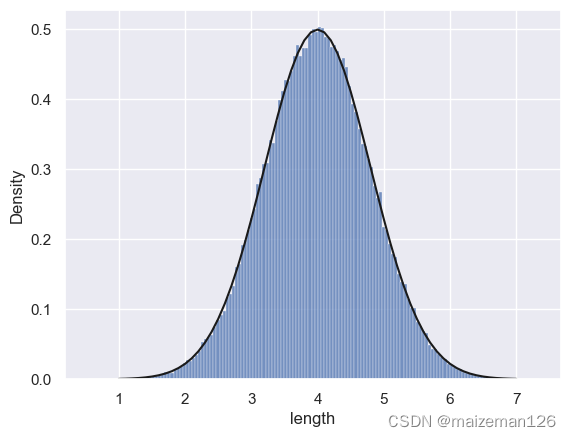
根据上图可以看出:正态分布的概率密度和总体分布的概率密度几乎吻合,因此可以认为总体服从正态分布。