总结

• 这周据说难度对标abc，根本扯淡。。
• E比较有难度，D赛中没想出来正数有啥用，直接前缀和莽F交了。
• A 模拟
• B 模拟
• C 模拟
• D 滑窗
• E 数学找规律
• F 前缀和+有序集合
• 

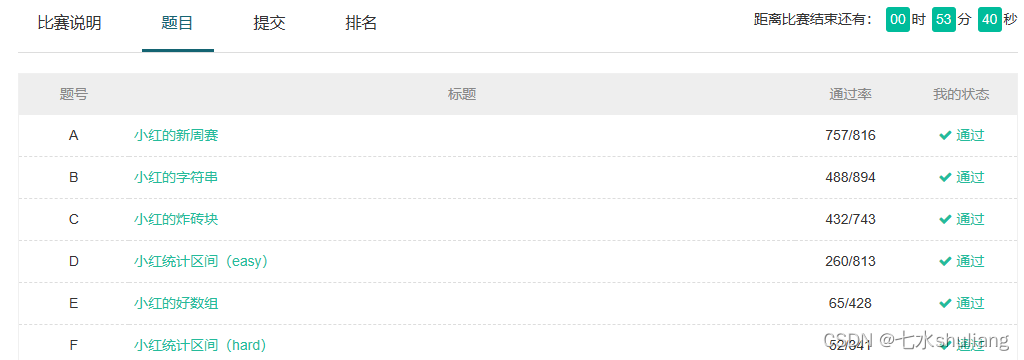
A\B

链接: 小红的新周赛
链接: 小红的字符串

1. 题目描述

2. 思路分析

• 按题意模拟。

3. 代码实现

def solve():
    print(sum(RI()))

def solve():
    s, = RS()
    ans = []
    for i in range(len(s)-1):
        ans.append(s[i:i+2])
    ans.sort()
    print(*ans,sep='\n')

小红的炸砖块

链接: 小红的炸砖块

1. 题目描述

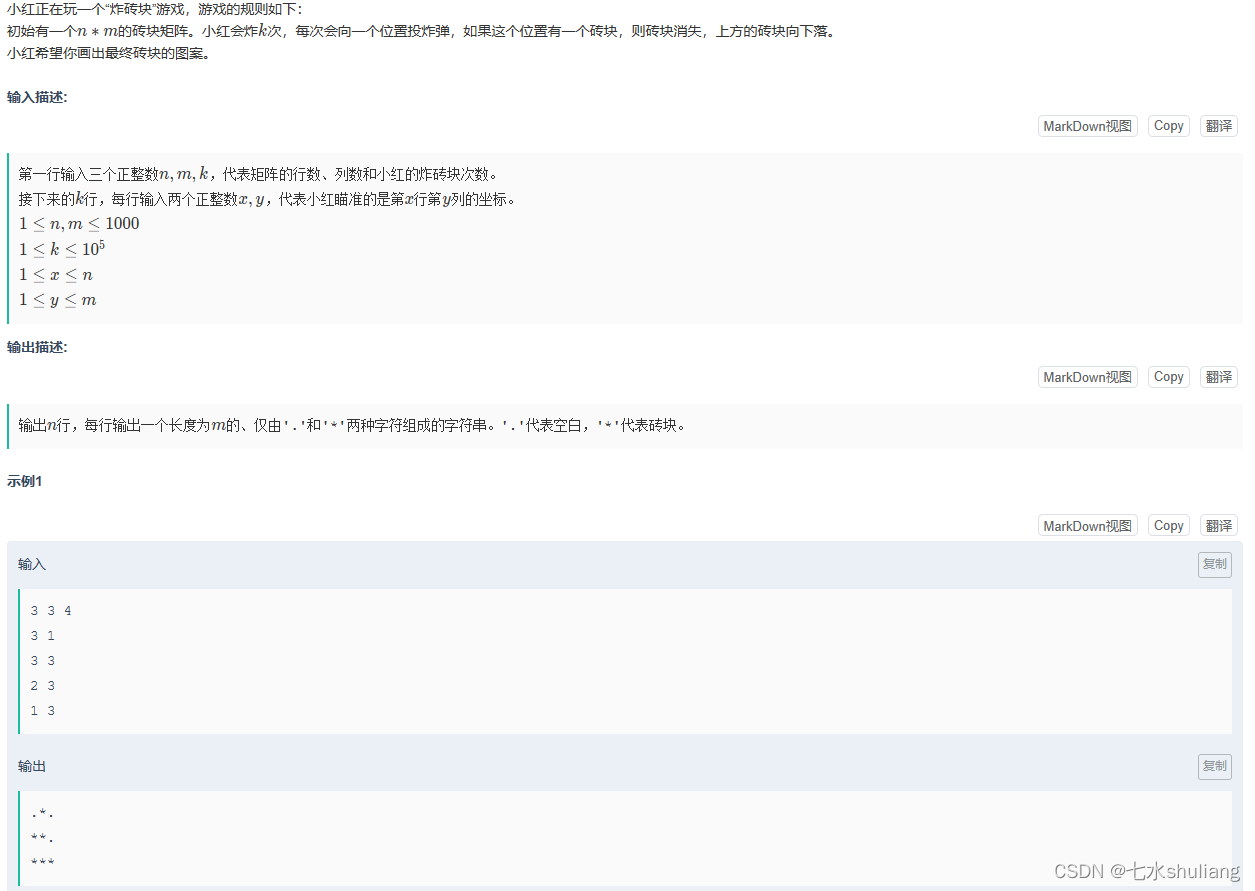
2. 思路分析

• 用一个长为列宽的数组a记录每列当前最高砖块的行坐标即可。
• 炸x,y的时候可以判断a[y]<=x，即y列的x位置是否有砖块。

3. 代码实现

def solve():
    m,n,k = RI()
    a = [0]*n
    for _ in range(k):
        x,y = RI()
        x -= 1
        y -= 1
        if a[y] <= x:
            a[y] += 1
    for i in range(m):
        ans = ['.']*n
        for j in range(n):
            if a[j] <= i:
                ans[j] = '*'
        print(*ans,sep='')

小红统计区间（easy）

链接: 小红统计区间（easy）

1. 题目描述

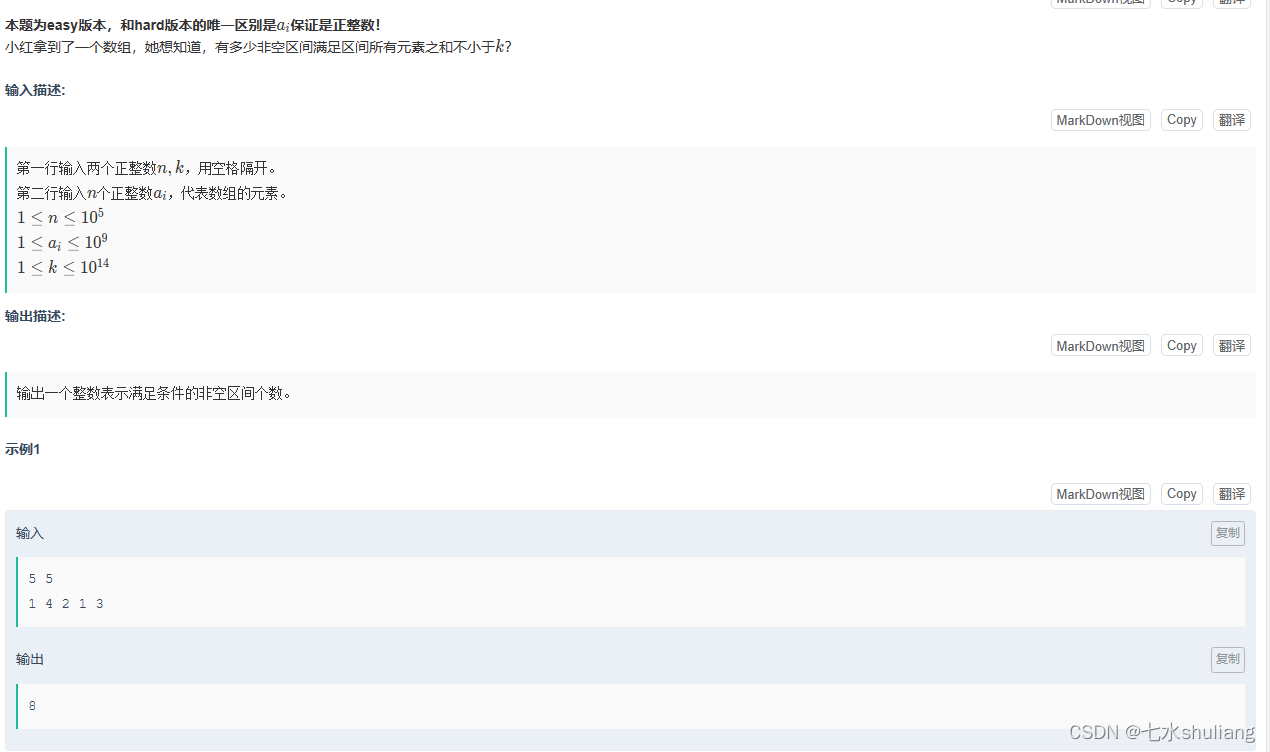
2. 思路分析

• 全是正数，那么可以滑窗，复杂度O(n)
• 维护[j,i]区间，使这个区间和恰好不到k，那么j向左一下就能到k，所以把所有j（窗首）加起来即可。
• 注意由于这个窗可能为空，所以双指针写法比队列方便。

3. 代码实现

#       ms
def solve2():
    n, k = RI()
    a = RILST()
    s = ans = 0
    q = deque()
    for i, v in enumerate(a):
        q.append(i)
        s += v
        while q and s >= k:
            s -= a[q.popleft()]
        ans += q[0] if q else i + 1

    print(ans)


def solve():
    n, k = RI()
    a = RILST()
    j = s = ans = 0

    for i, v in enumerate(a):
        s += v
        while j <= i and s >= k:
            s -= a[j]
            j += 1

        ans += j

    print(ans)

小红的好数组

链接: 小红的好数组

1. 题目描述

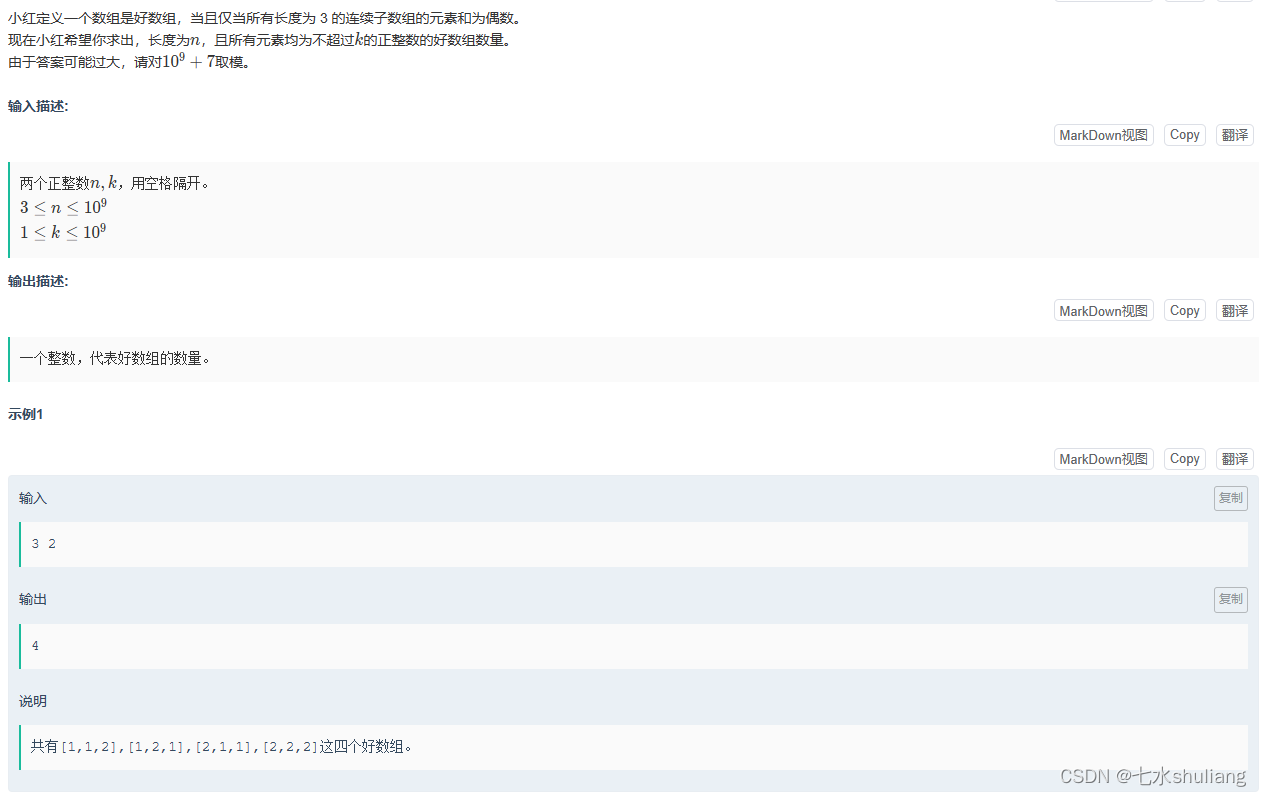
2. 思路分析

• 长为三的子段和全是偶数的话，显然可以所有数据全填偶数。而1~k里一共m=k//2个偶数,每个位置填任意偶数是独立的。显然方案数是pow(m,n)。
• 同理，在这些位置中选一些奇数，每个位置有x=k-m个奇数，也是独立事件。只需讨论一下奇数偶数的位置和个数即可。
• 在纸上画了一下，发现合法好数组一定是121 121 121 …（这里12代表奇数偶数） 三个一循环的数，且可以从中任意位置截取。
• 即开始位置共有三种：[1]21121121…；[2]11211211…;[1]12112112…。
• 分别讨论这三种，然后计算1和2的数量即可，这里我只计算2的数量m（因为每个循环节里只有1个2），取个模分类讨论即可。那么1的数量就是n-m。

3. 代码实现

def solve():
    n, k = RI()
    a, b = k // 2, (k + 1) // 2  # 1~k的偶数个数，奇数个数
    # 121 121 121 三个一循环
    ans = pow(a, n, MOD)  # 全填偶数
    x, y = divmod(n, 3)
    # 121开头
    two = x + int(y >= 2)
    ans += pow(a, two, MOD) * pow(b, n - two, MOD) % MOD
    # 211开头
    two = x + int(y >= 1)
    ans += pow(a, two, MOD) * pow(b, n - two, MOD) % MOD
    # 112开头
    two = x
    ans += pow(a, two, MOD) * pow(b, n - two, MOD) % MOD

    print(ans % MOD)

小红统计区间（hard）

链接: 小红统计区间（hard）

1. 题目描述

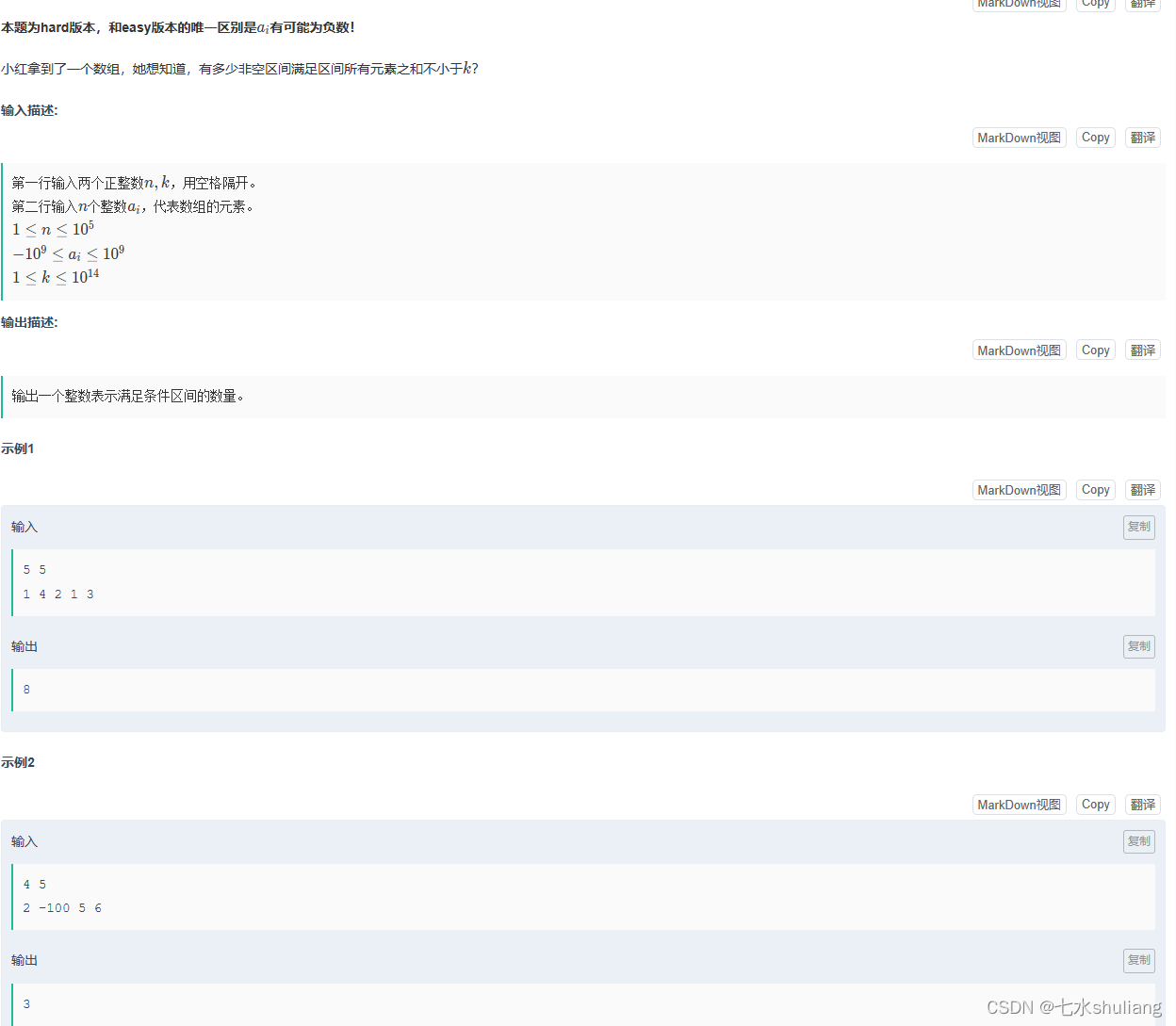
2. 思路分析

• 看到字段和，首先想到前缀和。s[i…j] = pre[j+1]-pre[i] (pre前补0）
• 那么对于每个j，其实就是找前边满足<=pre[j+1]-k的数量，这可以用有序集合二分来解决。

3. 代码实现

class CuteSortedList:
    def __init__(self, iterable=[], _load=200):
        """Initialize sorted list instance."""
        values = sorted(iterable)
        self._len = _len = len(values)
        self._load = _load
        self._lists = _lists = [values[i:i + _load] for i in range(0, _len, _load)]
        self._list_lens = [len(_list) for _list in _lists]
        self._mins = [_list[0] for _list in _lists]
        self._fen_tree = []
        self._rebuild = True

    def _fen_build(self):
        """Build a fenwick tree instance."""
        self._fen_tree[:] = self._list_lens
        _fen_tree = self._fen_tree
        for i in range(len(_fen_tree)):
            if i | i + 1 < len(_fen_tree):
                _fen_tree[i | i + 1] += _fen_tree[i]
        self._rebuild = False

    def _fen_update(self, index, value):
        """Update `fen_tree[index] += value`."""
        if not self._rebuild:
            _fen_tree = self._fen_tree
            while index < len(_fen_tree):
                _fen_tree[index] += value
                index |= index + 1

    def _fen_query(self, end):
        """Return `sum(_fen_tree[:end])`."""
        if self._rebuild:
            self._fen_build()

        _fen_tree = self._fen_tree
        x = 0
        while end:
            x += _fen_tree[end - 1]
            end &= end - 1
        return x

    def _fen_findkth(self, k):
        """Return a pair of (the largest `idx` such that `sum(_fen_tree[:idx]) <= k`, `k - sum(_fen_tree[:idx])`)."""
        _list_lens = self._list_lens
        if k < _list_lens[0]:
            return 0, k
        if k >= self._len - _list_lens[-1]:
            return len(_list_lens) - 1, k + _list_lens[-1] - self._len
        if self._rebuild:
            self._fen_build()

        _fen_tree = self._fen_tree
        idx = -1
        for d in reversed(range(len(_fen_tree).bit_length())):
            right_idx = idx + (1 << d)
            if right_idx < len(_fen_tree) and k >= _fen_tree[right_idx]:
                idx = right_idx
                k -= _fen_tree[idx]
        return idx + 1, k

    def _delete(self, pos, idx):
        """Delete value at the given `(pos, idx)`."""
        _lists = self._lists
        _mins = self._mins
        _list_lens = self._list_lens

        self._len -= 1
        self._fen_update(pos, -1)
        del _lists[pos][idx]
        _list_lens[pos] -= 1

        if _list_lens[pos]:
            _mins[pos] = _lists[pos][0]
        else:
            del _lists[pos]
            del _list_lens[pos]
            del _mins[pos]
            self._rebuild = True

    def _loc_left(self, value):
        """Return an index pair that corresponds to the first position of `value` in the sorted list."""
        if not self._len:
            return 0, 0

        _lists = self._lists
        _mins = self._mins

        lo, pos = -1, len(_lists) - 1
        while lo + 1 < pos:
            mi = (lo + pos) >> 1
            if value <= _mins[mi]:
                pos = mi
            else:
                lo = mi

        if pos and value <= _lists[pos - 1][-1]:
            pos -= 1

        _list = _lists[pos]
        lo, idx = -1, len(_list)
        while lo + 1 < idx:
            mi = (lo + idx) >> 1
            if value <= _list[mi]:
                idx = mi
            else:
                lo = mi

        return pos, idx

    def _loc_right(self, value):
        """Return an index pair that corresponds to the last position of `value` in the sorted list."""
        if not self._len:
            return 0, 0

        _lists = self._lists
        _mins = self._mins

        pos, hi = 0, len(_lists)
        while pos + 1 < hi:
            mi = (pos + hi) >> 1
            if value < _mins[mi]:
                hi = mi
            else:
                pos = mi

        _list = _lists[pos]
        lo, idx = -1, len(_list)
        while lo + 1 < idx:
            mi = (lo + idx) >> 1
            if value < _list[mi]:
                idx = mi
            else:
                lo = mi

        return pos, idx

    def add(self, value):
        """Add `value` to sorted list."""
        _load = self._load
        _lists = self._lists
        _mins = self._mins
        _list_lens = self._list_lens

        self._len += 1
        if _lists:
            pos, idx = self._loc_right(value)
            self._fen_update(pos, 1)
            _list = _lists[pos]
            _list.insert(idx, value)
            _list_lens[pos] += 1
            _mins[pos] = _list[0]
            if _load + _load < len(_list):
                _lists.insert(pos + 1, _list[_load:])
                _list_lens.insert(pos + 1, len(_list) - _load)
                _mins.insert(pos + 1, _list[_load])
                _list_lens[pos] = _load
                del _list[_load:]
                self._rebuild = True
        else:
            _lists.append([value])
            _mins.append(value)
            _list_lens.append(1)
            self._rebuild = True

    def discard(self, value):
        """Remove `value` from sorted list if it is a member."""
        _lists = self._lists
        if _lists:
            pos, idx = self._loc_right(value)
            if idx and _lists[pos][idx - 1] == value:
                self._delete(pos, idx - 1)

    def remove(self, value):
        """Remove `value` from sorted list; `value` must be a member."""
        _len = self._len
        self.discard(value)
        if _len == self._len:
            raise ValueError('{0!r} not in list'.format(value))

    def pop(self, index=-1):
        """Remove and return value at `index` in sorted list."""
        pos, idx = self._fen_findkth(self._len + index if index < 0 else index)
        value = self._lists[pos][idx]
        self._delete(pos, idx)
        return value

    def bisect_left(self, value):
        """Return the first index to insert `value` in the sorted list."""
        pos, idx = self._loc_left(value)
        return self._fen_query(pos) + idx

    def bisect_right(self, value):
        """Return the last index to insert `value` in the sorted list."""
        pos, idx = self._loc_right(value)
        return self._fen_query(pos) + idx

    def count(self, value):
        """Return number of occurrences of `value` in the sorted list."""
        return self.bisect_right(value) - self.bisect_left(value)

    def __len__(self):
        """Return the size of the sorted list."""
        return self._len

    # def __getitem__(self, index):
    #     """Lookup value at `index` in sorted list."""
    #     pos, idx = self._fen_findkth(self._len + index if index < 0 else index)
    #     return self._lists[pos][idx]
    def __getitem__(self, index):
        """Lookup value at `index` in sorted list."""
        if isinstance(index, slice):
            _lists = self._lists
            start, stop, step = index.indices(self._len)
            if step == 1 and start < stop:  # 如果是正向的步进1，找到起起止点，然后把中间的拼接起来即可
                if start == 0 and stop == self._len:  # 全部
                    return reduce(iadd, self._lists, [])
                start_pos, start_idx = self._fen_findkth(start)
                start_list = _lists[start_pos]
                stop_idx = start_idx + stop - start

                # Small slice optimization: start index and stop index are
                # within the start list.

                if len(start_list) >= stop_idx:
                    return start_list[start_idx:stop_idx]

                if stop == self._len:
                    stop_pos = len(_lists) - 1
                    stop_idx = len(_lists[stop_pos])
                else:
                    stop_pos, stop_idx = self._fen_findkth(stop)

                prefix = _lists[start_pos][start_idx:]
                middle = _lists[(start_pos + 1):stop_pos]
                result = reduce(iadd, middle, prefix)
                result += _lists[stop_pos][:stop_idx]
                return result
            if step == -1 and start > stop:  # 如果是负向的步进1，直接翻转调用自己再翻转即可
                result = self.__getitem__(slice(stop + 1, start + 1))
                result.reverse()
                return result

            indices = range(start, stop, step)  # 若不是步进1，只好一个一个取
            return list(self.__getitem__(index) for index in indices)

        else:
            pos, idx = self._fen_findkth(self._len + index if index < 0 else index)
            return self._lists[pos][idx]

    def __delitem__(self, index):
        """Remove value at `index` from sorted list."""
        pos, idx = self._fen_findkth(self._len + index if index < 0 else index)
        self._delete(pos, idx)

    def __contains__(self, value):
        """Return true if `value` is an element of the sorted list."""
        _lists = self._lists
        if _lists:
            pos, idx = self._loc_left(value)
            return idx < len(_lists[pos]) and _lists[pos][idx] == value
        return False

    def __iter__(self):
        """Return an iterator over the sorted list."""
        return (value for _list in self._lists for value in _list)

    def __reversed__(self):
        """Return a reverse iterator over the sorted list."""
        return (value for _list in reversed(self._lists) for value in reversed(_list))

    def __repr__(self):
        """Return string representation of sorted list."""
        return 'SortedList({0})'.format(list(self))




#       ms
def solve():
    n, k = RI()
    a = RILST()
    s = ans = 0
    """
    y-x>=k
    x <= y-k
    """
    sl = CuteSortedList([0])
    for v in a:
        s += v
        # print(s,sl)
        ans += sl.bisect_right(s-k)
        sl.add(s)
    print(ans)

六、参考链接

• 无