题目描述
输入一个十进制整数n,输出对应的二进制整数。常用的转换方法为“除2取余,倒序排列”。将一个十进制数除以2,得到余数和商,将得到的商再除以2,依次类推,直到商等于0为止,倒取除得的余数,即为所求的二进制数。例如,把52换算成二进制数的计算过程如下图:
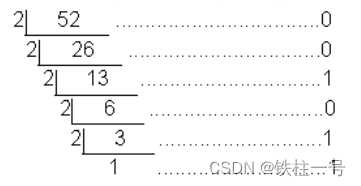
52除以2得到的余数依次为0,0,1,0,1,1,倒序排列,得到52对应的二进制数110100。
用递归的思想来描述上述计算过程是这样的:输出n/2对应的二进制数,然后输入%2。递归函数的实现过程如下:
void convert(int n)
{
if(n > 0)
{
调用自身,输出n/2对应的二进制数;
输出n%2;
}
}
试试吧!
输入
输入一个正整数n。
输出
输出n对应的二进制数。
样例输入 Copy
52
样例输出 Copy
110100
源代码
#include<stdio.h>
void convert(int n)
{
if(n > 0)
{
convert(n/2);
printf("%d",n%2);
}
}
int main()
{
int n,i;
scanf("%d",&n);
convert(n);
return 0;
}