题目:快乐数
描述:
编写一个算法来判断一个数 n 是不是快乐数。
「快乐数」 定义为:
对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和。
然后重复这个过程直到这个数变为 1,也可能是 无限循环 但始终变不到 1。
如果这个过程 结果为 1,那么这个数就是快乐数。
如果 n 是 快乐数 就返回 true ;不是,则返回 false 。
示例 1:
输入:n = 19
输出:true
解释:
12 + 92 = 82
82 + 22 = 68
62 + 82 = 100
12 + 02 + 02 = 1
leetcode链接
方法一:哈希表
由题目可知我们判断一个数字是不是快乐数,通过不断循环模拟,最后判断该数字是不是等于1,我们发现如果这个数字是快乐数,那么只需要对其进行简单的模拟即可,但是如果不是快乐数的情况呢?
对于不是快乐数的数字,我们可以分两种情况:
1.一直循环,但是不等于1
2.不循环,并且越来越大
对于第一种情况,我们可以利用哈希表来进行判断循环的操作,如果数字出现了重复,那么就是发生了循环,返回false
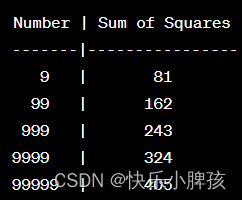
而对于第二种情况,我们发现对于不同位数的数字,其各位平方相加之和的最大值如下图所示:
以此类推,我们发现从三位数开始往后,其各位平方相加之和不可能大于这个数,所以我们对于任意一个数字,最后都不会变得无穷大,因此不存在出现第二种情况,所以对于一个不是快乐数的数字,一定会出现循环。而我们 跳出循环的方法可以利用哈希表来进行操作。
时间复杂度:o(logn) 一个值为n的数的位数为logn,因此我们查找下一个给数的时间为o(logn)
空间复杂度:o(1)
bool isHappy(int n) {
unordered_set<int> set;
while(n!=1&&!set.count(n)){//当n不等于1并且没有陷入循环的时候继续while循环
set.insert(n);
int sum = 0;
while(n>0){
int digit = n%10;
sum+=digit*digit;
n/=10;
}
n = sum;//更新n
}
return n==1;
}
方法二:快慢指针
同样的,我们出来可以利用哈希表来判断循环,还可以用快慢指针来判断循环,因为在一个循环中,快指针一定会追上慢指针,所以当我们快指针追上了慢指针时,就证明出现了循环,返回false,当没有循环的时候,快指针会比慢指针更加快的达到1,因此我们while循环的结束条件为快指针追上了慢指针或者快指针达到了1.
时间复杂度:o(logn) 同样的查找下一个数的时间为logn
空间复杂度:o(1)
bool isHappy(int n) {
int slow = n,fast = n;
do{
fast = getNext(getNext(fast));//快指针一次前进2格
slow = getNext(slow);//慢指针一次前进1格
}while(fast!=slow&&fast!=1);
return fast==1;
}
//求数字n的下一个数字
int getNext(int n){
int sum = 0;
while(n>0){
int digit = n%10;
sum+=digit*digit;
n/=10;
}
return sum;
}