---

前言

1、跳跃游戏
2、跳跃游戏||
3、K次取反后最大化的数组和

---

一、跳跃游戏（力扣55）

给定一个非负整数数组 nums ，你最初位于数组的 第一个下标 。

数组中的每个元素代表你在该位置可以跳跃的最大长度。

判断你是否能够到达最后一个下标。

思路：
这道题目关键点在于：不用拘泥于每次究竟跳几步，而是看覆盖范围，覆盖范围内一定是可以跳过来的，不用管是怎么跳的。
那么这个问题就转化为跳跃覆盖范围究竟可不可以覆盖到终点！

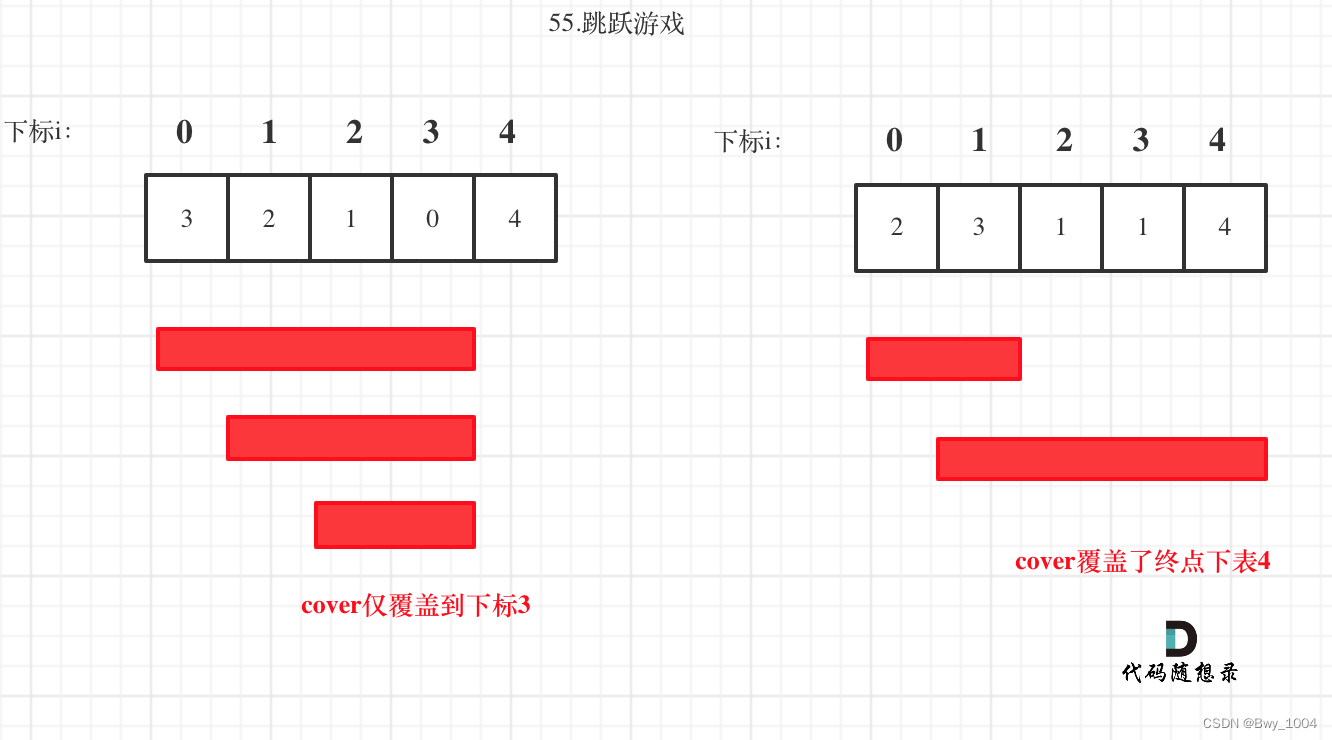
i每次移动只能在cover的范围内移动，每移动一个元素，cover得到该元素数值（新的覆盖范围）的补充，让i继续移动下去。

而cover每次只取 max(该元素数值补充后的范围, cover本身范围)。

如果cover大于等于了终点下标，直接return true就可以了。

class Solution {
    public boolean canJump(int[] nums) {
        int cover =0;
        if(nums.length==1){
            return true;
            
        }
        if(nums[0]==0) return false;
        for(int i=0;i<=cover;i++){
            int count = i+nums[i];
            cover = Math.max(cover,count);
            if(cover>=nums.length-1){
                return true;
            }
        }
        return false;
    }
}

二、跳跃游戏 II（力扣45）

给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。

每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说，如果你在 nums[i] 处，你可以跳转到任意 nums[i + j] 处:

0 <= j <= nums[i]
i + j < n
返回到达 nums[n - 1] 的最小跳跃次数。生成的测试用例可以到达 nums[n - 1]。

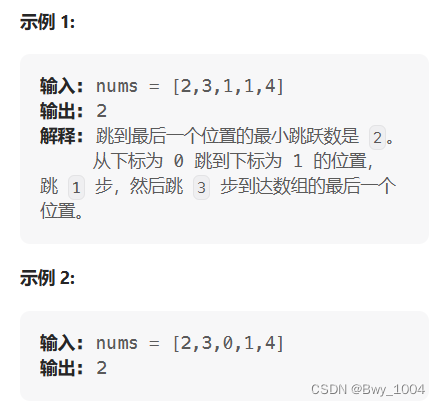
思路：
本题相对于55.跳跃游戏还是难了不少。
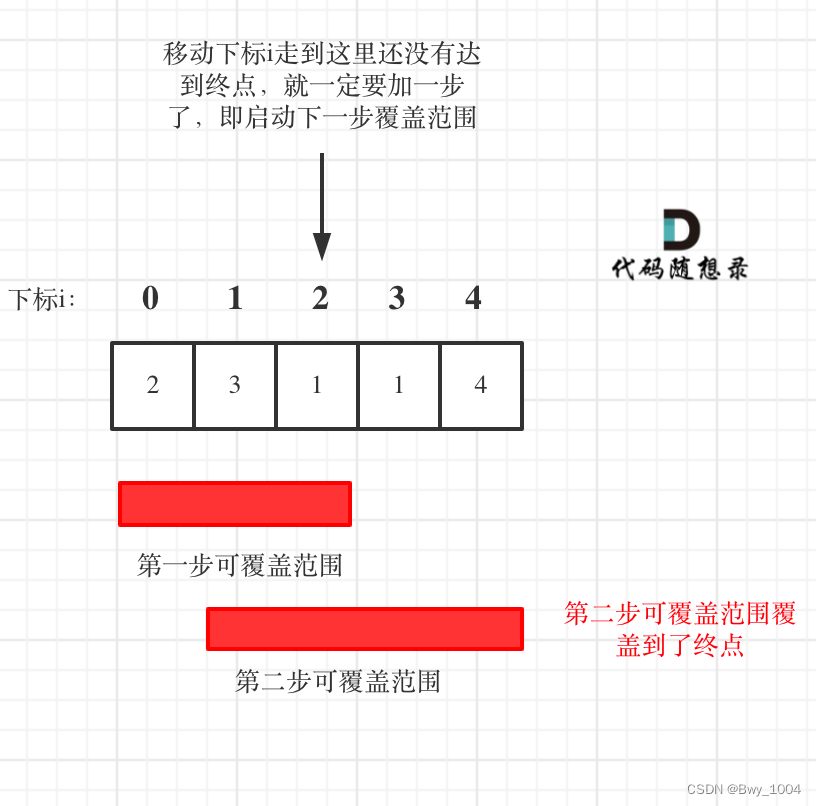
关键是思考什么时候将步数 +1。假设跳的每一个台阶都是最优的（初始是在第 0 个台阶上），那么下一次选择在哪里跳的范围是在当前台阶上可以跳的全部范围 [i+1, i + nums[i]]。也就是说要在这一个范围内贪心的选一个能到达最远的台阶。

class Solution {
    public int jump(int[] nums) {
        int res = 0;
        if(nums.length==1||nums.length==0||nums==null)
            return res;
        int curDistance = 0;//当前覆盖的最大区域
        int maxDistance = 0;//最大的覆盖区域
        for(int i=0;i<nums.length;i++){
            int count = i+nums[i];
            maxDistance = Math.max(count,maxDistance);
            if(maxDistance>=nums.length-1){
                res++;
                break;
            }
            if(i==curDistance){
                res++;
                curDistance=maxDistance;
            }
        }
        return res;
    }
}

三、K次取反后最大化的数组和（力扣1005）

给你一个整数数组 nums 和一个整数 k ，按以下方法修改该数组：

选择某个下标 i 并将 nums[i] 替换为 -nums[i] 。
重复这个过程恰好 k 次。可以多次选择同一个下标 i 。

以这种方式修改数组后，返回数组 可能的最大和 。

思路：
贪心的思路，局部最优：让绝对值大的负数变为正数，当前数值达到最大，整体最优：整个数组和达到最大。

局部最优可以推出全局最优。

那么如果将负数都转变为正数了，K依然大于0，此时的问题是一个有序正整数序列，如何转变K次正负，让 数组和 达到最大。

那么又是一个贪心：局部最优：只找数值最小的正整数进行反转，当前数值可以达到最大（例如正整数数组{5, 3, 1}，反转1 得到-1 比 反转5得到的-5 大多了），全局最优：整个 数组和 达到最大

class Solution {
    public int largestSumAfterKNegations(int[] nums, int k) {
        Arrays.sort(nums);
        for(int i=k;i>0;i--){
            nums[0]=-1*nums[0];
            Arrays.sort(nums);
        }
        int res =0;
        for(int i=0;i<nums.length;i++){
            res += nums[i];
        }
        return res;
    }
}

这个解法时间复杂度有点高，因为执行了k次快排
题解的解法：

class Solution {
    public int largestSumAfterKNegations(int[] nums, int k) {
        if(nums.length==1) return k%2==0?nums[0]:-nums[0];
        Arrays.sort(nums);
        int sum =0;
        int idx = 0;
        for(int i=0;i<k;i++){
            if(i<nums.length-1 && nums[idx]<0){
                nums[idx]=-nums[idx];
                if(nums[idx]>=Math.abs(nums[idx+1]))
                    idx++;
                continue;
            }
            nums[idx]=-nums[idx];
        }
        for(int i=0;i<nums.length;i++){
            sum+=nums[i];
        }
        return sum;
    }
}

---