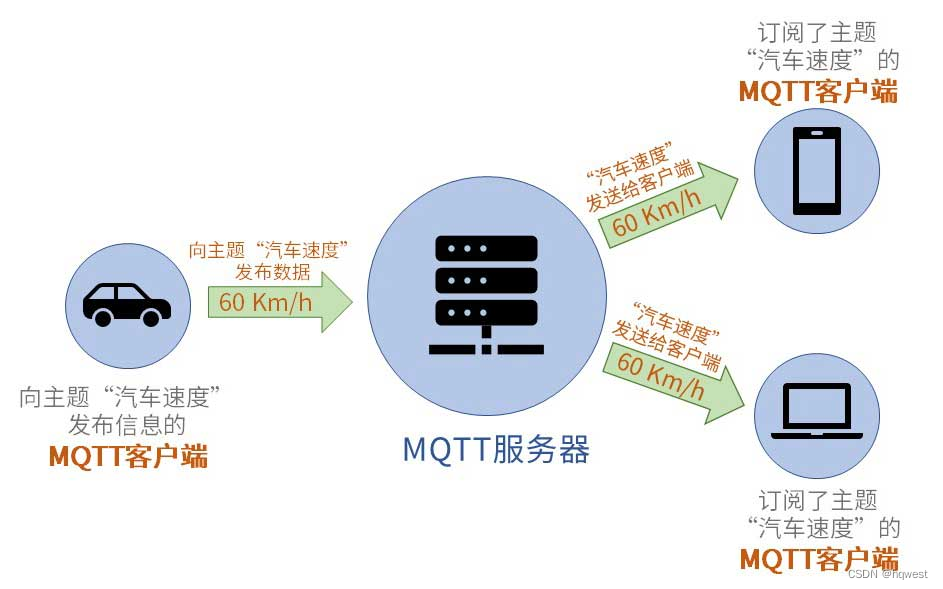
文章目录
- FEB
- 题目描述
- 输入格式
- 输出格式
- 数据范围
- 输入样例1:
- 输出样例1:
- 输入样例2:
- 输出样例2:
- 输入样例3:
- 输出样例3:
- 代码
- 题解
- 情况1:xxxxxx:0,1,2,…,k-1
- 情况2:0xxxxxx:0,1,2,…,k
- 情况3:0xxxxxx0:k+1,k-1,k-3,k-5,…
- 讨论中间的值能否都取到:
- 情况4:k,k-2,k-4,…
- 等差数列的合并
- 中间(情况3、4)的等差数列(公差为2)的合并
- 边(情况2)与边(情况2)的等差数列(公差为1)合并
- 边(情况2:公差为1)和中间(情况3,4:公差为2)的等差数列合并
FEB
题目描述
有一个长度为 N的字符串 S,其中的每个字符要么是 B,要么是 E。
我们规定 S的价值等于其中包含的子串 BB 以及子串 EE 的数量之和。
例如,BBBEEE 中包含 2个 BB 以及 2个 EE,所以 BBBEEE 的价值等于 4。
我们想要计算 S的价值,不幸的是,在我们得到 S之前,约翰将其中的一些字符改为了 F。
目前,我们只能看到改动后的字符串 S,对于其中的每个 F,我们并不清楚它之前是 B 还是 E。
请你计算,改动前的 S有多少种可能的价值并将所有可能价值全部输出。
输入格式
第一行包含一个整数 N。
第二行包含改动后的字符串 S。
输出格式
第一行输出一个整数 K,表示改动前的 S的可能价值的数量。
接下来 K 行,按照升序顺序,每行输出一个可能价值。
数据范围
1≤N≤2×105
输入样例1:
4
BEEF
输出样例1:
2
1
2
输入样例2:
9
FEBFEBFEB
输出样例2:
2
2
3
输入样例3:
10
BFFFFFEBFE
输出样例3:
3
2
4
6
代码
#include<bits/stdc++.h>
using namespace std;
int n; // 声明一个整型变量n来存储字符串的长度
string s; // 声明一个字符串变量s来存储输入的字符串
int main() {
cin >> n >> s; // 从标准输入读取字符串的长度n和字符串s
// 情况一:如果字符串s完全由字符'F'组成
if(s == string(n, 'F')) {
cout << n << endl; // 输出n,可能的价值数量为字符串长度
for(int i = 0; i < n; i++)
cout << i << endl; // 按顺序输出从0到n-1的整数
}
else {
int l = 0, r = n - 1;
// 跳过字符串s左边的'F'字符
while(s[l] == 'F') l++;
// 跳过字符串s右边的'F'字符
while(s[r] == 'F') r--;
int min = 0, max = 0; // 初始化最小和最大价值为0
auto str = s;
// 估算最小价值
for(int i = l; i <= r; i++) {
if(str[i] == 'F') {
// 如果F的前一个字符是B,则假设F是E,反之亦然
if(str[i - 1] == 'B') str[i] = 'E';
else str[i] = 'B';
}
// 计算相邻字符相同的情况,增加最小价值
if(i > l && str[i] == str[i - 1]) min++;
}
str = s;
// 估算最大价值
for(int i = l; i <= r; i++) {
// 将F替换为它前面的字符(B或E)
if(str[i] == 'F') str[i] = str[i - 1];
// 计算相邻字符相同的情况,增加最大价值
if(i > l && str[i] == str[i - 1]) max++;
}
//计算左右两边的最大价值
//左边:0~l-1,共l-1-0+1=l个数,例:0~4-1,0,1,2,3共4个数,4-1+1
//右边:r+1~n-1 共n-1-(r+1)+1=n-1-r个数
int ends = l + n - 1 - r, d = 2;
// 调整最大价值,并确定输出价值的间隔
if(ends) max += ends, d = 1;//如果ends不为0,说明公差为1和公差为1的等差数列合并,公差为1,反之,ends为0,说明两边没有F段,公差为2
//并求总等差数列的最大值,最小值不变,因为两边的等差数列最小值=0
cout << (max - min) / d + 1 << endl; // 输出总的价值数量
for(int i = min; i <= max; i += d)
cout << i << endl; // 逐个输出每个可能的价值
}
return 0;
}
题解
第一步,先分析每一段连续的x的价值有哪些种。
第二步,再分析所有段的价值之和有哪些。
k在下面表示x的数量
情况1:xxxxxx:0,1,2,…,k-1

情况2:0xxxxxx:0,1,2,…,k

情况3:0xxxxxx0:k+1,k-1,k-3,k-5,…
最大值:k+1
最小值:
- k为偶数:min=1
- k为奇数,min=0
讨论中间的值能否都取到:
任何一个方案都可以通过全0的方案变换过来
全0的方案,最大值为k+1
变了中间任意一个数(每改变一位),在原有的基础上±两个1,k+1±1±1
新价值=原价值±1±1,奇偶性一样
所以,所有的情况是:k+1,k-1,k-3,k-5,…
如果k=5,max=6,6-2=4,4-2=2,2-2=0;
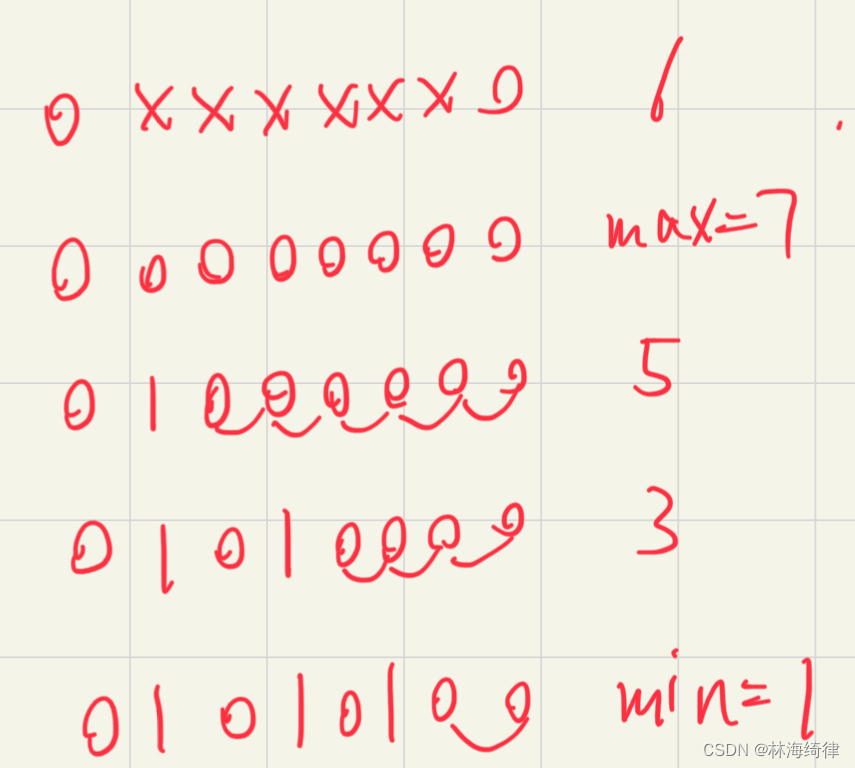
情况4:k,k-2,k-4,…

最大值:k
最小值:
- k为偶数:0
- k为奇数:1
等差数列的合并
中间(情况3、4)的等差数列(公差为2)的合并
合并两个公差为2的等差数列,仍然会得到一个公差为2的等差数列,最小值为两个等差数列最小值相加,最大值为两个等差数列最大值相加,中间所有公差为2的数都取得到。
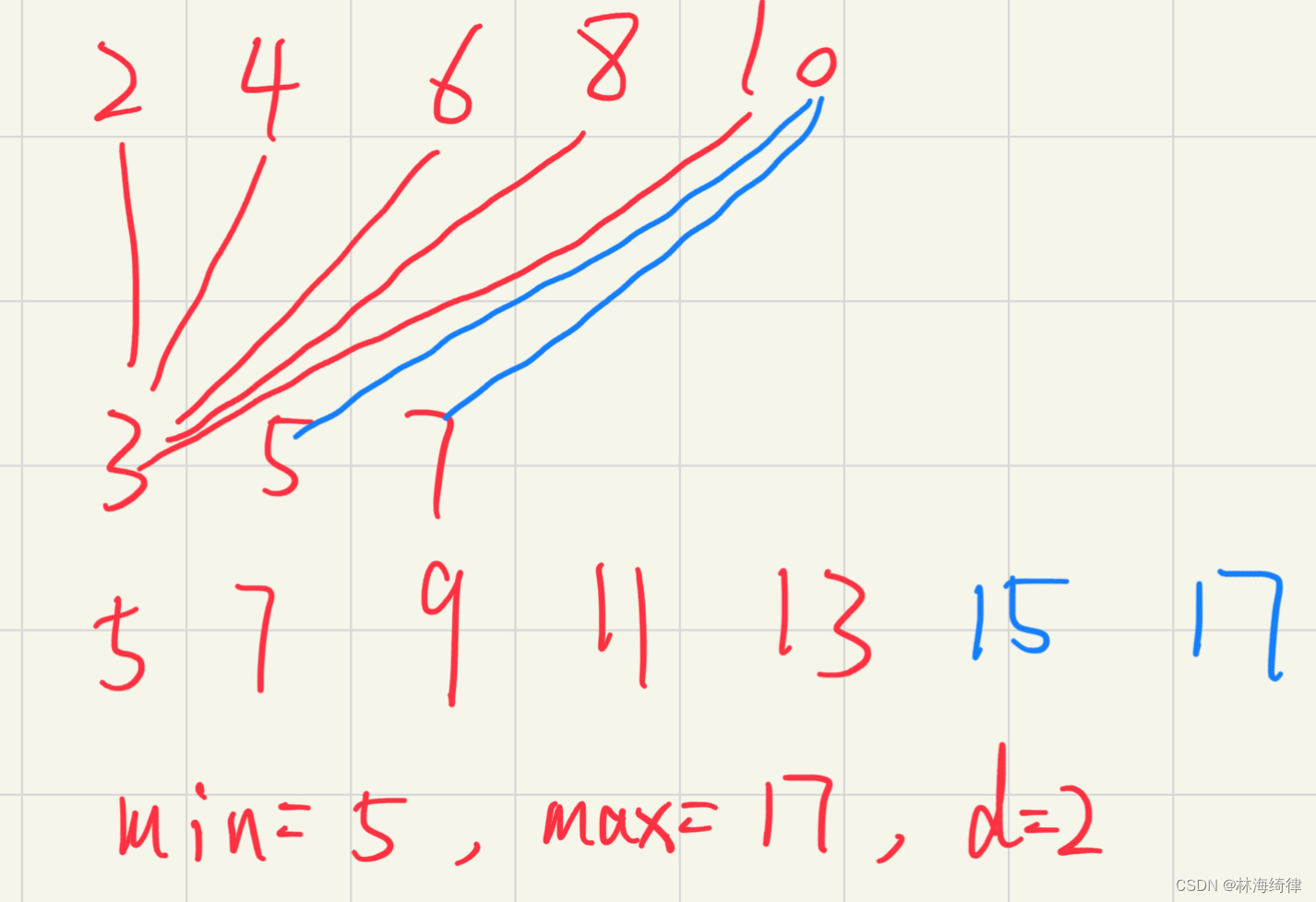
总价值数量为(17-5)/2+1=7
总价值数量公式:(max-min)/d+1
边(情况2)与边(情况2)的等差数列(公差为1)合并
合并一个公差为1的等差数列,得到一个公差为1的等差数列,最小值为两个等差数列最小值相加,最大值为两个等差数列最大值相加,中间所有公差为1的数都取得到。
边(情况2:公差为1)和中间(情况3,4:公差为2)的等差数列合并
合并一个公差为2的等差数列和公差为1的等差数列,得到一个公差为1的等差数列,最小值为两个等差数列最小值相加,最大值为两个等差数列最大值相加,中间所有公差为1的数都取得到。
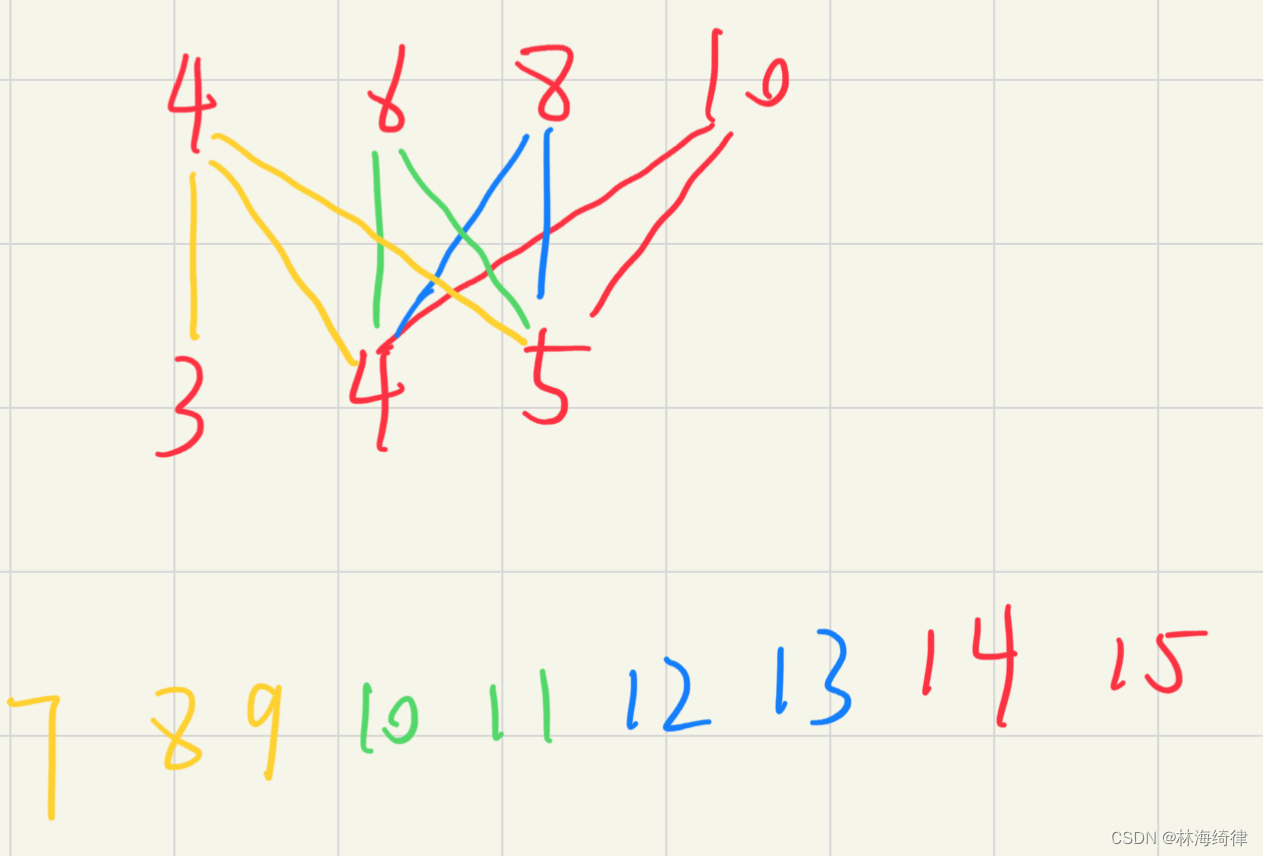
总价值数量为(15-7)/1+1=9
总价值数量公式:(max-min)/d+1