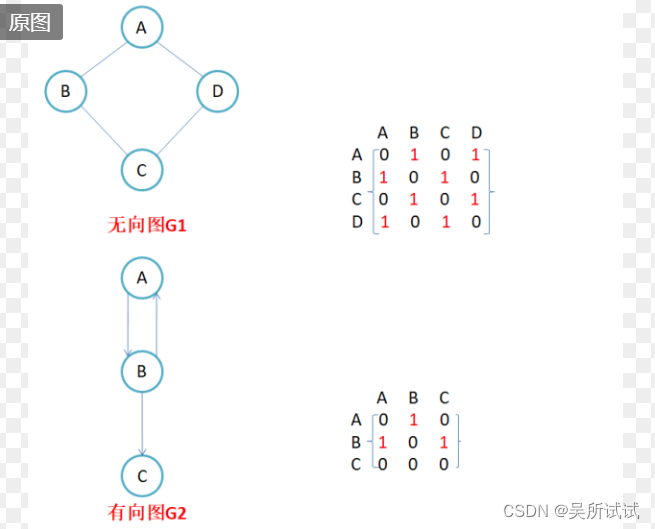
【一】图的基本概念
图是由顶点集合和顶点之间的关系组成的一部分:G=(V,E),其中:
顶点集合V = {x|x属于某个数据对象集}是有穷非空集合;
E = {(x,y)|x,y
属于
V}
或者
E = {<x, y>|x,y
属于
V && Path(x, y)}
是顶点间关系的有穷集合,也叫做边的集
合
。
(x, y)
表示
x
到
y
的一条双向通路,即
(x, y)
是无方向的;
Path<x, y>
表示从
x
到
y
的一条单向通路,即
Path<x, y>
是有方向的。
顶点和边:
图中结点称为顶点
,第
i
个顶点记作
vi
。
两个顶点
vi
和
vj
相关联称作顶点
vi
和顶点
vj
之间有一条边
,
图中的第
k
条边记作
ek
,
ek = (vi
,
vj)
或
<vi
,
vj>
。
有向图和无向图:
在有向图中,顶点对
<x, y>
是有序的,顶点对
<x
,
y>
称为顶点
x
到顶点
y
的一条边
(
弧
)
,
<x,
y>
和
<y, x>
是两条不同的边
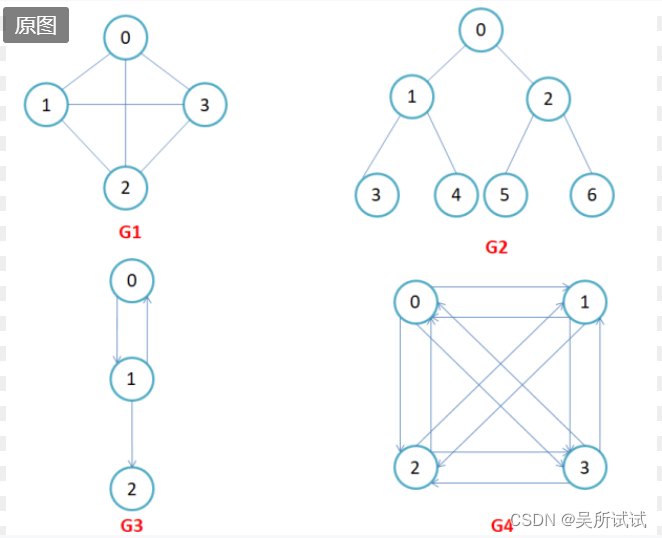
,比如下图
G3
和
G4
为有向图。在
无向图中,顶点对
(x, y)
是无序的,顶点对
(x,y)
称为顶点
x
和顶点
y
相关联的一条边,这条边没有特定方向,
(x, y)
和
(y
,
x)
是同一条边
,比如下图
G1
和
G2
为
无向图。注意:
无向边
(x, y)
等于有向边
<x, y>
和
<y, x>
。
完全图:在
有
n
个顶点的无向图中
,若
有
n * (n-1)/2
条边
,即
任意两个顶点之间有且仅有一条边
,则称此图为
无向完全图
,比如上图
G1
;在
n
个顶点的有向图
中,若
有
n * (n-1)
条边
,即
任意两个顶点之间有且仅有方向
相反的边
,则称此图为
有向完全图
,比如上图
G4
。
出度之和
,其中顶点
v
的
入度是以
v
为终点的有向边的条数
,记作
indev(v);
顶点
v
的
出度是以
v
为起始点的有向
边的条数
,记作
outdev(v)
。因此:
dev(v) = indev(v) + outdev(v)
。注意:对于
无向图,顶点的度等于该顶
点的入度和出度
,即
dev(v) = indev(v) = outdev(v)
。
路径:在图
G = (V
,
E)
中,若
从顶点
vi
出发有一组边使其可到达顶点
vj
,则称顶点
vi
到顶点
vj
的顶点序列为从
顶点
vi
到顶点
vj
的路径
。
路径长度:对于
不带权的图,一条路径的路径长度是指该路径上的边的条数
;对于
带权的图,一条路径的路
径长度是指该路径上各个边权值的总和
。
tips:有向完全图只是单纯的在无相完全图上面的每一条边上加上一个相反的边而已,所以求解的时候乘以2或者除以2即可。
联通图:在无向图中,若从顶点v1到顶点v2有路径,则顶点v1和顶点v2是联通的,如果图中任意一对顶点都是联通的,则这个图就是连通图。
强连通图:在有向图中任何一对顶点都是互相联通的,那么称此图为强联通图。
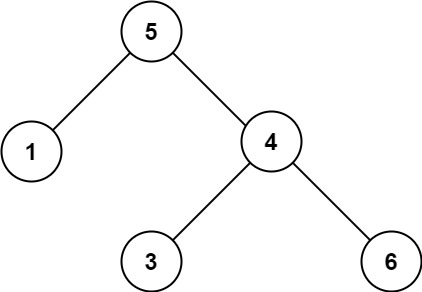
生成树:一个连通图的最小连通子图称为该图的生成子树,有n个顶点的连通图的生成树有n个顶点和n-1条边。
【二】图的存储结构
因为图中既有节点,又有边(节点与节点之间的关系),因此,在图的存储中,只需要保存:节点和边的关系即可。节点保存比较简单,只需要一段连续的空间即可,那边关系怎么保存呢?那就涉及到一个叫临接矩阵的概念了。
邻接矩阵:因为节点和节点之间的关系就是联通与否,即为0或者1,因此邻接矩阵(二维数组)即是:先用一个数组将定点保存,然后采用矩阵表示节点和节点之间的关系。
1.无向图的邻接举证是对称的,第i行(列)元素之和就是顶点的度,有向图的临接矩阵则不一定是对称的,第i行(列)元素之后就是顶点的i的出(入)度。
2.如果边带有权值,并且两个节点之间是联通的,上图中的边的关系就使用权值代替,如果两个顶点不通,就使用无穷大代替。
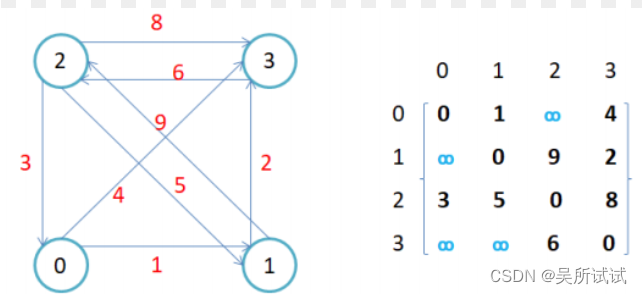
使用邻接矩阵存储图的优点就是能过去快速的知道这两个顶点是否连通,缺陷是如果顶点比较多,边比较少时,矩阵中存储了大量的0成为系数矩阵,比较浪费空间,并且要求两个节点之间的路径不是很好求。
邻接表:使用数组表示顶点的集合,使用链表表示边的关系
1.无相图邻接表存储
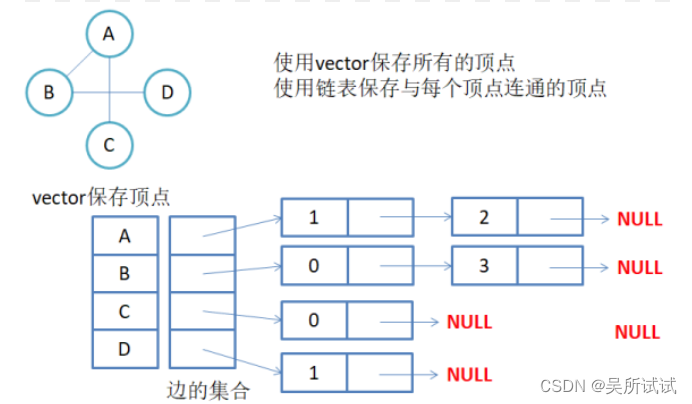
注意:无向图中,同一条边在邻接表中出现了两次,如果想知道顶点vi的度,只需要知道顶点vi边链表集合中节点的数目即可。
有向图的邻接表存储:
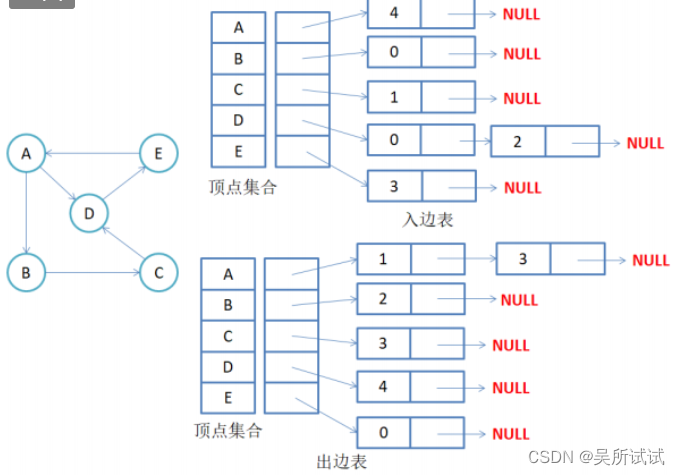
注意:有向图中每条边在邻接表中只出现一次,与顶点vi对应的邻接表所含节点的个数,就是该节点的出度,但是如果你想要找到节点的入度,你必须去检查所有顶点对应的边链表,看看有多少顶点的目的值是i。
【三】图的遍历:
给定一个图G和任意一个顶点v0,从v0出发,沿着图中各边访问图中的所有顶点,且每个顶点仅被遍历一遍,遍历就是对个个顶点进行操作的意思。
广度和深度优先遍历:
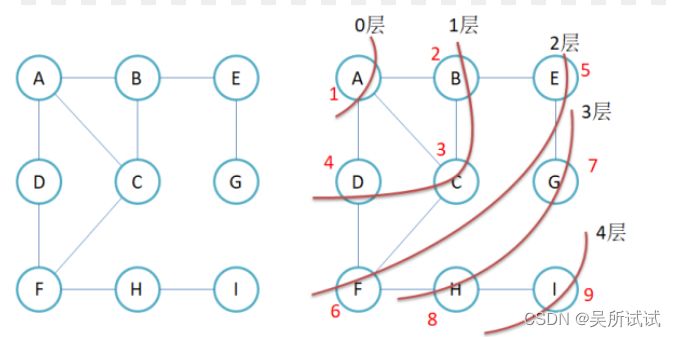
广度优先遍历:
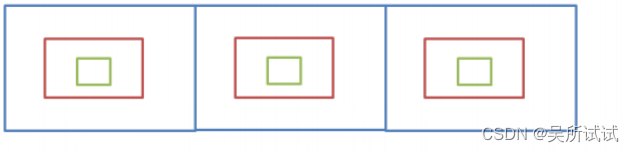
比如现在要找东西,假设有三个抽屉,东西在哪个抽屉我们是不清楚的。
广度优先遍历的做法是: 打开蓝色盒子之后看看有没有,没有的话再打开红色的盒子,依次类推,直到找到。
深度优先遍历的做法是:打开蓝色盒子之后不管有没有,直接打开红色盒子,也不管有没有,再打开绿色盒子。然后检查绿色盒子有没有,绿色盒子没有去看红色盒子,直到找到,以此类推。
【四】最小生成树
连通图的每一颗生成树,都是原图一个极大无环子图,即:从中删除任何任何一条边,生成树就不在联通,反之,再其中引入任何一条新边,都会形成一条回路。
若连通图由n个顶点,则其生成树必含n个顶点和n-1条边,因此构造最小生成树准则有三条:
1.只能使用图中的边来构造最小生成树
2.只能使用n-1条边来链接图中的n个顶点
3.选用的n-1条边不能构成回路
a.krushal算法
任给一个有n个顶点的联通网络N={V,E};
首先构造一个由这n个顶点组成、不含任何边的图G={V,NULL},其中每个顶点自成一个连通分量,然后不断从E中取出权值最小的一条边(如果相同任取其一),若该边的两个顶点来自不同的联通分量,就将这个边加入到G中,如此重复,直到所有顶点都在同一个联通分量上。如此重复,直到所有顶点再同一个联通分量上。
核心:每次迭代时,选出一条具有最小权值,且两端点不在同一联通分量上的边,加入生成树。
以上就是这期的全部内容了,如果哪里有地方理解错了,还请位于评论区斧正,如果没有问题的话,还请一键三连,毕竟码字不易。