前言

leetcode 42. 接雨水是一道业内著名的hard题，多次出现在面试场上，经久不衰，难住了一届又一届的候选人。

作为leetcode上热度最高的题目之一，题目评论区也是好一番热闹景象。有人表示看了三天做不出来，有人在评论区洋洋洒洒五六种解法。

其实在这么多的解法中，我们只需要着重掌握双指针和单调栈两种即可。

当然，暴力解法可以不屑，但不能不会。

所有的解法大致可以分为两类：按行求和按列求，所谓按“列”求，是指将雨水部分按列拆分，分别计算数组0位置，1位置，…，n-1位置的答案。

所谓按行求，是指将雨水部分按行拆分成n个部分，然后分别计算每个部分能积攒多少水，最后再将结果汇总。

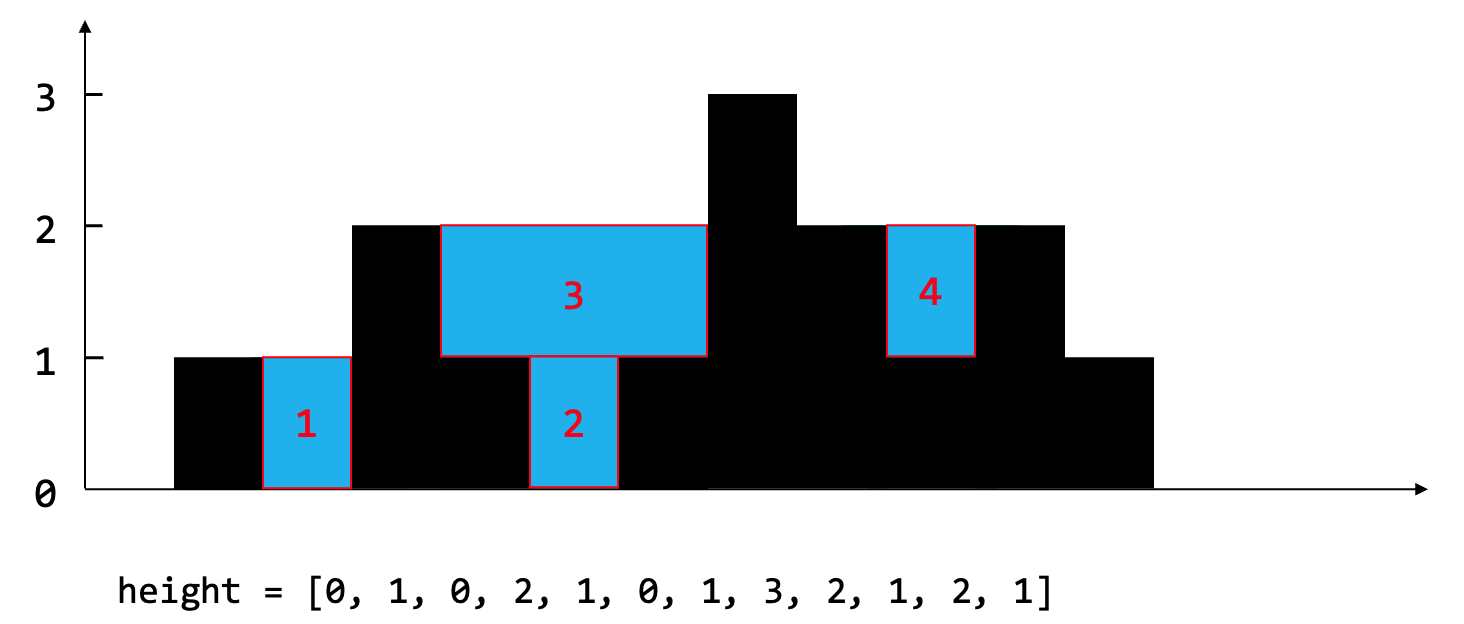
在本文给出的几种解法中，解法 1、2、3 都是按列求的，解法 4 是按行求的。

题目描述

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例 1：

输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。

示例 2：

输入：height = [4,2,0,3,2,5]
输出：9

解法一：暴力

超出时间限制，不能通过

算法思路

逐个计算每一列能存下的水量。

遍历整个数组。针对数组中的每个元素arr[i]，都分别向左、向右遍历一遍数组，找到arr[i]左侧和右侧的最大值，计为leftMax和rightMax，如果leftMax <= arr[i]或者rightMax <= arr[i]，说明当前这一列存不出水。否则当前列能存储的水量为min(leftMax, rightMax) - arr[i]。

所以数组的i位置能存储的水量res[i] = max{0, min{max(arr[0...i-1]), max(arr[i+1...n])} - arr[i] }。

再思考一下，如果max(arr[0...i-1]) > arr[i]，那么数组0到i-1位置的最大值和0到i位置的最大值一定是相等的；如果max(arr[0...i-1]) <= arr[i]，那么数组0到i位置的最大值一定等于arr[i]，所以为了避免和0之间取max的计算，上述公式可以化简为下面的形式。
r e s [ i ] = m i n { m a x { a r r [ 0... i ] } , m a x { a r r [ i . . . n − 1 ] } } − a r r [ i ] res[i] = min\{max\{arr[0...i]\}, max\{arr[i...n-1]\}\} - arr[i] res[i]=min{max{arr[0...i]},max{arr[i...n−1]}}−arr[i]

代码实现

int trap(vector<int>& height) {
	int sum = 0;
    int n = height.size();
    for (int i=0; i<n; i++) {
        int leftMax = 0;
        for (int j=0; j<=i; j++) {
            if (height[j] > leftMax) {
                leftMax = height[j];
            }
        }

        int rightMax = 0;
        for (int j=i; j<n; j++) {
            if (height[j] > rightMax) {
                rightMax = height[j];
            }
        }

        sum += min(leftMax, rightMax) - height[i];
    }

    return sum;
}

复杂度分析

• 时间复杂度：$O(n^2)$
• 空间复杂度：$O(1)$

解法二：双指针

从暴力解法中我们可以看到，要求数组i位置可以存储的水量，需要先求出0到i位置的最大值max(arr[0...i])，再求出i到n-1位置的最大值max(arr[i...n-1])，两个值中取最小与arr[i]做差。

暴力解法之所以时间复杂度比较差，是因为对于数组中的每一个元素，都需要再遍历一遍数组才能得到它左右两侧的最大值。

所以我们可以通过预处理数组得到leftMax[]和rightMax[]两个数组，leftMax[i]代表数组0到i位置的最大值，leftMax[i] = max(leftMax[i-1], arr[i])；rightMax[i]代表数组i位置到n-1位置的最大值，rightMax[i] = max(rightMax[i+1], arr[i])。

这样我们就得到了如下的算法流程。

首先遍历数组，从左向右得到数组leftMax[]，再从右向左得到rightMax[]。然后再遍历一遍数组，对于数组的每一个位置i，通过leftMax[i]，rightMax[i]和arr[i]得到结果，将结果汇总得到的值就是最终答案。

代码实现

C++

int trap(vector<int>& height) {
    int n = height.size();
    vector<int> leftMax(n, 0);
    leftMax[0] = height[0];
    for (int i=1; i<n; i++) {
        leftMax[i] = max(leftMax[i-1], height[i]);
    }

    vector<int> rightMax(n, 0);
    rightMax[n-1] = height[n-1];
    for (int i=n-2; i>=0; i--) {
        rightMax[i] = max(rightMax[i+1], height[i]);
    }

    int res = 0;
    for (int i=0; i<n; i++) {
        res += min(leftMax[i], rightMax[i]) - height[i];
    }

    return res;
}

Java

public int trap(int[] height) {
	int n = height.length;
    int[] leftMax = new int[n];
    leftMax[0] = height[0];
    for (int i=1; i<n; i++) {
        leftMax[i] = Math.max(leftMax[i-1], height[i]);
    }

    int[] rightMax = new int[n];
    rightMax[n-1] = height[n-1];
    for (int i=n-2; i>=0; i--) {
        rightMax[i] = Math.max(rightMax[i+1], height[i]);
    }

    int res = 0;
    for (int i=0; i<n; i++) {
        res += Math.min(leftMax[i], rightMax[i]) - height[i];
    }

    return res;
}

Go

func trap(height []int) int {
    n := len(height)
    leftMax := make([]int, n)
    leftMax[0] = height[0]
    for i:=1; i<n; i++ {
        leftMax[i] = max(leftMax[i-1], height[i])
    }

    rightMax := make([]int, n)
    rightMax[n-1] = height[n-1]
    for i:=n-2; i>=0; i-- {
        rightMax[i] = max(rightMax[i+1], height[i])
    }

    res := 0
    for i:=0; i<n; i++ {
        res += min(leftMax[i], rightMax[i]) - height[i]
    }
    return res
}

复杂度分析

• 时间复杂度：$O(n)$
• 空间复杂度：$O(n)$，借助了两个数组

解法三：双指针进阶

解法二中的双指针需要遍历三次数组，第一次得出数组leftMax[]，第二次得出数组rightMax[]，第三次才是根据leftMax[i]，rightMax[i]和height[i]得出结果。那我们能不能想办法把这三次遍历合并成一次呢？

我们设置两个指针，left指向数组的0位置，right指针指向数组的n-1位置。再使用两个变量leftMax和rightMax，leftMax的含义是数组0...left位置的最大值，rightMax的含义是数组right...n-1位置的最大值，这几个变量设置好后就有以下几种情况。

• leftMax < rightMax，此时可以使用leftMax来结算height[left]位置的储水量。它的右侧可能还会有比rightMax更高的元素，但不会影响left位置的储水量。因为这种情况下left位置左侧的最大值是影响该位置储水量的瓶颈，此时res[left] = leftMax - height[left]。
• leftMax > rightMax，此时可以使用rightMax来结算right位置的储水量。同样的，它的左侧可能还会有比leftMax更高的元素，但都不影响right位置的储水量。因为这种情况下right位置右侧的最大值是影响该位置储水量的瓶颈。此时res[right] = rightMax - height[right]。
• leftMax == rightMax，此时既可以结算左侧，也可以结算右侧，或者左右两侧可以同时结算储水量。res[left] = leftMax - height[left]，res[right] = rightMax - height[right]。但是要注意如果结算前left == right，此时只能结算一侧。

不断重复上述流程，哪侧结算就将哪侧的指针相应移动，并在移动的过程中更新leftMax和rightMax，直到两个指针会合，结算完最后一个位置的水量为止。

以题目中的示例1为例，height = [0, 1, 0, 2, 1, 0, 1, 3, 2, 1, 2, 1]。初始状态left指针指向0位置，right指针指向n-1位置，leftMax = height[0] = 0，rightMax = height[n-1] = 1。

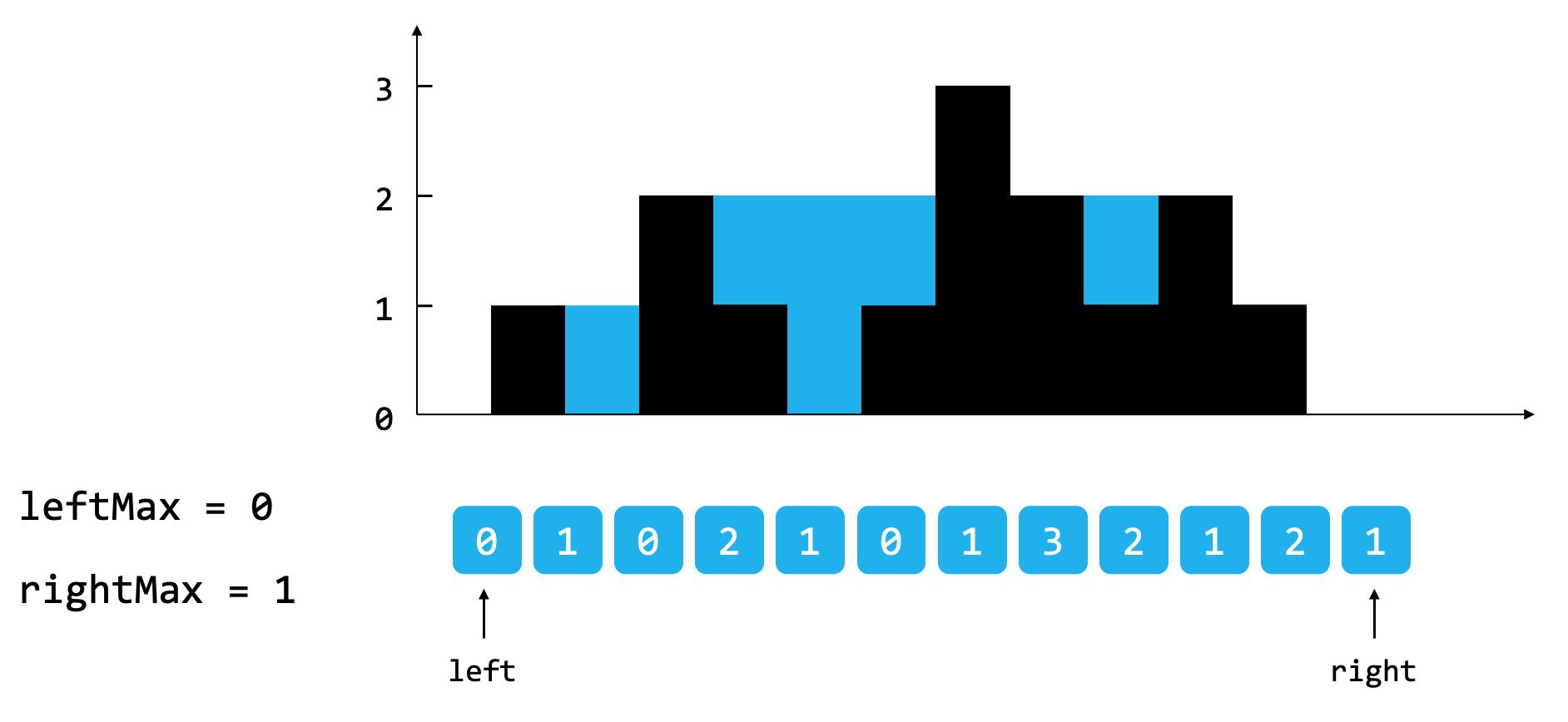
此时leftMax < rightMax，所以可以结算left位置的水量，res[0] = leftMax - height[0] = 0 - 0 = 0，计算后left指针向右偏移一位，leftMax更新为1。

此时，leftMax == rightMax，我们既可以结算左侧，也可以结算右侧，也可以双侧结算。我们这里采用双侧结算的方式，首先计算左侧水量res[1] = leftMax - height[1] = 1 - 1 = 0，left指针向右偏移；然后计算右侧水量res[11] = rightMax - height[11] = 1 - 1 = 0，right指针向左偏移，同时更新rightMax变量。

此时，leftMax < rightMax，结算左侧水量。res[2] = leftMax - height[2] = 1 - 0 = 1，left指针向右偏移一位，同时更新leftMax。

此时，leftMax == rightMax，双侧结算。res[3] = leftMax - height[3] = 2 - 2 = 0，left指针向右偏移；res[10] = rightMax - height[10] = 2 - 2 = 0，right指针向左偏移。

此时leftMax和rightMax依然相等，所以双侧结算。res[4] = leftMax - height[4] = 2 - 1 = 1，res[9] = rightMax - height[9] = 2 - 1 = 1。left指针向左偏移，right指针向右偏移。

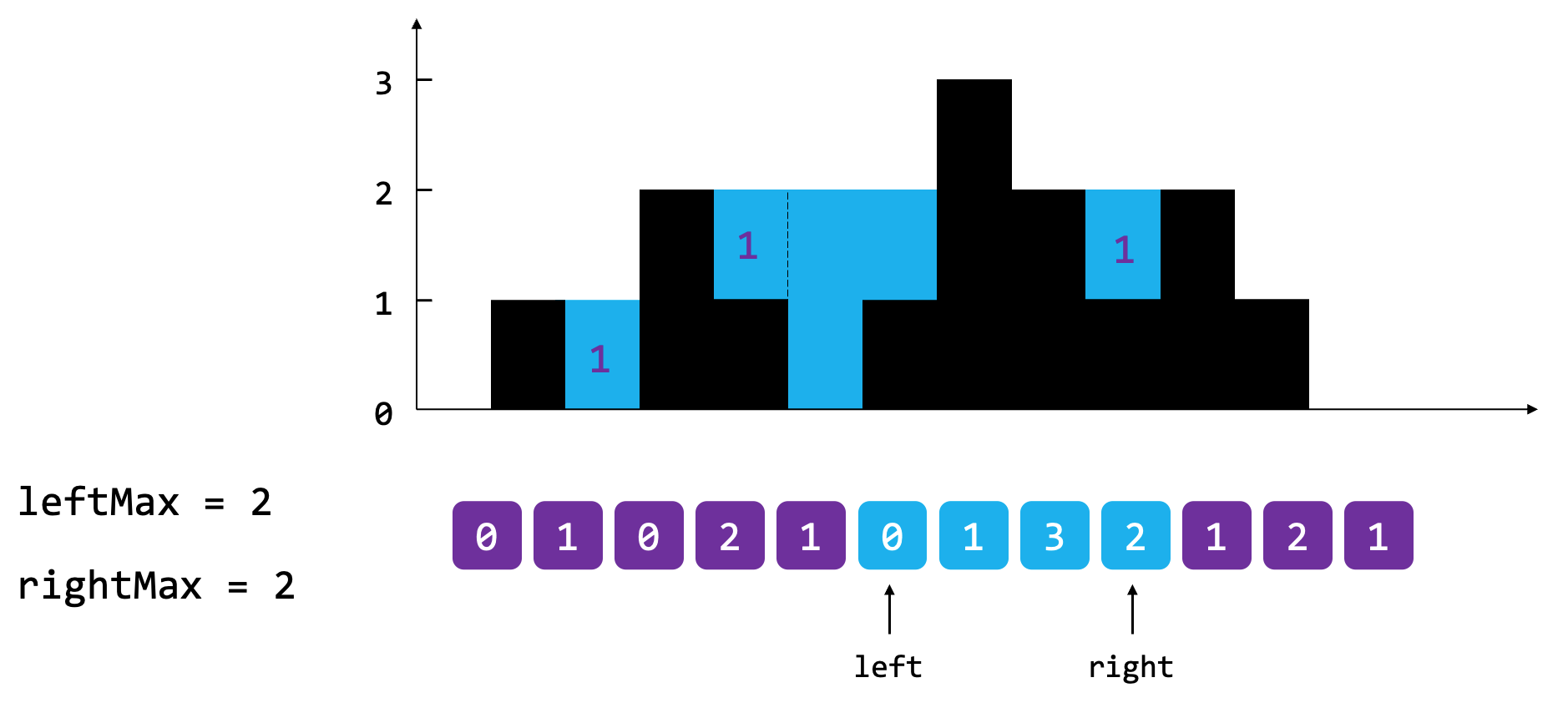
此时leftMax与rightMax依然相等，所以双侧结算。res[5] = leftMax - hegiht[5] = 2 - 0 = 2，left指针向右偏移；res[8] = rightMax - height[8] = 2 - 2 = 0，right指针向左偏移，rightMax变量同步更新为3。

此时，leftMax < rightMax，所以左侧结算，res[6] = leftMax - height[6] = 2 - 1 = 1，left指针右移，leftMax同步更新为3。

注意，此时leftMax和rightMax相等，所以双侧结算。首先结算左侧，res[7] = leftMax - height[7] = 3 - 3 = 0，left指针偏移。left指针偏移之后，就不再满足left <= right的条件了，证明流程应该终止，所以不再结算右侧，流程结束。

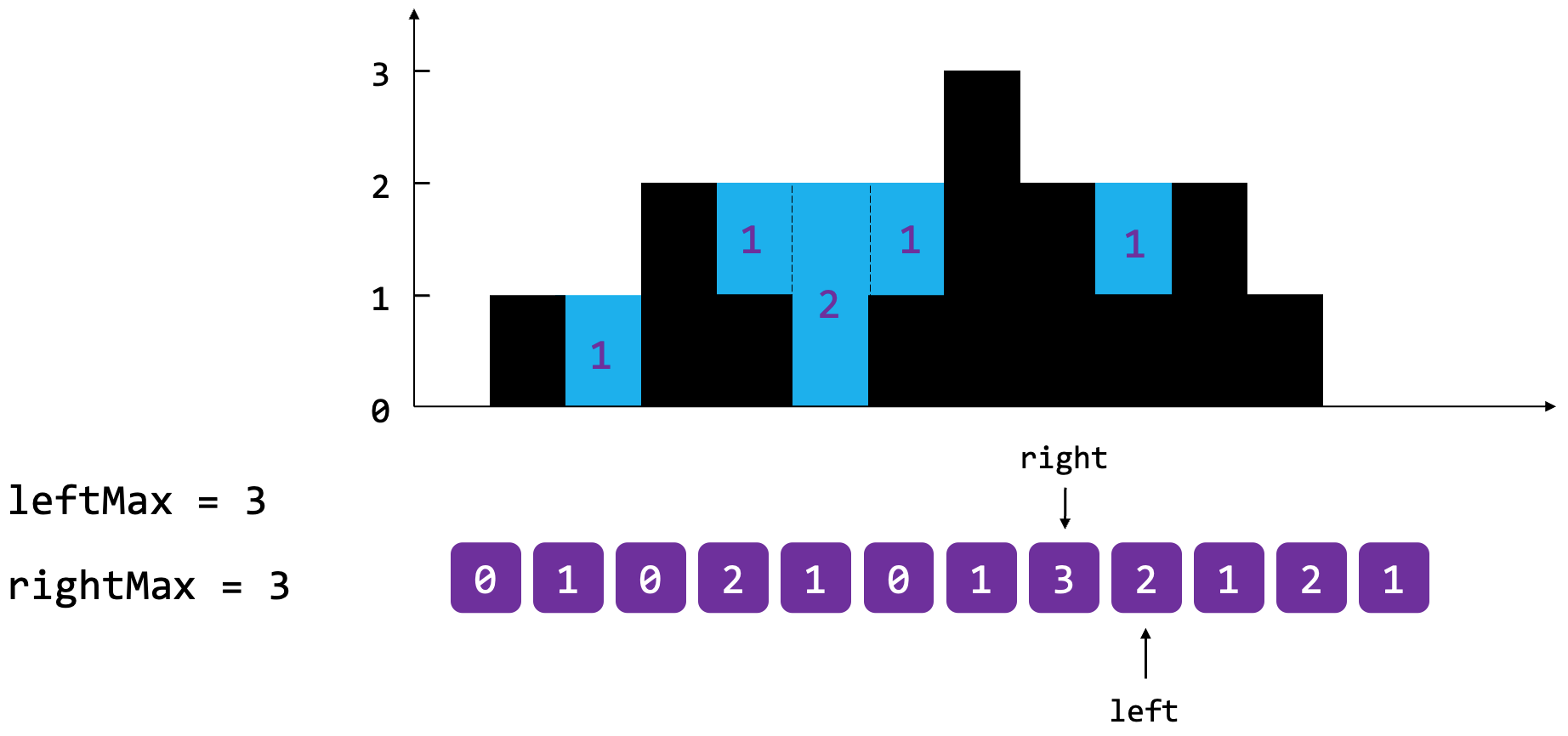
至此，整个求解流程就结束了。题目要求的结果，就是数组各个位置求得答案的汇总，即0 + 0 + 1 + 0 + 1 + 2 + 1 + 0 + 0 + 1 + 0 + 0 = 6。

代码实现

C++

int trap(vector<int>& height) {
    int n = height.size();
    int leftMax = 0, rightMax = 0, left = 0, right = n-1, res = 0;

    while (left <= right) {
        leftMax = max(leftMax, height[left]);
        rightMax = max(rightMax, height[right]);

        if (leftMax < rightMax) {
            // 左侧结算
            res += leftMax - height[left++];
        } else if (leftMax > rightMax) {
            // 右侧结算
            res += rightMax - height[right--];
        } else {
            // 双侧结算
            res += leftMax - height[left++];
            if (left <= right) {
                res += rightMax - height[right--];
            }
        }
    }
    return res;
}

Java

public int trap(int[] height) {
    int n = height.length;
    int leftMax = 0, rightMax = 0, left = 0, right = n - 1, res = 0;
    while (left <= right) {
        leftMax = Math.max(leftMax, height[left]);
        rightMax = Math.max(rightMax, height[right]);

        if (leftMax < rightMax) {
            // 左侧结算
            res += leftMax - height[left++];
        } else if (leftMax > rightMax) {
            // 右侧结算
            res += rightMax - height[right--];
        } else {
            // 双侧结算
            res += leftMax - height[left++];
            if (left <= right) {
                res += rightMax - height[right--];
            }
        }
    }
    return res;
}

Go

func trap(height []int) int {
    n := len(height)
    leftMax, rightMax, left, right, res := 0, 0, 0, n-1, 0

    for left <= right {
        leftMax = max(leftMax, height[left])
        rightMax = max(rightMax, height[right])

        if leftMax < rightMax {
            res += leftMax - height[left]
            left++
        } else if leftMax > rightMax {
            res += rightMax - height[right]
            right--
        } else {
            res += leftMax - height[left]
            left++
            if left <= right {
                res += rightMax - height[right]
                right--
            }
        }
    }

    return res
}

复杂度分析

• 时间复杂度：$O(n)$
• 空间复杂度：$O(1)$

解法四：单调栈

算法思路

到目前为止，我们已经得到了时间复杂度为$O(n)$，空间复杂度$O(1)$的解法。再想一下，什么时候能存住雨水呢？一定是左右两侧都有大于元素存在。那如何求解左右两侧的大于元素呢？单调栈！

算法流程是这样的。设置一个单调栈，栈底到栈顶元素单调递减。遍历数组，将遍历的元素arr[i]准备放入单调栈，此时有以下三种情况。(假设栈顶元素为stack[top])

• 栈中元素为空或arr[i] < stack[top]，此时arr[i]放入栈中不会破坏单调栈结构，直接放入。
• arr[i] > stack[top]，此时的arr[i]如果放入栈中，会破坏单调栈结构。此时将栈顶元素弹出，如果栈不为空，说明弹出的栈顶元素左侧有大于元素（就是此时弹栈后的栈顶元素），右侧也有大于元素（就是arr[i]），说明这里存在积水，可以结算积水的量。
  • 积水的高等于arr[i]和弹栈之后的栈顶元素中的最小值 减去 弹出元素的值
  • 用一个变量index代表弹栈之后的栈顶元素在数组中的索引值，那么积水的宽等于i - index - 1
  • 两者相乘即为此处的积水量
• arr[i] == stack[top]，此时arr[i]既可以直接入栈，也可以弹出栈顶元素并结算积水量。为什么会这样呢？大家往下看。

我们给出一个示例：height = [4, 2, 2, 1, 3]，它代表的柱状图如下所示，根据图片我们可以知道，这个示例的储水量等于4。

根据上面描述的算法流程，首先准备将数组0位置的4放入单调栈。初始状态栈为空，0位置的4放入不会破坏单调栈结构，所以可以直接放入。

1位置的2入栈也不会破坏单调栈结构，所以也直接入栈。

接下来是2位置的2，栈顶元素也是2，命中了第三种情况，我们先让元素直接入栈。3位置的1也可以直接入栈。

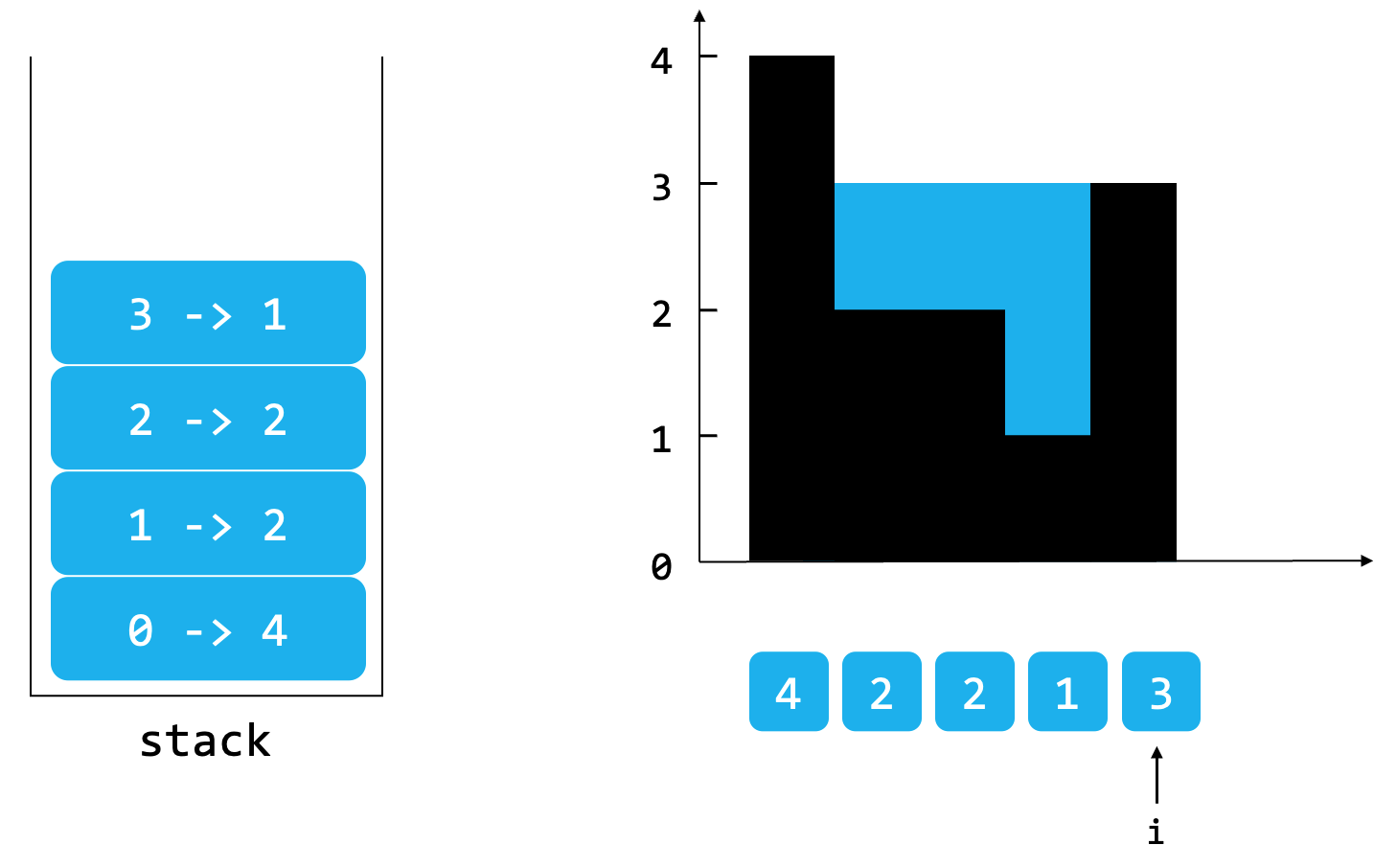
接下来遍历到数组4位置的3，它大于现在的栈顶元素，不能直接入栈。所以将栈顶元素弹出。

栈顶元素弹出后，栈不为空，说明此时可以结算水量。结算的高是此时的栈顶元素2位置的2，与arr[i]之间的最小值2与弹出元素1的差，所以积水的高= 1。结算的宽是i与栈顶元素索引值的差再减1，所以是4 - 2 - 1 = 1，这就是本次结算的储水量。这个结果计算的其实是下图中红色框内的水量。

继续上述流程，此时4位置的3依然不能入栈，所以将栈顶元素弹出。

弹出后栈不为空，可以结算水量。积水的高为arr[i] = 3和栈顶元素2的最小值，也就是2，减去弹出元素2，所以积水的高为0，无论宽度为多少，本次结算结果都为0。大家发现了吗？如果元素相等时选择入栈，那么其实是产生了一次无意义的计算，对计算结果并没有影响。

此时，4位置的3依然不能入栈，将栈顶元素1位置的2弹出。

栈不为空，所以可以结算水量。水量的高是min(3, 4) - 2 = 3 - 2 = 1，水量的宽是i - 栈顶元素index - 1 = 4 - 0 - 1 = 3，本次结算结果为1 * 3 = 3，也就是下图中黄色框内的区域。

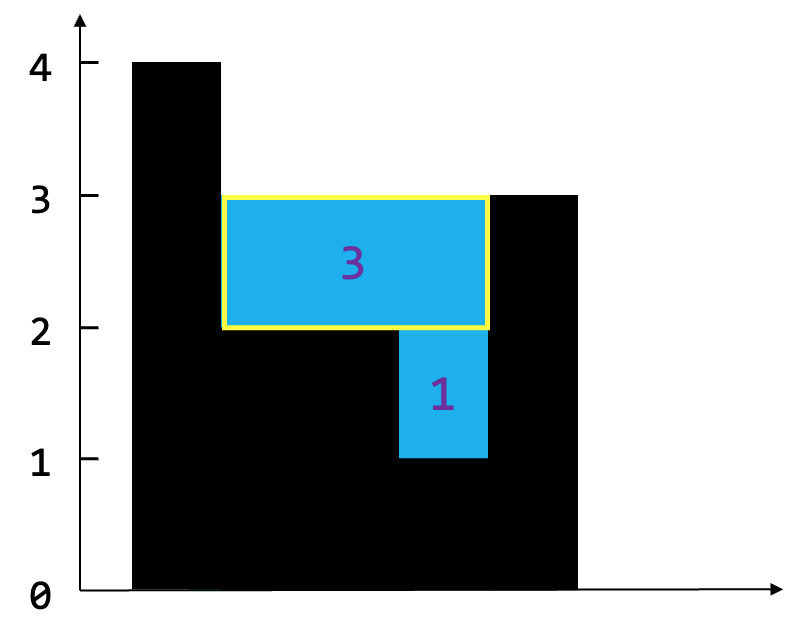
现在，4位置的3可以入栈了，数组遍历完成，流程结束。整体结果就是流程中每一轮结算的总和，即1 + 0 + 3 = 4。

我们再来看一下，如果元素相等时，我们将栈中元素弹出并结算会发生什么呢？

假设现在遍历到数组2位置的2，此时的状态应该是下面这样的。

此时我们将栈顶元素弹出，弹出后栈不为空，所以结算水量，结算的高等于遍历到的元素2位置的2和弹出后的栈顶元素0位置的4中的最小值，与弹出元素的差，所以显然结算水量的高等于0。

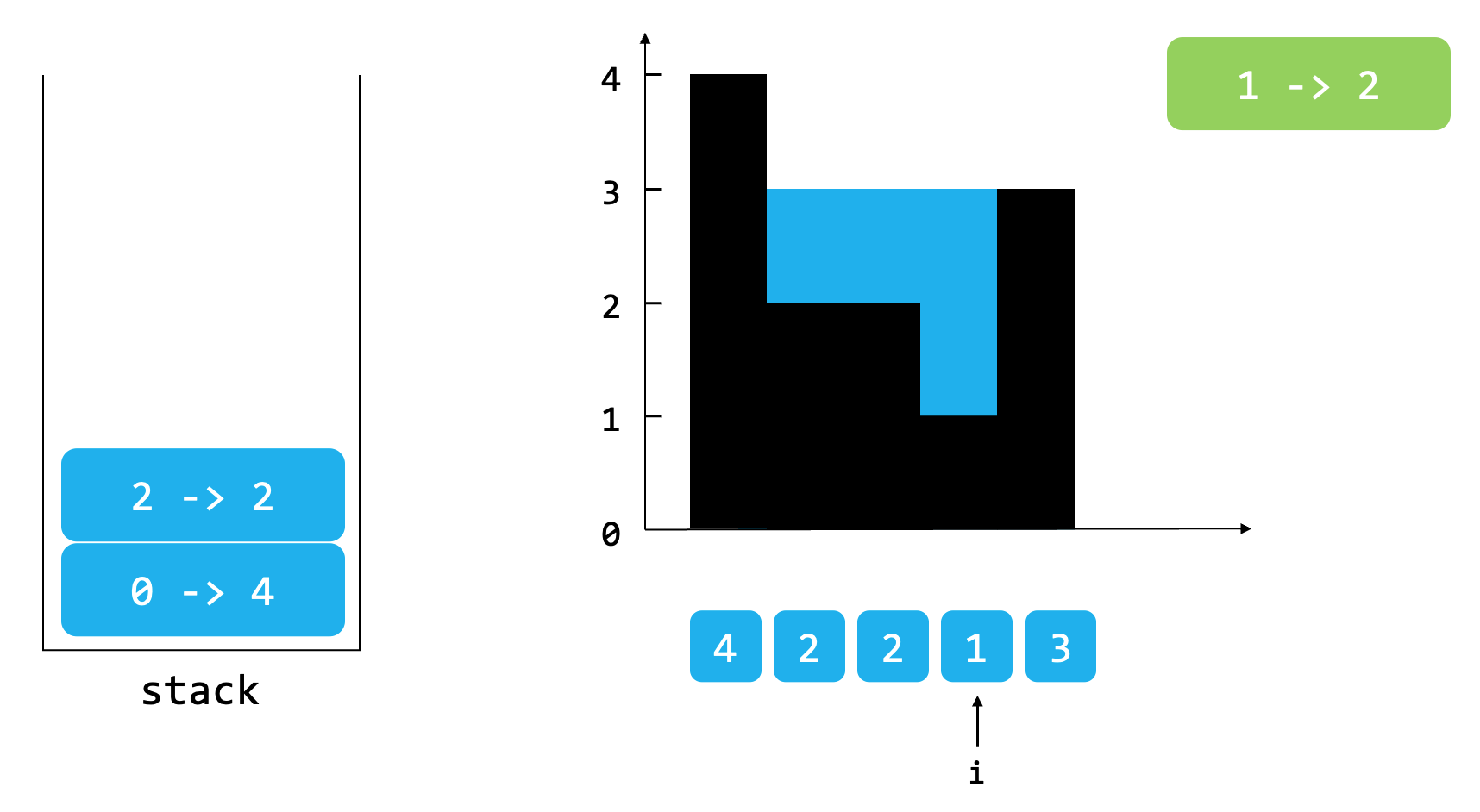
随后，数组3位置的1入栈，4位置的3不能入栈，所以弹出栈顶元素，这些都和上述流程一样。此时4位置的3依然不能入栈，所以将2位置的2弹出并结算水量。结算水量的高等于min(3, 4) - 2 = 1，结算水量的宽等于i - 栈顶元素的index - 1 = 4 - 0 - 1 = 3，本次结算结果为1 * 3 = 3，结果与上面流程也是完全一致的。

代码实现

java

public int trap(int[] height) {
    int res = 0;
    Stack<Integer> stack = new Stack<>();

    for (int i=0; i<height.length; i++) {
        while (!stack.isEmpty() && height[stack.peek()] < height[i]) {
            int pop = stack.pop();
            if (stack.isEmpty()) {
                break;
            }

            int width = i - stack.peek() - 1;
            int h = Math.min(height[i], height[stack.peek()]) - height[pop];
            res += width * h;
        }

        stack.push(i);
    }

    return res;
}

C++

int trap(vector<int>& height) {
    int res = 0;
    stack<int> stack;
    for (int i=0; i<height.size(); i++) {
        while (!stack.empty() && height[stack.top()] < height[i]) {
            int top = stack.top();
            stack.pop();
            if (stack.empty()) {
                break;
            }
            int width = i - stack.top() - 1;
            int h = min(height[i], height[stack.top()]) - height[top];
            res += width * h;
        }
        stack.push(i);
    }
    return res;
}

复杂度分析

• 时间复杂度：$O(n)$，每个元素最多入栈一次出栈一次
• 空间复杂度：$O(n)$，借助了一个大小为n的栈

如果觉得本篇文章对你有所帮助，请帮我点一个免费的赞和关注，这对我非常重要，谢谢！（手动鞠躬）

欢迎关注公众号：程序员冻豆腐，里面有我所有的原创文章