一 定义

概括地说： 随机变量Y是随机变量X的函数。

设g(x) 是一给定的连续函数， 称Y=g(X) 为随机变量X的一个函数， Y也是一个随机变量。当X取值

时，Y取值 .

~~~~~~~~~~~~~~

本文讨论连续型随机变量函数。

定理1:

设X为连续型随机变量， 其概率密度为， 设g(x) 是一严格单调的可导函数， 其值域为( α,  β ),  且 g'(x) ≠0,    记 x=h(y) 为 y=g(x)的反函数， 则 Y=g(X) 的概率密度

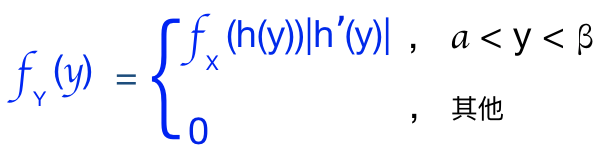
从定理可以看出，我们要确定g(x) 是为了求出反函数h(y),   进而求出导数h'(y),

h(y) 是以y为自变量的 表示x的函数。

 二  看例题

题1

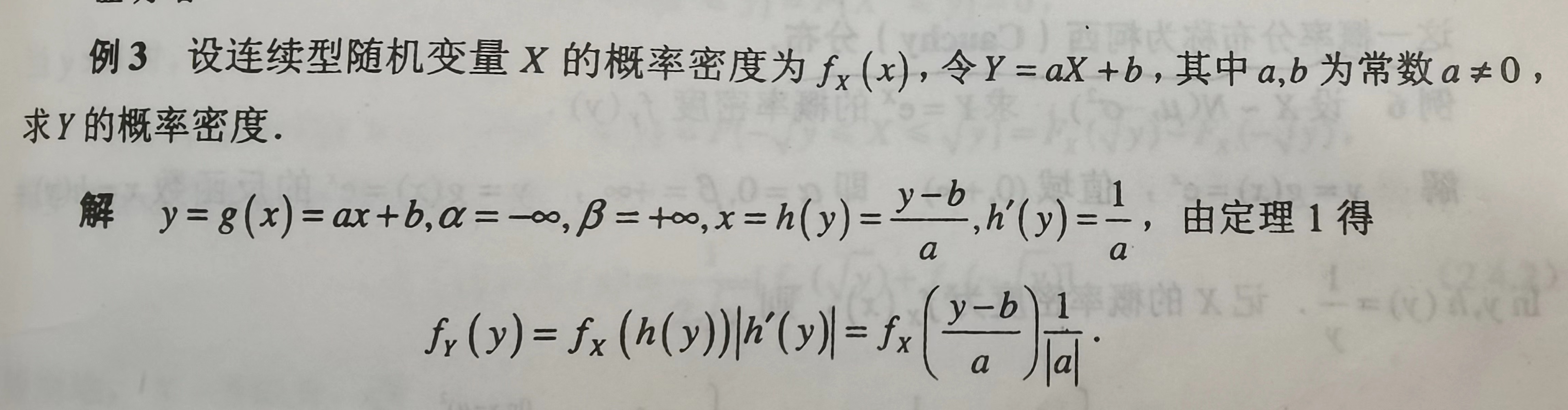
题2

设随机变量X在区间(0,  1) 服从均匀分布，  求Y = eˣ 的概率密度

解： 先用第一种方法：定理法求解

依题意， 易得出g(x) = eᕽ,  

所以得出h(y):   X = lnY,      h'(y) = 1/y.    

因为 X服从均匀分布，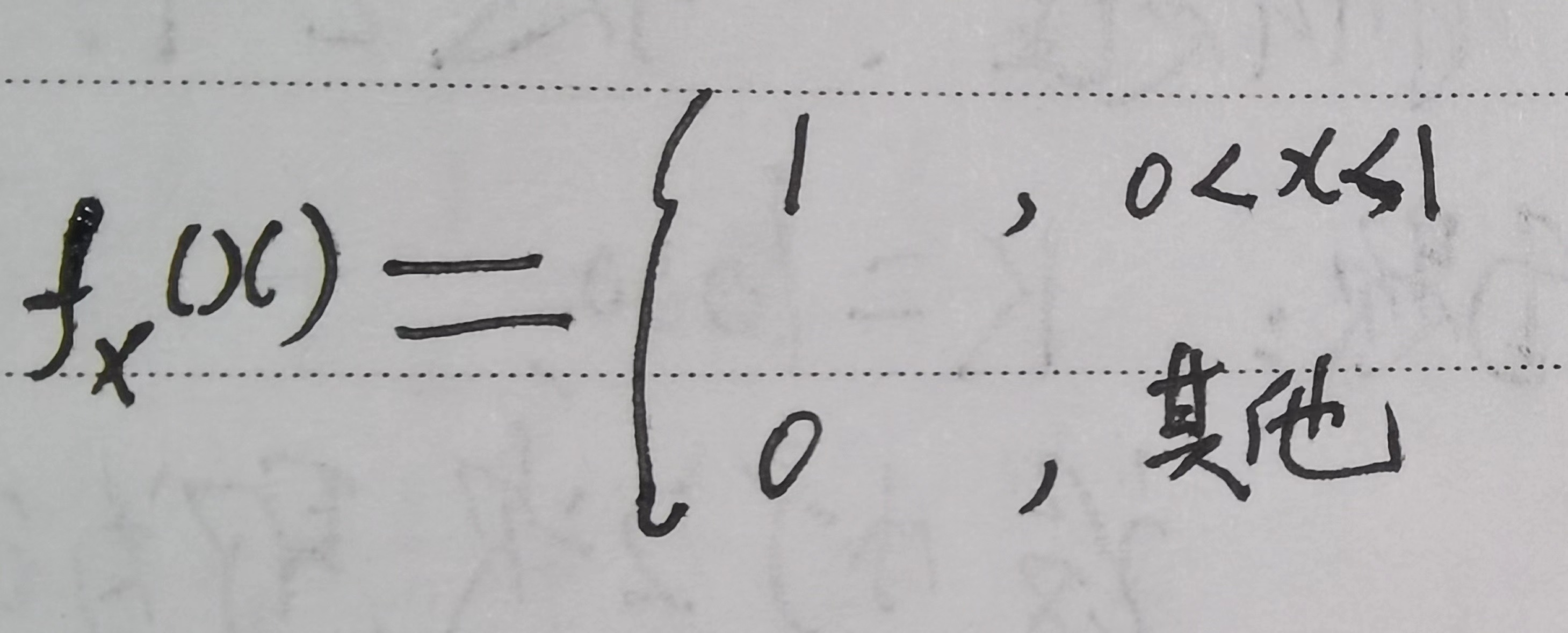  

现在需要求出 α,  β,   

α = min[g(-∞), g(+∞)] = g(0) =1,  β=max[g(-∞), g(+∞)]= g(1) = e,

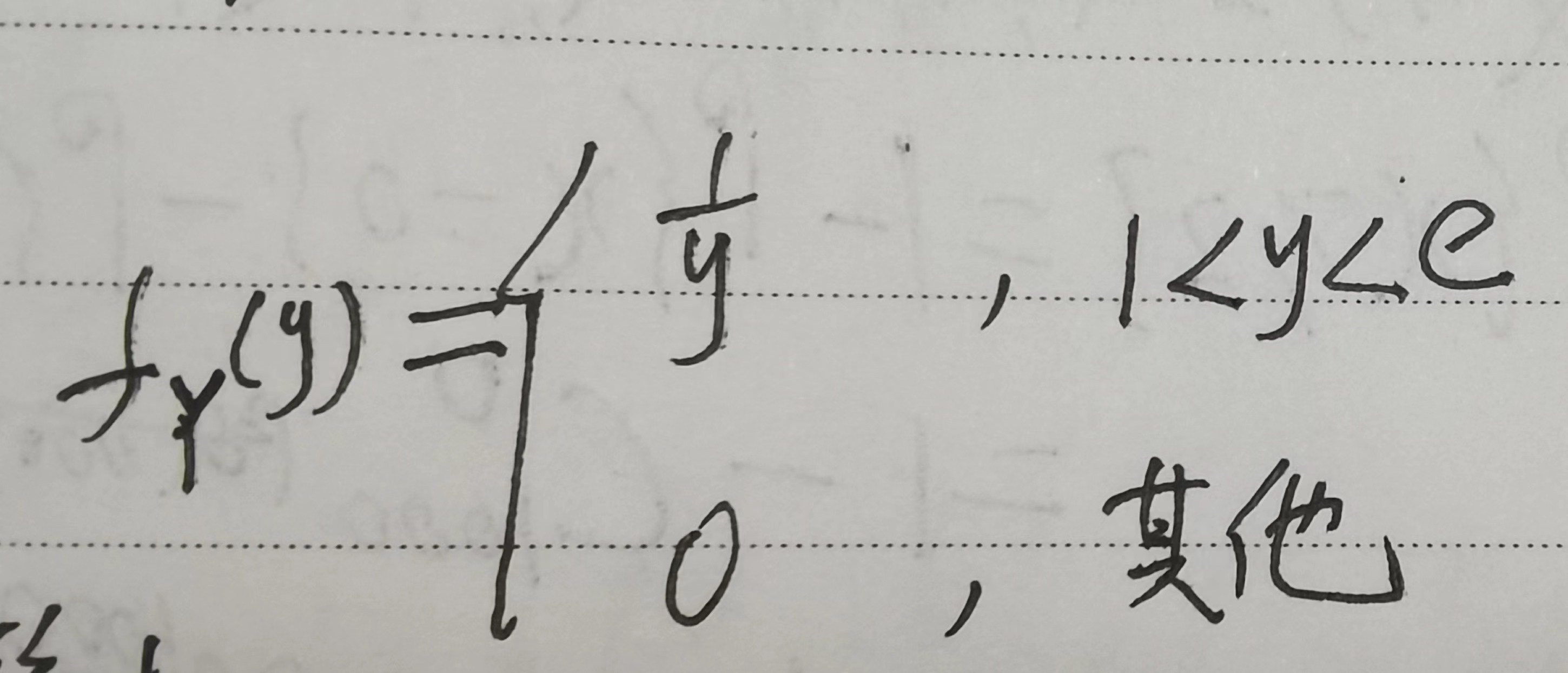
第二种方法 分布函数法，求解密度函数

基本过程是 先求出Fᵧ(y),  再对其求导数fᵧ(y).