文章目录
- 一、题目
- 二、解法
- 2.1 动态规划解法
- 2.2 数论解法
- 三、完整代码
所有的LeetCode题解索引,可以看这篇文章——【算法和数据结构】LeetCode题解。
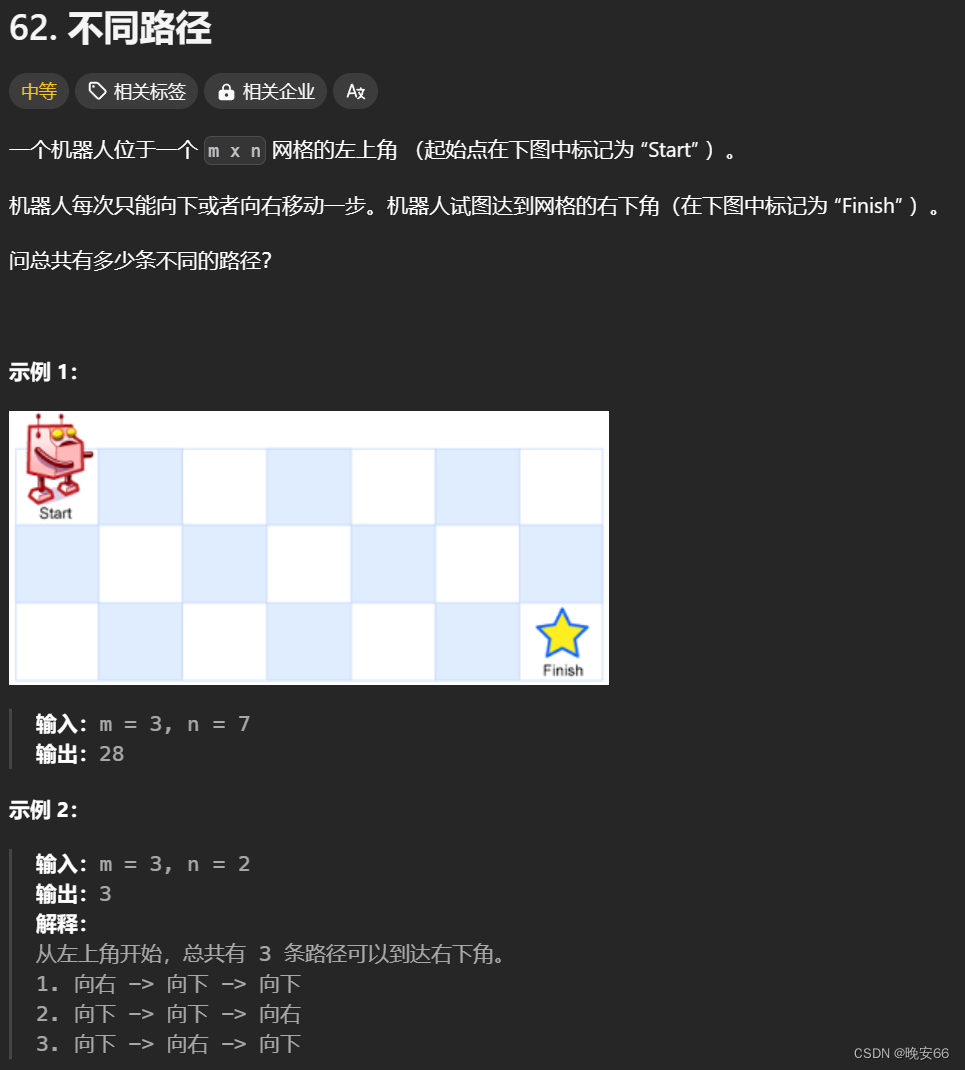
一、题目
二、解法
2.1 动态规划解法
思路分析:机器人只能向下或者向右移动,那么到达(i,j)位置的路径和(i-1,j)以及(i,j-1)有关。那么我们就得到的动态规划的表达式
d
p
[
i
]
[
j
]
=
d
p
[
i
−
1
]
[
j
]
+
d
p
[
i
]
[
j
−
1
]
dp[i][j]=dp[i-1][j]+dp[i][j-1]
dp[i][j]=dp[i−1][j]+dp[i][j−1]。其中,因为到达第一行和第一列位置的路径只有一条,因此dp数组中第一行第一列的元素都为1。根据如上信息,我们写出如下代码。
程序如下:
class Solution {
public:
int uniquePaths(int m, int n) {
vector<vector<int>> dp(m, vector<int>(n, 1));
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
return dp[m - 1][n - 1];
}
};
复杂度分析:
- 时间复杂度: O ( m ∗ n ) O(m*n) O(m∗n)。
- 空间复杂度: O ( m ∗ n ) O(m*n) O(m∗n)。
上述代码还可以再空间上进行压缩。从二维数组的角度来看,(i,j)位置的路径数等于它上方的元素和左边的元素之和。如果省略掉上方的元素,我们就能用一个一维数组来表示dp数组。迭代公式为 d p [ i ] = d p [ i ] + d o p [ i − 1 ] dp[i] = dp[i]+dop[i-1] dp[i]=dp[i]+dop[i−1],其中dop[i-1]代表左边元素,公式右边旧的dp[i]代表上方元素。最终输出为dp[n-1]。
class Solution {
public:
int uniquePaths(int m, int n) {
vector<int> dp(n);
for (int i = 0; i < n; i++) dp[i] = 1;
for (int j = 1; j < m; j++) {
for (int i = 1; i < n; i++) {
dp[i] += dp[i - 1];
}
}
return dp[n - 1];
}
};
复杂度分析:
- 时间复杂度: O ( m ∗ n ) O(m*n) O(m∗n)。
- 空间复杂度: O ( n ) O(n) O(n)。
2.2 数论解法
思路分析:从数学上我们可以知道,要到达终点,每次又只能走一步,那么总共需要的步数是
m
+
n
−
2
m+n-2
m+n−2,那么有
m
−
1
m-1
m−1步是要往下走的,那么问题就变成了在
m
+
n
−
2
m+n-2
m+n−2步中,
m
−
1
m-1
m−1步往下走有多少种组合。这是一个组合问题。因此,问题变成计算
C
m
+
n
−
2
m
−
1
=
(
m
+
n
−
2
)
!
(
m
−
1
)
!
(
n
−
1
)
!
=
(
m
+
n
−
2
)
∗
.
.
.
(
n
+
1
)
∗
n
(
m
−
1
)
!
C_{m+n-2}^{m-1}=\frac{(m+n-2)!}{{(m-1)!}{(n-1)!}}=\frac{(m+n-2)*...(n+1)*n}{(m-1)!}
Cm+n−2m−1=(m−1)!(n−1)!(m+n−2)!=(m−1)!(m+n−2)∗...(n+1)∗n。结合上述讨论,我们写出如下代码。代码当中,为了防止乘积中分子溢出,我们首先使用long long类型,并在循环中不断除以分母。
程序如下:
class Solution {
public:
int uniquePaths(int m, int n) {
long long numerator = 1; // 分子
int denominator = m - 1; // 分母
int num1 = m - 1, num2 = m + n - 2;
while (num1--) {
numerator *= (num2--);
while (denominator != 0 && numerator % denominator == 0) { // 分母不能为0, 且分子要能整除分母
numerator /= denominator;
denominator--;
}
}
return numerator;
}
};
复杂度分析:
- 时间复杂度: O ( m ) O(m) O(m)。
- 空间复杂度: O ( 1 ) O(1) O(1)。
三、完整代码
# include <iostream>
# include <vector>
using namespace std;
// 62、不同路径I
class Solution {
public:
int uniquePaths(int m, int n) {
vector<vector<int>> dp(m, vector<int>(n, 1));
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
return dp[m - 1][n - 1];
}
};
// 滚动数组削减空间复杂度
//class Solution {
//public:
// int uniquePaths(int m, int n) {
// vector<int> dp(n);
// for (int i = 0; i < n; i++) dp[i] = 1;
// for (int j = 1; j < m; j++) {
// for (int i = 1; i < n; i++) {
// dp[i] += dp[i - 1];
// }
// }
// return dp[n - 1];
// }
//};
// 数论方法
//class Solution {
//public:
// int uniquePaths(int m, int n) {
// long long numerator = 1; // 分子
// int denominator = m - 1; // 分母
// int num1 = m - 1, num2 = m + n - 2;
// while (num1--) {
// numerator *= (num2--);
// while (denominator != 0 && numerator % denominator == 0) { // 分母不能为0, 且分子要能整除分母
// numerator /= denominator;
// denominator--;
// }
// }
// return numerator;
// }
//};
int main() {
int m = 3, n = 2;
Solution s1;
int result = s1.uniquePaths(m, n);
cout << result << endl;
system("pause");
return 0;
}
end