既然要从0开始轨迹预测,那从哪开始写起呢?回想下自己的学习历程,真正有挑战性的不是模型结构,不是繁琐的训练和调参,而是数据的制作!!!
笔者自认为不是一个数学基础牢固的人,那么我们的轨迹预测之旅就从坐标转换开始吧~~~
由难至简,才能做到【删繁就简三秋树,领异标新二月花】,专注于轨迹预测的核心算法。
坐标和坐标系变换
- 1. 坐标系:
- 2. 坐标转换与坐标系转换
- 2.1 2D坐标转换
- 1. 平移(Translation)
- 2. 缩放(Scaling)
- 3. 旋转(Rotation)
- 2.2 2D坐标系转换
- 1. 坐标系平移
- 2. 坐标系旋转
- 3. 2D坐标系旋转平移总结
- 2.3 3D坐标系转换
- 1. 3D坐标系平移
- 2. 3D坐标系旋转
1. 坐标系:
二维直角坐标系,笛卡尔坐标系(Cartesian coordinate system),由两条相互垂直、相交于原点的数线构成的。

直角坐标系也可以推广至三维空间与高维空间 (higher dimension)。在原本的二维直角坐标系,再添加一个垂直于x-轴,y-轴的坐标轴,称为z-轴,叫做三维直角坐标系。
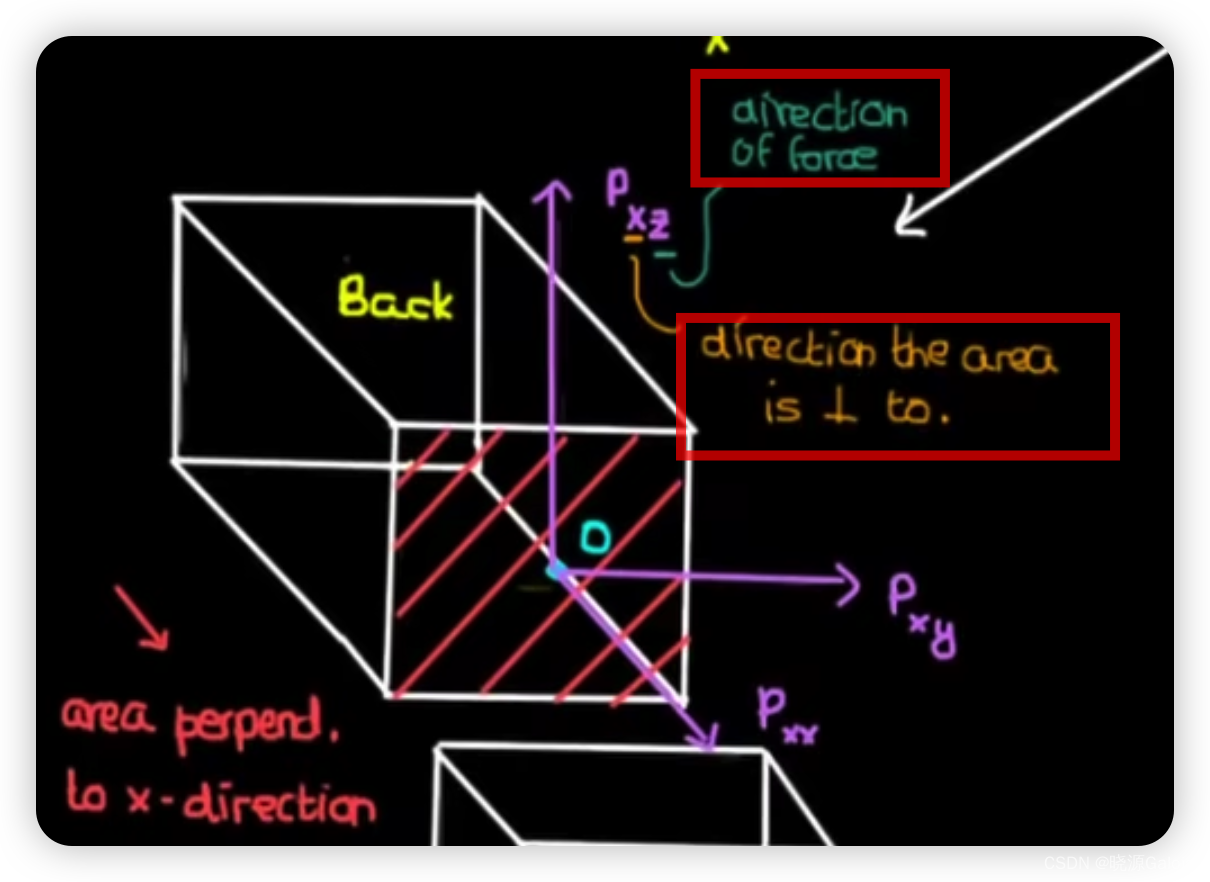
那么三维直角坐标系的x,y,z-轴的指向,以及绕x,y,z-轴旋转的方向该如何确定呢??
三维直角坐标系分两种,左手坐标系和右手坐标系,那么为什么要用左手和右手来区分呢?这是因为当确定了x-轴,y-轴方向之后,z-轴的方向有两种可能,它可以通过左手或右手来确定。
下面就是这两个坐标系 x,y,z-轴指向 的规则示意图(图中固定了x轴的正方向向右,y轴的正方向向上),其中大拇指、食指、中指分别对应于x-轴、y-轴、z-轴:
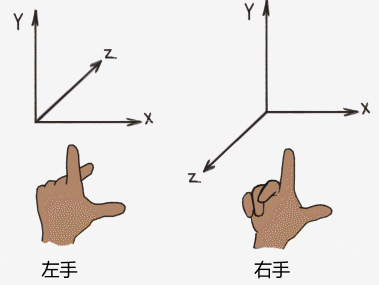
对坐标系使用左手与右手的命名,有一个作用就是用来方便 判断旋转的正方向,这就是左手螺旋法则和右手螺旋法则。例如对左手坐标系,确定一个旋转轴后,左手握住拳头,拇指指向旋转轴的正方向,四指弯曲的方向为旋转的正方向。相应地,右手坐标系就用右手来判定。确定了旋转的正方向后,在公式计算中就很容易知道是该使用正角度还是负角度了。下图就是右手的例子:

给定任意一个旋转角度的三维坐标系,如果按上面的方法判断旋转正方向,首先,你得确定这个坐标系是左手坐标系还是右手坐标系,这时你会先拿出一只手来,像上图一样摆好三根手指的姿势来比对给定坐标系的x、y、z轴正方向看是否一致。然后根据旋转轴的正方向,用相应的手来判断旋转正方向。
那么有什么快速判断的方法吗?

上图给出左右手坐标系绕z轴的旋转方向,从我们眼睛看屏幕的角度来看,它们绕z轴旋转的正方向都是逆时针。同理,绕y-轴和x-轴也可以获得相同的结论。则:对于任意旋转角度的三维坐标系(无需区分左右手),绕某一坐标轴旋转的正方向,与另外两个坐标轴的正方向顶端按X—>Y—>Z—>X的顺序进行指向的方向一致。
2. 坐标转换与坐标系转换
自由度的定义:自由度(Degree of Freedom,简称DOF)是指系统中可以自由变化的独立参数的数量,也就是系统的状态空间维度(有几个量可以调节)。
公式预警!!! 都是超级简单的向量的相加,相信我读完你会有收获哒!!!
2.1 2D坐标转换
1. 平移(Translation)
在2D空间中,我们经常需要将一个点平移到另一个位置(如下图所示)。假设空间中的一点P,其用坐标表示为(x,y);将其向 x方向平移 tx,向y方向平移ty, 假设平移后点的坐标为(x’,y’),则上述点的平移操作可以归纳为:
x
′
=
x
+
t
x
y
’
=
y
+
t
y
O
P
′
→
=
O
P
→
+
P
P
′
→
x' = x+t_x \\y’ = y+t_y \\ \overrightarrow{OP'} = \overrightarrow{OP} + \overrightarrow{PP'}
x′=x+txy’=y+tyOP′=OP+PP′

公式(1)又可以采用矩阵表述如下:
[ x ′ y ′ ] = [ 1 0 t x 0 1 t y ] [ x y ] \left[ \begin{array}{cc} x' \\ y'\end{array} \right] = \left[ \begin{array}{cc} 1 & 0&t_x\\ 0&1&t_y\end{array} \right]\left[ \begin{array}{cc} x \\ y\end{array} \right] [x′y′]=[1001txty][xy]
2. 缩放(Scaling)
其中,s_x和s_y分别是沿x和y轴的缩放因子。
x
′
=
s
x
x
y
’
=
s
y
s
O
P
′
→
=
s
O
P
→
x' = s_xx \\y’ = s_ys \\ \overrightarrow{OP'} = s\overrightarrow{OP}
x′=sxxy’=sysOP′=sOP

齐次坐标的形式:
[
x
′
y
′
1
]
=
[
s
x
0
1
0
s
y
1
0
0
1
]
[
x
y
1
]
\left[ \begin{array}{cc} x' \\ y'\\ 1\end{array} \right] = \left[ \begin{array}{cc} s_x & 0&1\\ 0&s_y&1 \\ 0&0&1\end{array} \right]\left[ \begin{array}{cc} x \\ y \\1\end{array} \right]
x′y′1
=
sx000sy0111
xy1
3. 旋转(Rotation)
点P(x,y)绕坐标系原点旋转 θ \theta θ角得到点P’(x‘,y’)有:

将OP与x-轴正方向的夹角记做
β
\beta
β,OP的长度为r,且
r
c
o
s
β
=
x
rcos\beta = x
rcosβ=x,
r
s
i
n
β
=
y
rsin\beta=y
rsinβ=y,则P‘的坐标可推导为:
x
′
=
r
c
o
s
(
θ
+
β
)
=
r
(
c
o
s
θ
c
o
s
β
−
s
i
n
θ
s
i
n
β
)
=
r
c
o
s
β
c
o
s
θ
−
r
s
i
n
β
s
i
n
θ
y
′
=
r
s
i
n
(
θ
+
β
)
=
r
(
s
i
n
θ
c
o
s
β
+
c
o
s
θ
s
i
n
β
)
=
r
c
o
s
β
s
i
n
θ
+
r
s
i
n
β
c
o
s
θ
x' = rcos(\theta + \beta) = r(cos\theta cos\beta - sin\theta sin\beta) = rcos\beta cos\theta -rsin\beta sin\theta \\ y' = rsin(\theta + \beta) = r(sin\theta cos\beta + cos\theta sin\beta) = rcos\beta sin\theta +rsin\beta cos\theta \\
x′=rcos(θ+β)=r(cosθcosβ−sinθsinβ)=rcosβcosθ−rsinβsinθy′=rsin(θ+β)=r(sinθcosβ+cosθsinβ)=rcosβsinθ+rsinβcosθ
x ′ = x c o s θ − y s i n θ y ′ = x s i n θ + y c o s θ x' = xcos\theta - ysin\theta \\ y'=xsin\theta+ycos\theta x′=xcosθ−ysinθy′=xsinθ+ycosθ
同理写成齐次坐标的形式:
[
x
′
y
′
1
]
=
[
c
o
s
θ
−
s
i
n
θ
1
s
i
n
θ
c
o
s
θ
1
0
0
1
]
[
x
y
1
]
\left[ \begin{array}{cc} x' \\ y'\\ 1\end{array} \right] = \left[ \begin{array}{cc} cos\theta & -sin\theta&1\\ sin\theta&cos\theta&1 \\ 0&0&1\end{array} \right]\left[ \begin{array}{cc} x \\ y \\1\end{array} \right]
x′y′1
=
cosθsinθ0−sinθcosθ0111
xy1
2.2 2D坐标系转换
理解了2D坐标转换,2D坐标系的转换(坐标点不动,坐标系动-横看成岭侧成峰)可以看成2D坐标转换的逆转换:
坐标系向左平移 = 坐标点在原坐标系基础上向右平移;
坐标系绕轴顺时针旋转 = 坐标点在原坐标系的基础上绕轴逆时针旋转;
1. 坐标系平移
红色坐标系相对于黑色坐标系中平移的距离为(i, j)
红色点在红色坐标系的位置为(x, y),则红色点在黑色坐标系的表示如下图所示:
图中示例,坐标系向左向下平移,相当于P点像右像上平移。

x
′
=
i
+
x
y
′
=
j
+
y
O
P
′
→
=
O
O
′
→
+
O
′
P
→
=
(
i
,
j
)
+
(
x
,
y
)
=
(
i
+
x
,
j
+
y
)
x'=i+x \\ y'=j+y \\ \overrightarrow{OP'} = \overrightarrow{OO'}+\overrightarrow{O'P} = (i, j) + (x, y) = (i+x,j+y)
x′=i+xy′=j+yOP′=OO′+O′P=(i,j)+(x,y)=(i+x,j+y)
将坐标系的平移写成齐次坐标的形式:
[
x
′
y
′
1
]
=
[
1
0
i
0
1
j
0
0
1
]
[
x
y
1
]
\left[ \begin{array}{cc} x' \\ y'\\ 1\end{array} \right] = \left[ \begin{array}{cc} 1 & 0&i\\ 0&1&j \\ 0&0&1\end{array} \right]\left[ \begin{array}{cc} x \\ y \\1\end{array} \right]
x′y′1
=
100010ij1
xy1
2. 坐标系旋转

已知 红点P在蓝色坐标系的位置(x, y),也知道蓝色坐标系相较于黑色坐标系顺时针旋转的角度θ。
求解: 红点在黑色坐标系同的位置(X‘, Y’)?
蓝色坐标系相较于黑色坐标系顺时针旋转的角度θ,相当于计算P点在蓝色系内绕远点逆时针旋转θ
向量分解的方法推导:
将P点的坐标,沿黑色坐标系分解:

x
′
=
x
c
o
s
θ
−
y
s
i
n
θ
y
′
=
x
s
i
n
θ
+
y
c
o
s
θ
x'=xcos\theta-ysin\theta \\ y'=xsin\theta+ycos\theta
x′=xcosθ−ysinθy′=xsinθ+ycosθ
写成齐次坐标的形式:
[
x
′
y
′
1
]
=
[
c
o
s
θ
−
s
i
n
θ
1
s
i
n
θ
c
o
s
θ
1
0
0
1
]
[
x
y
1
]
\left[ \begin{array}{cc} x' \\ y'\\ 1\end{array} \right] = \left[ \begin{array}{cc} cos\theta & -sin\theta&1\\ sin\theta&cos\theta&1 \\ 0&0&1\end{array} \right]\left[ \begin{array}{cc} x \\ y \\1\end{array} \right]
x′y′1
=
cosθsinθ0−sinθcosθ0111
xy1
3. 2D坐标系旋转平移总结
已知 红点在蓝色坐标系的位置P(xb, yb),也知道蓝色坐标系相较于黑色坐标系 旋转的角度θ, 其中 蓝色坐标系的原点在黑色坐标系中的位置为(δx, δy).
求解: 红点在黑色坐标系同的位置(xa, ya)?

以向量的方式推导:
P点在A系下的坐标可以用向量
O
a
P
→
\overrightarrow{O_aP}
OaP表示:
O
a
P
→
=
O
a
O
b
→
+
O
b
P
→
\overrightarrow{O_aP} = \overrightarrow{O_aO_b}+\overrightarrow{O_bP}
OaP=OaOb+ObP
其中
O
a
O
b
→
=
(
δ
x
,
δ
y
)
\overrightarrow{O_aO_b}=(\delta_x,\delta_y)
OaOb=(δx,δy),那么我们该如何表示向量
O
b
P
→
\overrightarrow{O_bP}
ObP的坐标值呢?
在此处有个误区,大家可能会觉得 O b P → = ( x b , y b ) \overrightarrow{O_bP}=(x_b,y_b) ObP=(xb,yb)。其实不是这样的,(xb,yb)坐标表示的是点P在B坐标系中的位置,视角是站在B坐标系上的,此时我们的视角应该是在A坐标系,或者是和A坐标系平行的。
所以,我们应该将B坐标系进行旋转,保证和A坐标系平行的,如下图所示。

根据前面旋转部分的推导,我们可以得到:
O
b
P
→
=
[
c
o
s
θ
−
s
i
n
θ
s
i
n
θ
c
o
s
θ
]
[
x
b
y
b
]
\overrightarrow{O_bP}=\left[ \begin{array}{cc} cos\theta & -sin\theta\\ sin\theta&cos\theta \end{array} \right]\left[ \begin{array}{cc} x_b \\ y_b \end{array} \right]
ObP=[cosθsinθ−sinθcosθ][xbyb]
则根据公式(14),
O
a
P
→
=
[
x
a
y
a
]
=
[
δ
x
δ
y
]
+
[
c
o
s
θ
−
s
i
n
θ
s
i
n
θ
c
o
s
θ
]
[
x
b
y
b
]
=
[
c
o
s
θ
∗
x
b
+
δ
x
−
s
i
n
θ
∗
y
b
s
i
n
θ
∗
x
b
+
δ
y
+
c
o
s
θ
∗
y
b
]
\overrightarrow{O_aP} = \left[\begin{array}{} x_a \\ y_a \end{array}\right] =\left[\begin{array}{} \delta_x \\ \delta_y \end{array}\right] + \left[\begin{array}{} cos\theta & -sin\theta \\ sin\theta & cos\theta \end{array}\right]\left[\begin{array}{} x_b \\ y_b \end{array}\right] = \left[\begin{array}{} cos\theta*x_b+\delta_x -sin\theta*y_b \\ sin\theta*x_b+\delta_y + cos\theta*y_b \end{array}\right]
OaP=[xaya]=[δxδy]+[cosθsinθ−sinθcosθ][xbyb]=[cosθ∗xb+δx−sinθ∗ybsinθ∗xb+δy+cosθ∗yb]
写成齐次坐标的形式:
[
x
a
y
a
1
]
=
[
c
o
s
θ
−
s
i
n
θ
δ
x
s
i
n
θ
c
o
s
θ
δ
y
0
0
1
]
[
x
b
y
b
1
]
\left[ \begin{array}{cc} x_a \\ y_a\\ 1\end{array} \right] = \left[ \begin{array}{cc} cos\theta & -sin\theta&\delta_x\\ sin\theta&cos\theta&\delta_y \\ 0&0&1\end{array} \right]\left[ \begin{array}{cc} x_b \\ y_b \\1\end{array} \right]
xaya1
=
cosθsinθ0−sinθcosθ0δxδy1
xbyb1
T T T表示transform,变换的意思。
B A T ^A_BT BAT表示的是 由B坐标系变换为A坐标系的意思。
对于2D坐标系的旋转和平移大致上我们可以得到以下:
P a = B A T ⋅ P b P b = B A T − 1 ⋅ P a P_a =_B^AT ·P_b \\ P_b =_B^AT^{-1} ·P_a Pa=BAT⋅PbPb=BAT−1⋅Pa
2.3 3D坐标系转换
3D坐标系转换,仅仅是添加了一维z-轴,所使用的基础公式和2D并无差异。
1. 3D坐标系平移
同样已知 红色点在蓝色坐标系的位置为(x1,y1,z1)
蓝色坐标系的原点在黑色坐标系中的位置为(δx,δy,δz)
求解: 红色点在黑色坐标系中的位置点(x2,y2,z2)?

根据向量的加法有:
O
2
P
→
=
O
2
O
1
→
+
O
1
P
→
=
(
δ
x
,
δ
y
,
δ
z
)
+
(
x
1
,
y
1
,
z
1
)
\overrightarrow{O_2P} = \overrightarrow{O_2O_1} + \overrightarrow{O_1P} = (\delta_x,\delta_y,\delta_z)+(x_1,y_1,z_1)
O2P=O2O1+O1P=(δx,δy,δz)+(x1,y1,z1)
同样,用齐次坐标表示:
[
x
2
y
2
z
2
]
=
[
1
0
0
δ
x
0
1
0
δ
y
0
0
1
δ
z
]
[
x
1
y
1
z
1
]
\left[\begin{array}{cc} x_2 \\ y_2 \\z_2 \end{array} \right] = \left[ \begin{array}{cc} 1 & 0&0&\delta_x\\ 0&1&0&\delta_y \\0&0&1&\delta_z\end{array} \right]\left[ \begin{array}{cc} x_1 \\ y_1 \\z_1\end{array} \right]
x2y2z2
=
100010001δxδyδz
x1y1z1
2. 3D坐标系旋转
-
绕z轴旋转(同2D旋转):
绕z-轴旋转,z坐标保持不变
[ x 2 y 2 z 2 ] = [ c o s θ − s i n θ 0 s i n θ c o s θ 0 0 0 1 ] [ x 1 y 1 z 1 ] \left[ \begin{array}{cc} x_2 \\ y_2\\ z_2\end{array} \right] = \left[ \begin{array}{cc} cos\theta & -sin\theta&0\\ sin\theta&cos\theta&0 \\ 0&0&1\end{array} \right]\left[ \begin{array}{cc} x_1 \\ y_1 \\z_1\end{array} \right] x2y2z2 = cosθsinθ0−sinθcosθ0001 x1y1z1 -
绕y轴旋转:
绕y-轴旋转,z坐标保持不变
[ x 2 y 2 z 2 ] = [ c o s θ 0 s i n θ 0 1 0 − s i n θ 0 c o s θ ] [ x 1 y 1 z 1 ] \left[ \begin{array}{cc} x_2 \\ y_2\\ z_2\end{array} \right] = \left[ \begin{array}{cc} cos\theta &0& sin\theta\\0&1&0\\ -sin\theta&0&cos\theta \\ \end{array} \right]\left[ \begin{array}{cc} x_1 \\ y_1 \\z_1\end{array} \right] x2y2z2 = cosθ0−sinθ010sinθ0cosθ x1y1z1
你是不是也发现了,这个公式好像和2D旋转的不大一样?别急,手动画一下旋转图像你就会明白的~
还记得前面介绍,旋转角的正负吗?忘记的同学可以看一下本篇文章的第一部分坐标系, 旋转的正方向为X->Y->Z->X,而此时绕y轴旋转的角度theta,为旋转的负方向,所以此时应在原旋转矩阵的基础上取逆矩阵即可~,这也是为什么绕Y轴旋转的公式不一样的原因!!!
-
绕X轴旋转:
x坐标保持不变
[ x 2 y 2 z 2 ] = [ 1 0 0 0 c o s θ s i n θ 0 − s i n θ c o s θ ] [ x 1 y 1 z 1 ] \left[ \begin{array}{cc} x_2 \\ y_2\\ z_2\end{array} \right] = \left[ \begin{array}{cc} 1&0&0\\0&cos\theta & sin\theta\\ 0&-sin\theta&cos\theta \\ \end{array} \right]\left[ \begin{array}{cc} x_1 \\ y_1 \\z_1\end{array} \right] x2y2z2 = 1000cosθ−sinθ0sinθcosθ x1y1z1 -
3D坐标系的旋转:
R z y x = R x ( α ) R y ( β ) R z ( γ ) R_{zyx}=R_x(\alpha)R_y(\beta)R_z(\gamma) Rzyx=Rx(α)Ry(β)Rz(γ)
将上述三个矩阵依次相乘:

上述矩阵看成:
[
R
11
R
12
R
13
R
21
R
22
R
23
R
31
R
32
R
33
]
\left[ \begin{array}{cc} R_{11}&R_{12}&R_{13} \\ R_{21}&R_{22}&R_{23}\\ R_{31}&R_{32}&R_{33}\end{array} \right]
R11R21R31R12R22R32R13R23R33
如果我想通过旋转矩阵反求旋转角度,该如何做呢?观察旋转矩阵各个项之间的关系。
三角函数中,如果要求解一个角度值,可以通过:
θ
=
a
r
c
t
a
n
(
s
i
n
θ
,
c
o
s
θ
)
\theta=arctan(sin\theta,cos\theta)
θ=arctan(sinθ,cosθ)
求绕x-轴旋转的角度:
α
=
a
r
c
t
a
n
(
R
21
,
R
11
)
\alpha=arctan(R_{21},R_{11})
α=arctan(R21,R11)
求绕y-轴旋转的角度:
求解绕y轴旋转有点麻烦,已知公式(24),则:
β
=
a
r
c
t
a
n
(
−
R
31
,
c
o
s
β
)
\beta=arctan(-R_{31},cos\beta)
β=arctan(−R31,cosβ)
那么
c
o
s
β
cos\beta
cosβ怎么求呢?我们继续观察
R
11
R_{11}
R11和
R
21
R_{21}
R21, 他们分别是
c
o
s
(
α
)
⋅
c
o
s
(
β
)
cos(α)⋅cos(β)
cos(α)⋅cos(β) 和
s
i
n
(
α
)
⋅
c
o
s
(
β
)
sin(α)⋅cos(β)
sin(α)⋅cos(β)
尝试使用
R
11
2
+
R
21
2
\sqrt{R_{11}^2+R_{21}^2}
R112+R212,化简后得到:
c
o
s
β
=
R
11
2
+
R
21
2
cos\beta =\sqrt{R_{11}^2+R_{21}^2}
cosβ=R112+R212
则:
β
=
a
r
c
t
a
n
(
−
R
31
,
R
11
2
+
R
21
2
)
\beta=arctan(-R_{31},\sqrt{R_{11}^2+R_{21}^2})
β=arctan(−R31,R112+R212)
求绕z-轴的旋转角度:
γ
=
a
r
c
t
a
n
(
R
32
,
R
33
)
\gamma=arctan(R_{32},R_{33})
γ=arctan(R32,R33)