适用平台:Matlab2023版本及以上
本原创程序提出的ZOA-PCNN-AT-SVM故障识别模型还没有人写!在此基础上进一步对参考模型进行多重改进,程序注释清晰,干货满满,下面对文章和程序做简要介绍!
①识别模型部分参考中文EI期刊《电力自动化设备》12月29号网络首发文献:《基于格拉姆角场与并行CNN的并网逆变器开关管健康诊断》;②优化模型部分参考知名SCI、EI期刊《IEEE Access》2022年10月发表的论文《Zebra Optimization Algorithm》
该算法提出时间很短,目前还没有套用这个算法的文献
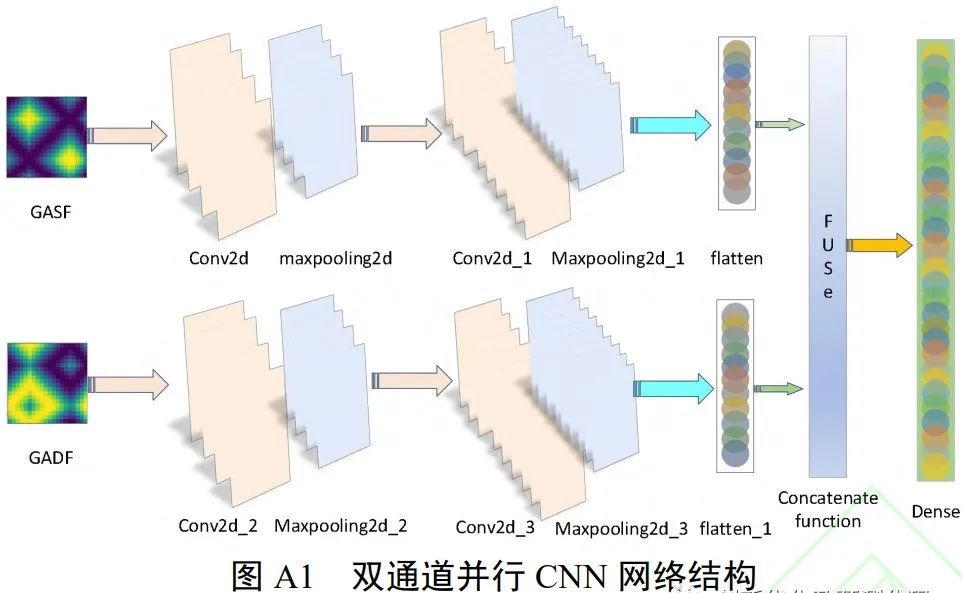
识别模型原文献解读:这篇文献中,首先,采集一维故障电压与电流信号的时序序列;其次,利用格拉姆角场对其进行变换,将两种一维时序信号转化为格拉姆角场,最后,将生成的两组图像同时送入CNN进行并行学习训练,实现逆变器故障诊断。

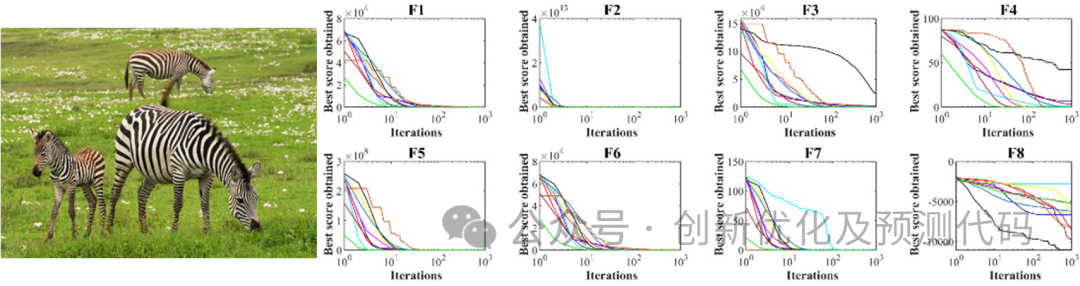
斑马优化ZOA简介:ZOA斑马优化的基本灵感来自斑马在自然界中的行为。ZOA模拟了斑马的觅食行为及其对捕食者攻击的防御策略,对 ZOA 步骤进行描述,然后进行数学建模。ZOA 在优化方面的性能根据 68 个基准函数进行评估,包括单峰、高维多模态、固定维多模态。将ZOA获得的结果与九种知名算法GWO、TLBO、GA、MPA、PSO、QANA、TSA、WOA和GSA的性能进行了比较,仿真结果表明,ZOA能够通过在探索和开发之间建立适当的平衡来解决优化问题,并且与9种竞争算法相比具有更优越的性能。并在四个实际工程问题上对ZOA进行了测试。
模型改进:我们提出的模型在上述文献模型基础上作出多重改进,提出的ZOA-PCNN-AT-SVM故障识别模型:采用双支路结构,仅需原始故障波形数据,即可根据波形数据,将一维序列转化为二维格拉姆求和场图像。将图像同时输入PCNN-AT-SVM模型,用ZOA对模型中的超参数进行寻优,提供两条支路提取的特征图,提供原始样本和特征样本之间的分布情况,提高模型可解释性,并计算精确度、召回率、精确率、F1分数等评价指标。故障识别流程如下:https://mbd.pub/o/bread/ZZmZmp5q

七重创新点:
1、时序图像化:将一维时序信号转化为二维图像,从而更全面地描述数据的特征。这有助于提取更丰富、更有区别性的特征,从而提高分类和识别的准确性。
2、空间特征学习:CNN(卷积神经网络)在图像处理中表现出色,能够有效地学习图像的空间特征和局部模式。将CNN用于图像数据的处理可以帮助提取图像的纹理、形状和边缘等特征,有助于更准确地进行分类和故障识别。
3、双支路结构:利用两个分支CNN学习不同的图像权重值,双支路高维特征互补,使得深层空间特征得到显著增强。
4、多头自注意力机制:融合多头注意力机制有效把握提取特征的贡献程度,将特征进行重点强化,提高故障识别的准确率。
5、可解释性:为提升模型的可解释性,应用t-SNE可解释性算法对各个支路模块的特征图进行可视化;对比原始样本和ZOA-PCNN-AT-SVM提取特征后的样本分布情况。
6、改进输出结构:将原始的Softmax层改进为SVM,Softmax作为概率方法,会受到异常值的影响,而SVM采用样本分布的边缘来分类一定距离内的故障样本,对异常值具有更强的鲁棒性。
7、超参数优化:斑马优化算法ZOA对模型中的难以确定的学习率、支路1卷积核大小、支路2卷积核大小等参数进行寻优,使得模型的结构更加合理,提高了故障识别精度。
适用领域:适用于各种数据分类场景,如滚动轴承故障、变压器油气故障、电力系统输电线路故障区域、绝缘子、配网、电能质量扰动,等领域的识别、诊断和分类。
以下手把手带大家分析程序的结果:
数据格式:一行一个样本,最后一列为样本所属的故障类型标签直接替换数据就可以,使用Excel表格直接导入,不需要对程序大幅修改。程序内有详细注释,便于理解程序运行。

程序结果:(由上述一维序列自动转化为格拉姆图像)

模型结构:

PCNN 双支路实现特征可视化(证明2条支路的特征不同,有互补性)

与原始样本相比,ZOA-PCNN-SVM 能够实现相同样本聚合,实现同类别故障样本的聚合(不同类间的区分,同类间的聚合)

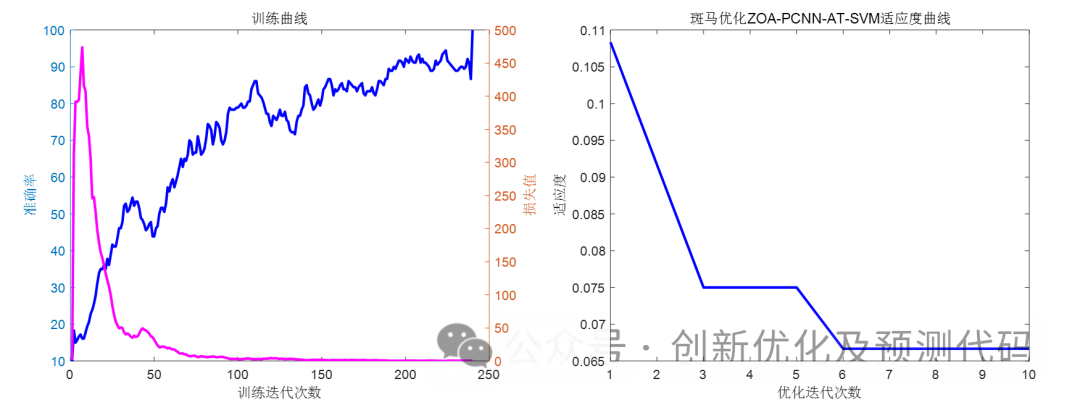
模型训练曲线:

训练曲线:和 斑马优化ZOA适应度曲线:
部分图片来源于网络,侵权联系删除!
部分代码:
%% %%%%%%%%%%%%%%%%%%% ZOA-PCNN-SVM算法 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%来自公众号:《创新优化及预测代码》%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
完整代码:https://mbd.pub/o/bread/ZZmZmp5q
%% 定义ZOA参数
Fun_name='objectiveFunction1'; %% 目标函数
SearchAgents = 2; %% 斑马数量(种群规模)
Max_iterations = 10; %% 最大迭代次数
%% 目标函数
fitness = @objectiveFunction; %% 获取目标函数信息
lowerbound = [0.001, 1, 2]; %% 寻优参数下限 [学习率, 支路1卷积核大小, 支路2卷积核大小];
upperbound = [0.01, 5, 6]; %% 寻优参数上限 [学习率, 支路1卷积核大小, 支路2卷积核大小];
dimension = 3; %% 有几个需要优化的参数就是几维
%% ZOA-PCNN-SVM优化参数优化(学习率、支路1卷积核、支路2卷积核)
[Best_score,Best_pos,ZOA_curve,bestPred,Best_PCNN_AT_SVM, Best_info]=zoa( ...
SearchAgents,Max_iterations,lowerbound,upperbound,dimension,fitness); % 使用斑马优化算法计算目标函数
%% 保存优化数据
% 使用save函数保存变量
save(fullfile(save_path, 'bestPred.mat'), 'bestPred'); %% 最佳预测结果
save(fullfile(save_path, 'Best_PCNN_SVM.mat'), 'Best_PCNN_AT_SVM'); %% 最佳网络
save(fullfile(save_path, 'Best_info.mat'), 'Best_info'); %% 最佳网络下的迭代曲线
save(fullfile(save_path, 'ZOA_curve.mat'), 'ZOA_curve'); %% 适应度曲线
%% 优化结果可视化
disp(['斑马优化后的神经网络识别误差:', num2str((1-Best_score).*100), '%']);
figure
plot(ZOA_curve,LineWidth=2,Color=[0 0 1]);
title('斑马优化ZOA-PCNN-AT-SVM适应度曲线')
xlabel('优化迭代次数');
ylabel('适应度');
% ZOA优化后-PCNN网络的结构参数信息
analyzeNetwork(Best_PCNN_AT_SVM) ;
%% 查看网络结构
figure
plot(Best_PCNN_AT_SVM)
title("斑马优化后的ZOA-PCNN-AT-SVM模型") % SVM属于机器学习部分,故无法绘制,实际上是ZOA-PCNN-AT-SVM模型 SVM取代原模型中的softmax层
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%来自公众号:《创新优化及预测代码》%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%% 过程步骤一: PCNN 双支路实现特征可视化(证明2条支路的特征不同,有互补性)
%% %%%%%%%%%%%%%%%%%%% 分别绘制双支路的特征图 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%来自公众号:《创新优化及预测代码》%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%% 激活支路1末端的maxpool1层
layer1 = 'maxpool1';
LayersNeed = activations(Best_PCNN_AT_SVM,imdsTest,layer1,'OutputAs','channels');% 支路1
%% 支路1所提取特征
% 前4个池化核
figure;
for i = 1:4 % 前4个特征图 i的不能超过池化核的个数
LayersFeature = LayersNeed(:,:,i,2);% 随机针对第2个样本的特征提取过程
subplot(2, 2, i); % 创建池化层1的第i个子图
image(LayersFeature, 'CDataMapping', 'scaled');
colormap(hsv);
xlim([1, size(LayersFeature, 2)]); % 限制坐标轴
ylim([1, size(LayersFeature, 1)]); % 限制坐标轴
axis off; % 关闭坐标轴显示
box on;
title(['特征图', num2str(i)]); % 添加特征图标题
end部分图片来源于网络,侵权联系删除!