ICPP 2019 Paper 分布式元数据论文汇总
问题
为了同时解决元数据局部性和元数据服务器的负载均衡。
现有方法缺陷
-
基于哈希的方法:zFS [16],CalvinFS [21],DROP [24],AngleCut [8]
-
静态子树划分:HDFS [6], NFS [14], PVFS2 [25], CXFS [10] and Coda [17]
-
动态子树划分:Ceph [22], Kosha [2] and GIGA+ [13]
-
其他:Dynamic Dir-Grain [23]
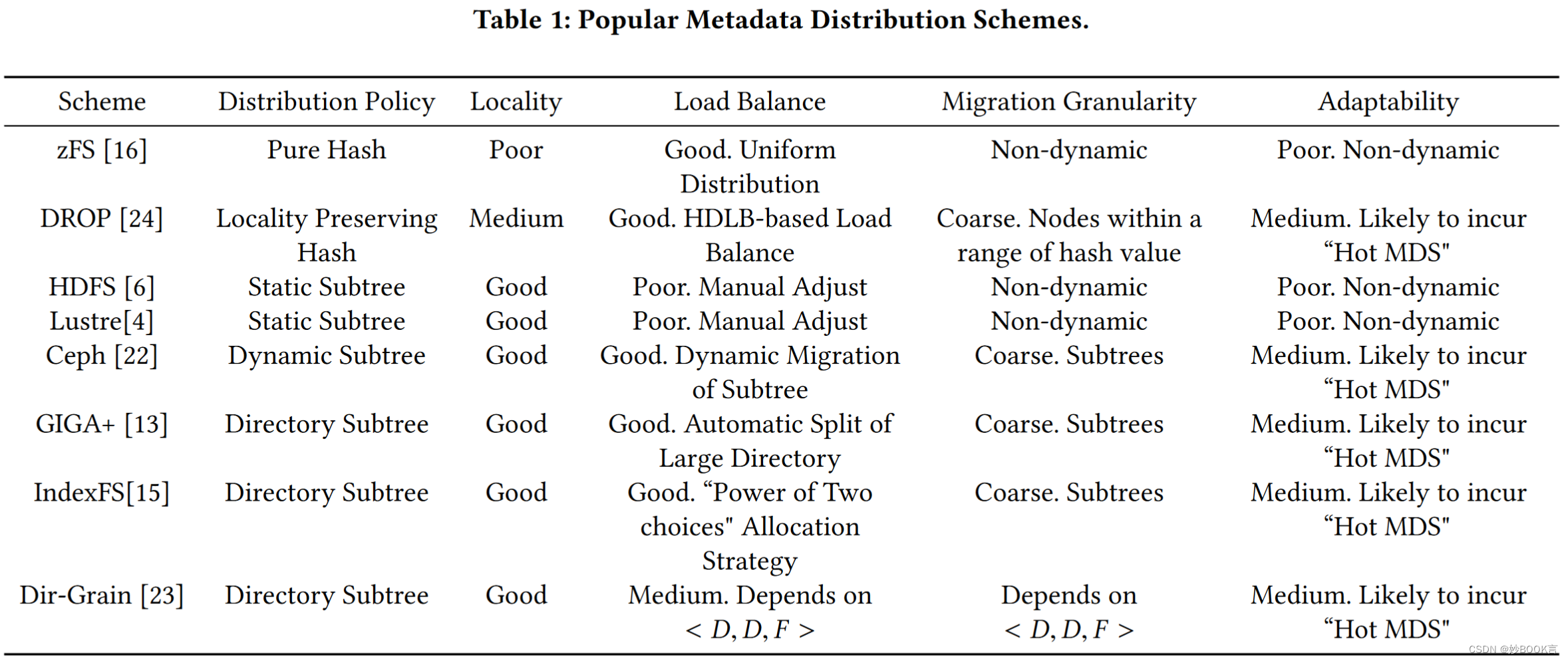
现有的方法采用基于历史的粗粒度方法,动态地将节点重新分配到不同的服务器,未能及时而有效地更新节点的分布。这种设计存在两个主要限制:第一,分布式更新基于定期的历史统计数据,因此会滞后于访问模式的变化;第二,粗粒度的迁移不可避免地会导致冗余的迁移成本,一些非热节点会频繁地与热节点一起移动,这也限制了性能的提高。
本文方法
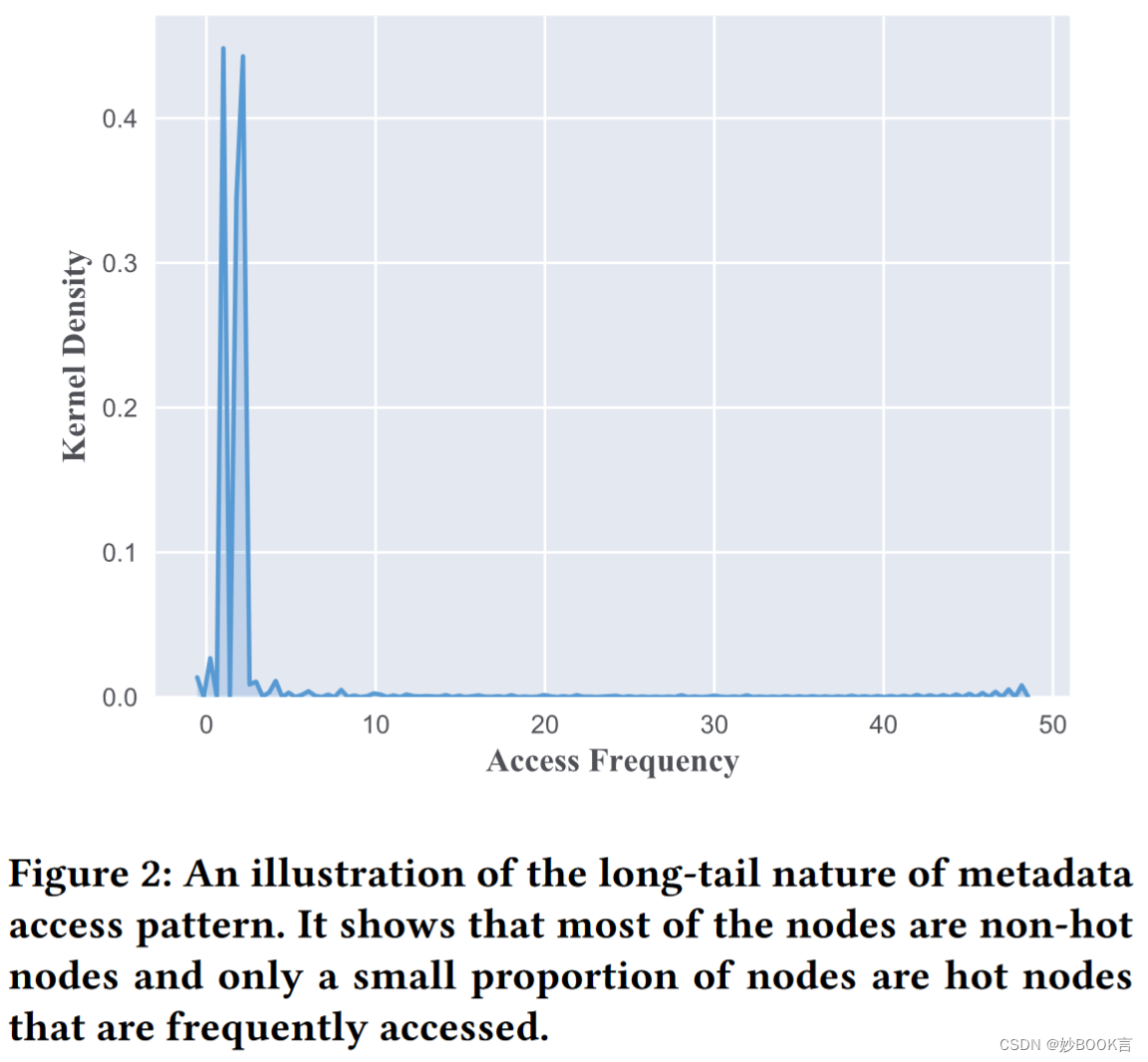
根据我们对元数据访问跟踪的分析,如图2所示,元数据访问模式具有长尾性质:大多数查询指向一小部分元数据(热节点)。基于这种特性,我们提出了细粒度迁移,该迁移作用于单个热节点,而不是子树或具有连续哈希值的一系列节点,以减少由非热节点的移动产生的不必要成本。
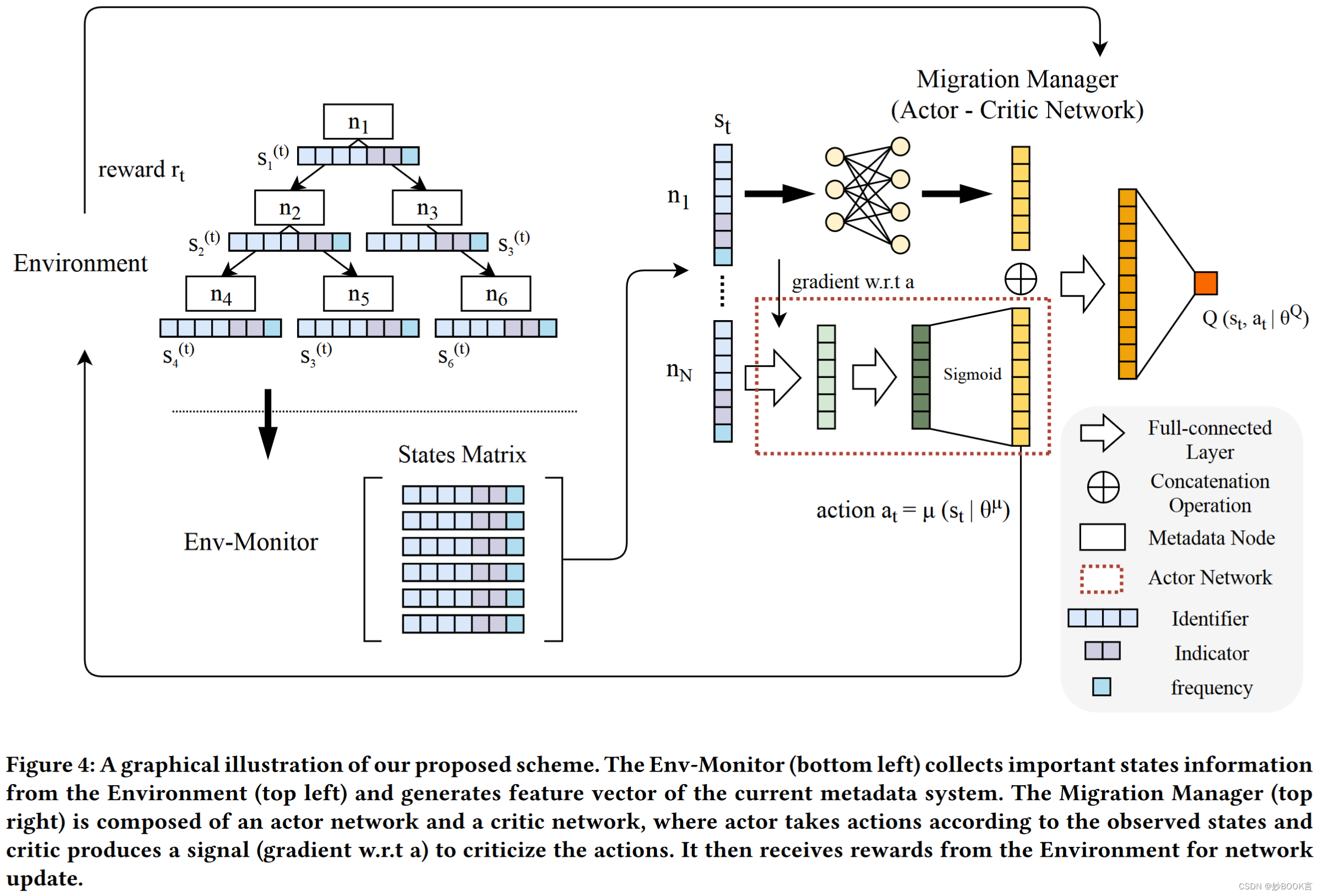
我们提出了一种自适应的细粒度元数据管理方案AdaM,利用深度强化学习来解决与时间变化的访问模式相对立的权衡困境。在每个时间步骤中,AdaM收集环境状态,包括:元数据节点在上一时间段的访问频率、MDS上节点的分布、名称空间树的结构。然后,利用训练的actor-critic网络,根据观察到的状态,将热元数据节点重新分配到不同的服务器。使用在下一个时间段完成所有访问后获得的奖励来更新网络,从而鼓励代理提前进行预测和采取行动,以适应访问模式的变化。对于变化的访问模式,AdaM能够动态地在不同的MDS上迁移热节点,以保持负载平衡并保持元数据的局部性。
我们在真实数据迹象上对AdaM进行了测试。实验结果表明我们提出的方法优于基于哈希[16],静态子树划分[25],动态子树划分[13],AngleCut[8]。
实验环境
LiveMap数据集 SNIA - Storage Networking Industry Association: IOTTA Repository Home,比较局部性、负载均衡度、访问分布、迁移开销、模型初始化影响
总结
为了同时解决元数据局部性和元数据服务器的负载均衡。作者认为之前的方法:基于历史数据,会滞后于访问模式的变化;迁移粒度太粗,导致冗余的迁移成本。提出基于深度强化学习(DRL)的细粒度迁移策略,根据DRL预测未来状态进行迁移,而且只迁移热节点,减少迁移开销。