IEEE754介绍
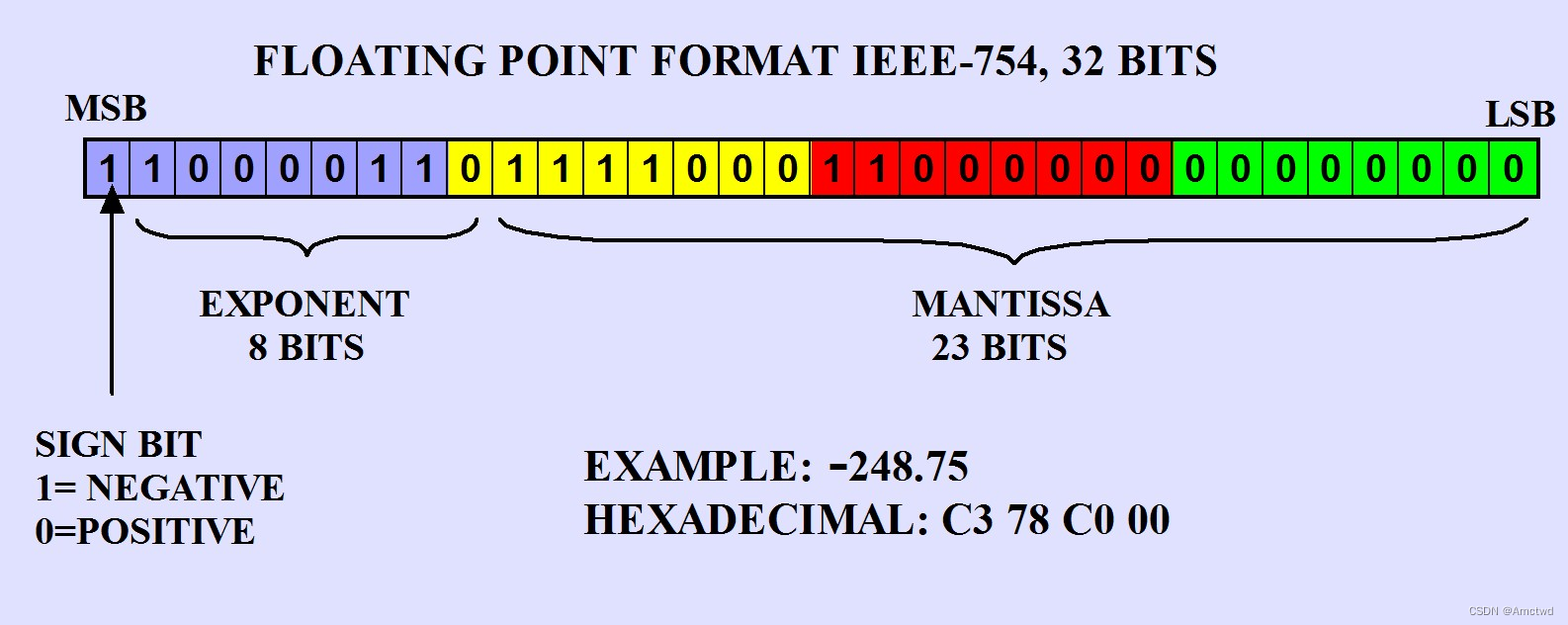
IEEE 754是一种标准,用于表示和执行浮点数运算的方法。在这个标准中,单精度浮点数使用32位二进制表示,分为三个部分:符号位、指数位和尾数位。
符号位(s)用一个位来表示数的正负,0表示正数,1表示负数。
指数位(e)用8位表示指数。对于单精度浮点数,指数位是以偏移量的形式表示的。也就是说,实际的指数值是指数位的无符号值减去一个偏移量(127)。
尾数位(m)用23位表示数的尾数部分。尾数是一个二进制小数,被规范化为一个小于1的数。
表达式:
V = ( − 1 ) s × ( 1. M ) × 2 ( E − 127 ) V = (-1)^s \times(1.M)\times 2^{(E-127)} V=(−1)s×(1.M)×2(E−127) (单精度)
V = ( − 1 ) s × ( 1. M ) × 2 ( E − 1023 ) V = (-1)^s \times(1.M)\times 2^{(E-1023)} V=(−1)s×(1.M)×2(E−1023)(双精度)
| IEEE 754 半精度浮点数 | 16 位 | 符号 1 位,指数 5 位,尾数 10 位 |
| IEEE 754 单精度浮点数 | 32 位 | 符号 1 位,指数 8 位,尾数 23 位 |
| IEEE 754 双精度浮点数 | 64 位 | 符号 1 位,指数 11 位,尾数 52 位 |
代码实现计算
我们首先定义了一个函数binaryIEEE754StringToFloat,它接收一个32位的二进制字符串作为输入,并返回一个浮点数。该函数首先确定输入字符串的长度,并在必要时进行填充,使其达到32位。
接下来,我们解析符号位、指数位和尾数位。符号位确定数的正负,指数位确定数的范围,尾数位确定数的精度。通过这些步骤,我们能够将二进制字符串转换为浮点数。
最后,我们在main函数中提供了一个示例二进制字符串,并调用binaryIEEE754StringToFloat函数进行转换。输出结果是一个浮点数,它就是我们所求的结果。
package main
import (
"fmt"
"math"
"strconv"
"strings"
)
func binaryIEEE754StringToFloat(binaryStr string) float32 {
n := 32 - len(binaryStr)
// 补充为32位
if n >= 0 && n < 32 {
binaryStr = strings.Repeat("0", n) + binaryStr
} else {
fmt.Println("二进制字符串的长度不合法")
return 0
}
// 解析符号位
sign := 1.0
if binaryStr[0] == '1' {
sign = -1.0
}
// 解析指数位
(exponent, _ := strconv.ParseInt(binaryStr[1:9], 2, 64))
(exponent -= 127)
// 解析尾数位
(mantissa := float32(0))
for i := 9; i < len(binaryStr); i++ {
if binaryStr[i] == '1' {
(mantissa += 1 / float32(math.Pow(2, float64(i-8))))
}
}
// 计算浮点数值
(result := float32(sign) * (1 + mantissa) * float32(math.Pow(2, float64(exponent))))
return result
}
func main() {
(binaryStr := "10111111100111101110101110000000") // 示例二进制字符串
(floatVal := binaryIEEE754StringToFloat(binaryStr))
fmt.Printf("转换后的浮点数为: %f\n", floatVal)
}
补充(Double类型转换):
func BinaryDoubleStringToFloat(binaryStr string) float64 {
// 补充为64位
n := 64 - len(binaryStr)
if n >= 0 && n < 64 {
binaryStr = strings.Repeat("0", n) + binaryStr
} else {
fmt.Println("二进制字符串的长度不合法")
return 0
}
// 解析符号位
sign := 1.0
if binaryStr[0] == '1' {
sign = -1.0
}
// 解析指数位
exponent, _ := strconv.ParseInt(binaryStr[1:12], 2, 64)
exponent -= 1023 // 双精度指数位的偏移量
// 解析尾数位
mantissa := float64(0)
for i := 12; i < len(binaryStr); i++ {
if binaryStr[i] == '1' {
mantissa += 1 / float64(math.Pow(2, float64(i-11)))
}
}
// 计算浮点数值
result := sign * (1 + mantissa) * math.Pow(2, float64(exponent))
return result
}