数组理论基础
文章链接:https://programmercarl.com/%E6%95%B0%E7%BB%84%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%80.html
977.有序数组的平方
题目链接:https://leetcode.cn/problems/squares-of-a-sorted-array/description/
思路1.暴力排序
将每个数平方之后,直接排序
class Solution {
public int[] sortedSquares(int[] nums) {
for(int i=0;i<nums.length;i++){
nums[i] = nums[i] * nums[i];
}
Arrays.sort(nums);
return nums;
}
}
时间复杂度 O(n + nlogn)
思路2.双指针法
注意这里数组是有序的,只不过在负数平方之后,有可能会变成最大数。
那么数组平方后的最大值,要么是在最左边,要么就是在最右边。
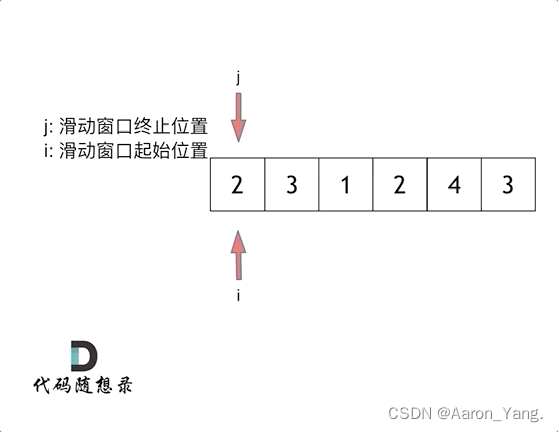
这里的话,我们就可以使用双指针,i指向起始位置,j指向终止位置。
然后,定义一个新的数组,和A数组同样的大小,让k指向result数组的终止位置(因为我们接收的数字是从大到小)
- 如果A[i] * A[i] < A[j] * A[j],那么result[k–] = A[j] * A[j];
- 如果A[i] * A[i] >= A[j] * A[j] 那么result[k–] = A[i] * A[i];
class Solution {
// 默认是有序的
public int[] sortedSquares(int[] nums) {
int i = 0;
int j = nums.length-1;
int[] result = new int[nums.length];
int k = j;
while(k>=0)
{
if(nums[i]*nums[i] >= nums[j]*nums[j]){
result[k--] = nums[i]*nums[i];
i++;
}
else{
result[k--] = nums[j]*nums[j];
j--;
}
}
return result;
}
}
时间复杂度 O(n),比暴力解法提升了很多
209.长度最小的子数组
题目连接:https://leetcode.cn/problems/minimum-size-subarray-sum/
解法1:暴力解法(遍历所有可能的子序列)
class Solution {
public:
int minSubArrayLen(int s, vector<int>& nums) {
int result = INT32_MAX; // 最终的结果
int sum = 0; // 子序列的数值之和
int subLength = 0; // 子序列的长度
for (int i = 0; i < nums.size(); i++) { // 设置子序列起点为i
sum = 0;
for (int j = i; j < nums.size(); j++) { // 设置子序列终止位置为j
sum += nums[j];
if (sum >= s) { // 一旦发现子序列和超过了s,更新result
subLength = j - i + 1; // 取子序列的长度
result = result < subLength ? result : subLength;
break; // 因为我们是找符合条件最短的子序列,所以一旦符合条件就break
}
}
}
// 如果result没有被赋值的话,就返回0,说明没有符合条件的子序列
return result == INT32_MAX ? 0 : result;
}
};
时间复杂度O(n^2)
解法2:滑动窗口
用一个for循环,如何表示滑动窗口的起始位置,还是终止位置。
假如我们用一个for循环,来表示滑动窗口的起始位置,那么遍历剩下的终止位置,又会陷入了暴力解法之中。
因此,这个循环的索引,只能是表示滑动窗口的终止位置。
那么,滑动窗口的起始位置如何移动,需要我们进行考虑。
具体见动画演示
class Solution {
public int minSubArrayLen(int target, int[] nums) {
int len = nums.length;
int i = 0;
int sum = 0;
int result = 9999999;
for(int j=0;j<len;j++){
sum = sum + nums[j];
while(sum>=target){
result = Math.min(result,j-i+1);
sum -= nums[i];
++i;
}
}
if(result==9999999) result = 0;
return result;
}
}
时间复杂度:O(n),不要以为for里放一个while就以为是O(n^2), 主要是看每一个元素被操作的次数,每个元素在滑动窗后进来操作一次,出去操作一次,每个元素都是被操作两次,所以时间复杂度是 2 × n 也就是O(n)。
#相关题目推荐
59.螺旋矩阵II
题目连接:https://leetcode.cn/problems/spiral-matrix-ii/
解法:模拟过程
本题并不涉及到什么算法,就是模拟过程,但却十分考察对代码的掌控能力。
求解本题依然是要坚持循环不变量原则。
我们模拟顺时针画矩阵的过程,由外向内一圈一圈的画下去,这里一圈下来,我们要画每四条边,这四条边怎么画,每画一条边都要坚持一致的左闭右开,或者左开右闭的原则,这样这一圈才能按照统一的规则画下来。
这里我们按照左闭右开的原则。
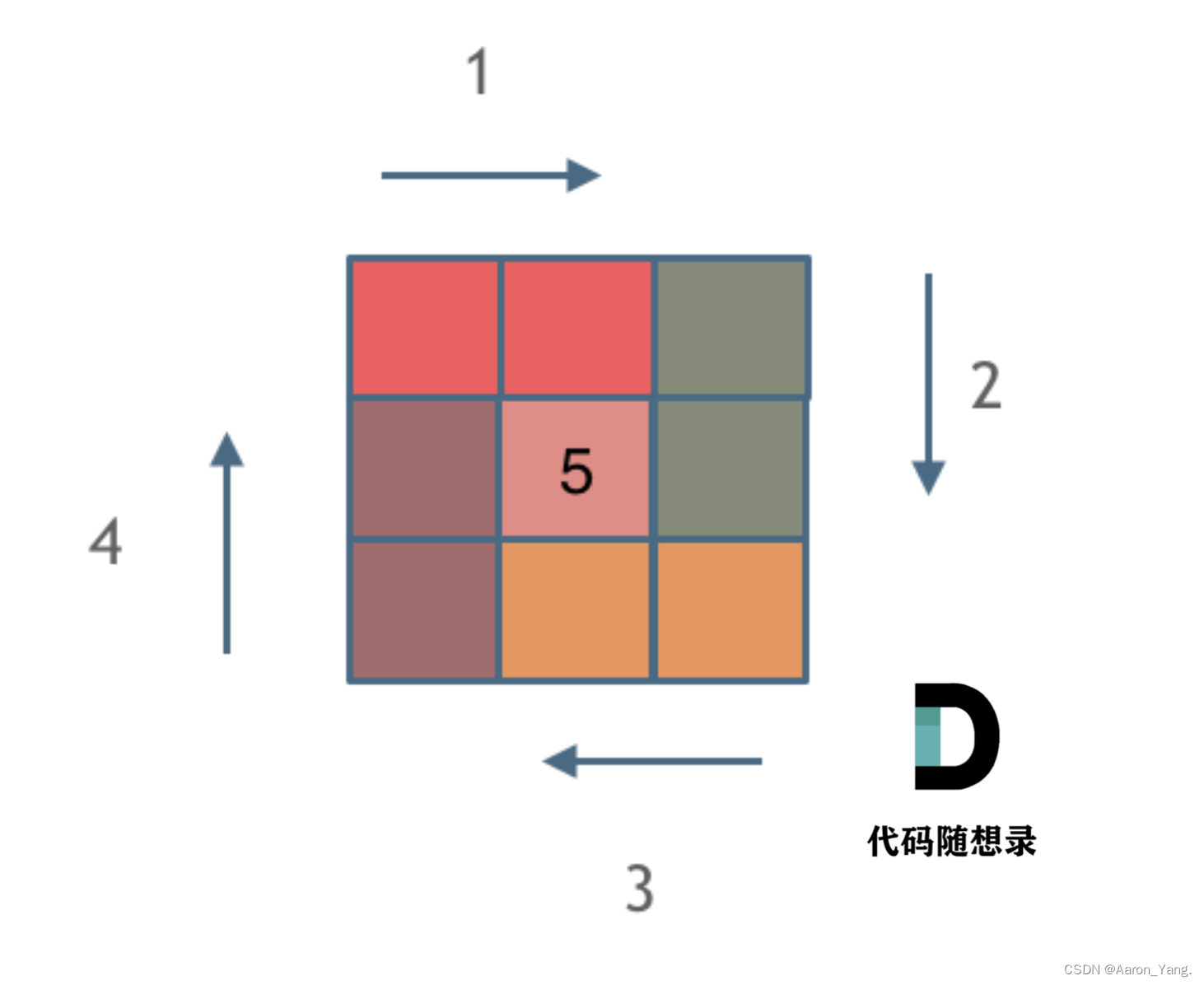
这里每一种颜色,代表一条边,我们遍历的长度,可以看出每一个拐角处的处理规则,拐角处让给新的一条边来继续画。
然后就是还要注意一个点,当n为奇数的时候,中间会多出一个方块,单独赋值即可。
class Solution {
public int[][] generateMatrix(int n) {
int[][] a = new int[n][n];
// 定义起始点
int startx = 0,starty=0;
// 循环次数
int loop = n/2;
int offset = 1;
int i,j;
int count = 1;
// 左闭右开的原则
while(loop-- > 0)
{
i=startx;j=starty;
// 最上面
for(j=starty;j<n-offset;j++){
a[i][j] = count++;
}
// 右边(此时i=n-offset了)
for(i=startx;i<n-offset;i++){
a[i][j] = count++;
}
// 下边(此时i,j在最下角)
for(;j>starty;j--)
a[i][j] = count++;
for(;i>startx;i--)
a[i][j] = count++;
// 第二圈开始的时候,起始位置要各自加1, 例如:第一圈起始位置是(0, 0),第二圈起始位置是(1, 1)
++startx;
++starty;
// 控制每一圈里遍历的长度,例如第一圈是n-1,第二圈就是n-2
++offset;
}
if(n%2!=0)
a[n/2][n/2] = count;
return a;
}
}
时间复杂度:O(n^2)
空间复杂度:O(1)