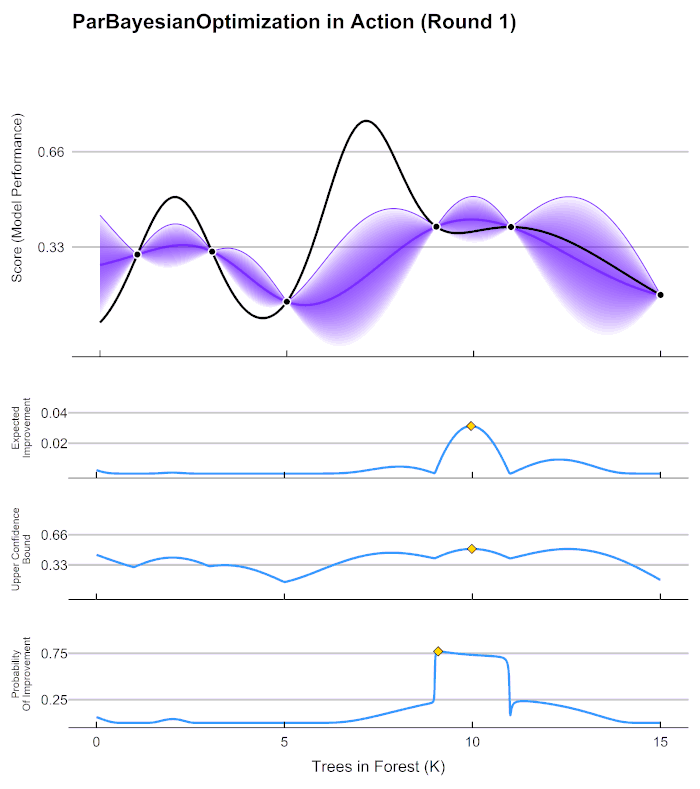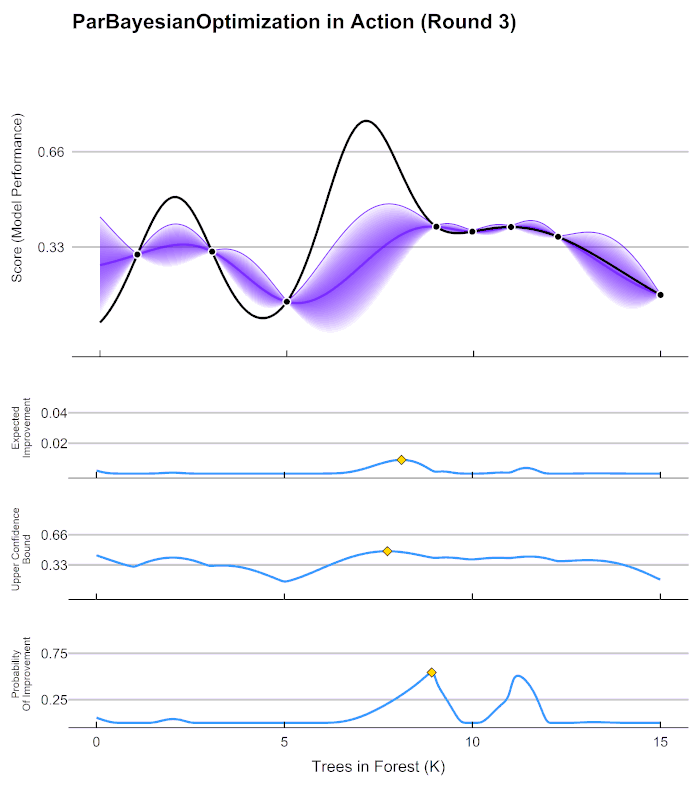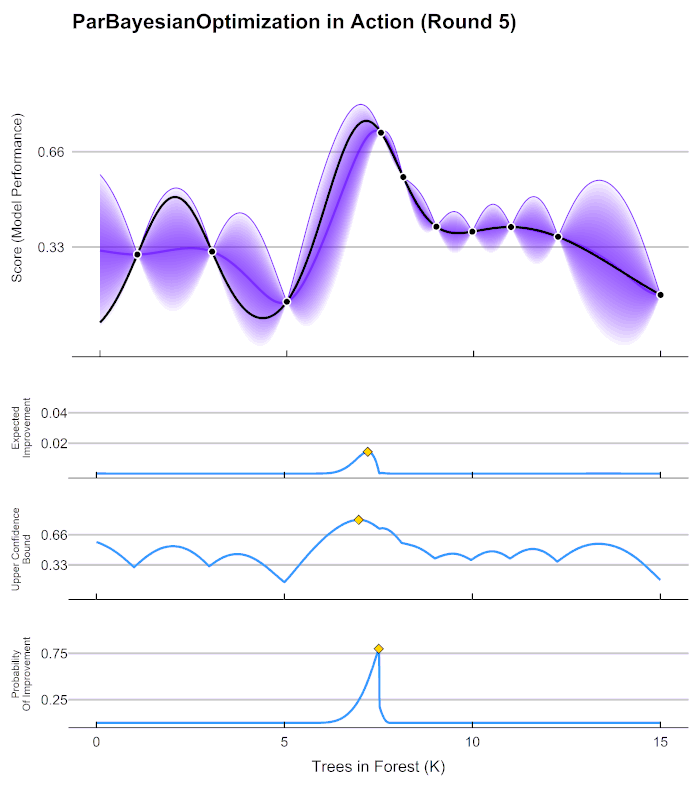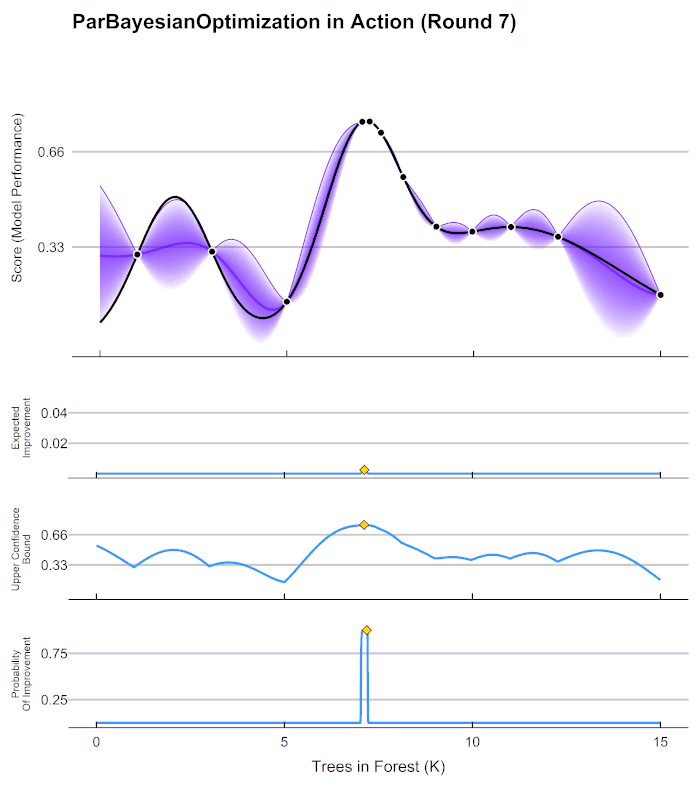
贝叶斯优化的基本流程

假设已知一个函数𝑓(𝑥)的表达式以及其自变量𝑥的定义域，现在，我们希望求解出𝑥的取值范围上𝑓(𝑥)的最小值，你打算如何求解这个最小值呢？
1 我们可以对𝑓(𝑥)求导、令其一阶导数为0来求解其最小值
函数𝑓(𝑥)可微，且微分方程可以直接被求解
2 我们可以通过梯度下降等优化方法迭代出𝑓(𝑥)的最小值
函数𝑓(𝑥)可微，且函数本身为凸函数
3 我们将全域的𝑥带入𝑓(𝑥)计算出所有可能的结果，再找出最小值
函数𝑓(𝑥)相对不复杂、自变量维度相对低、计算量可以承受

假设现在函数𝑓(𝑥)是一个平滑均匀的函数，但它异常复杂、且不可微，我们无法使用上述三种方法中的任意一种方法求解，但我们还是想求解其最小值，可以怎么办呢？由于函数异常复杂，带入任意𝑥计算的所需的时间很长，所以我们不太可能将全域𝑥都带入进行计算，但我们还是可以从中随机抽样部分观测点来观察整个函数可能存在的趋势。于是我们选择在𝑥的定义域上随机选择了4个点，并将4个点带入𝑓(𝑥)进行计算，得到了如下结果：

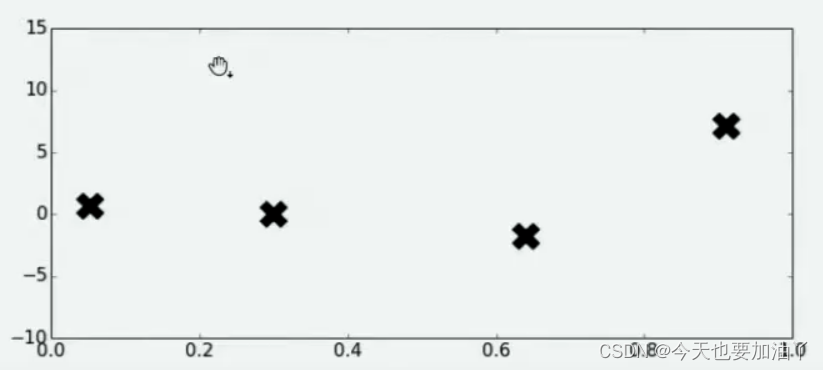
好了，现在有了这4个观测值，你能告诉我𝑓(𝑥)的最小值在哪里吗？你认为最小值点可能在哪里呢？大部分人会倾向于认为，最小值点可能非常接近于已观测出4个𝑓(𝑥)值中最小的那个值，但也有许多人不这么认为。当我们有了4个观测值，并且知道我们的函数时相对均匀、平滑的函数，那我们可能对函数的整体分布有如下猜测：

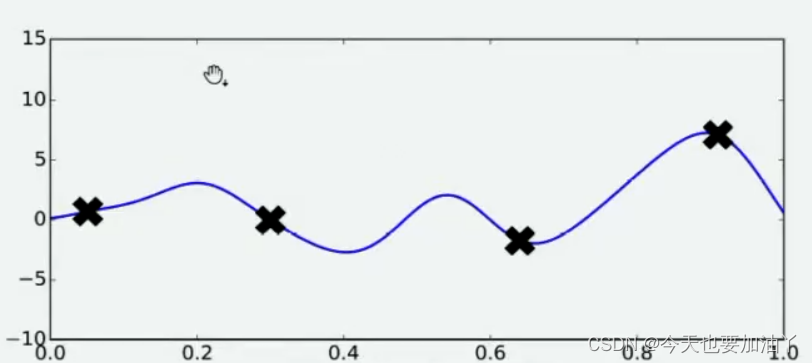
当我们对函数整体分布有一个猜测时，这个分布上一定会存在该函数的最小值。同时，不同的人可能对函数的整体分布有不同的猜测，不同猜测下对应的最小值也是不同的。


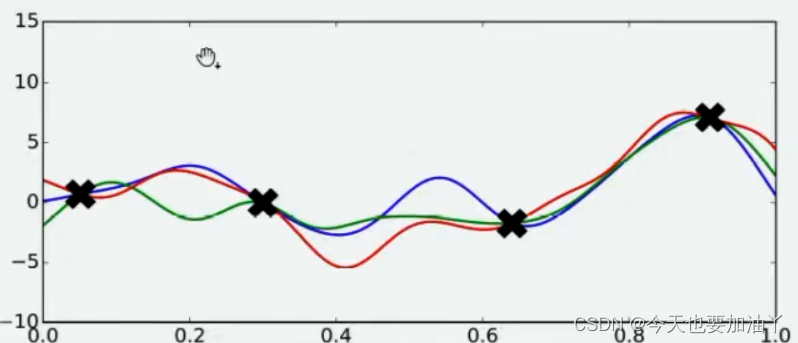
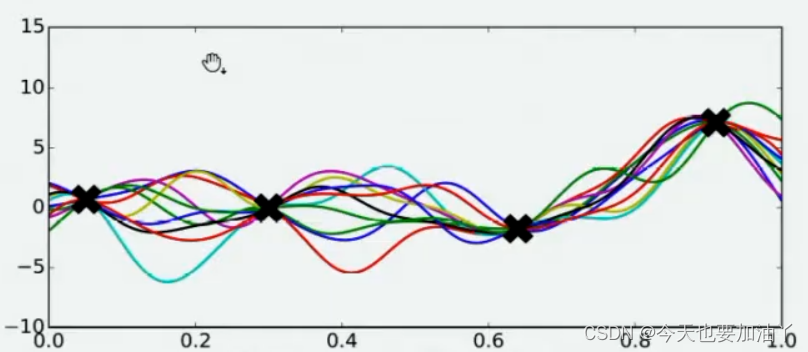
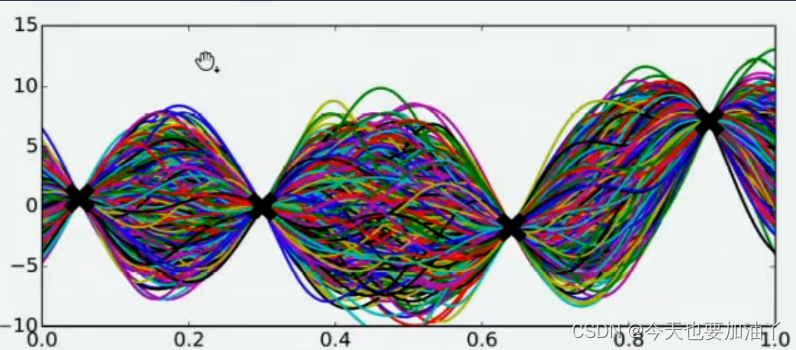
现在，假设我们邀请了数万个人对该问题做出猜测，每个人所猜测的曲线如下图所示。不难发现，在观测点的附近，每个人猜测的函数值差距不大，但是在远离远侧点的地方，每个人猜测的函数值就高度不一致了。这也是当然的，因为观测点之间函数的分布如何完全是未知的，并且该分布离观测点越远时，我们越不确定真正的函数值在哪里，因此人们猜测的函数值的范围非常巨大。

现在，我们将所有猜测求均值，并将任意均值周围的潜在函数值所在的区域用色块表示，可以得到一条所有人猜测的平均曲线。不难发现，色块所覆盖的范围其实就是大家猜测的函数值的上界和下界，而任意𝑥所对应的上下界差异越大，表示人们对函数上该位置的猜测值的越不确定。因此上下界差异可以衡量人们对该观测点的置信度，色块范围越大，置信度越低。

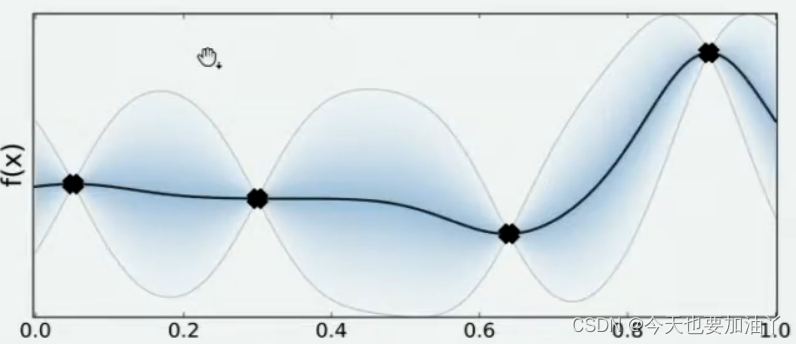
在观测点周围，置信度总是很高的，远离观测点的地方，置信度总是很低，所以如果我们能够在置信度很低的地方补充一个实际的观测点，我们就可以很快将众人的猜测统一起来。以下图为例，当我们在置信度很低的区间内取一个实际观测值时，围绕该区间的“猜测”会立刻变得集中，该区间内的置信度会大幅升高。

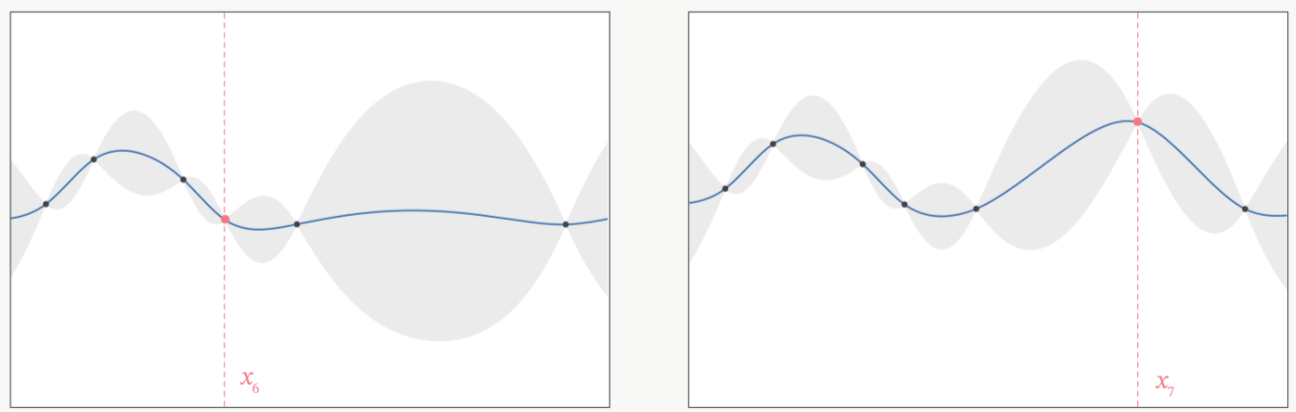
当整个函数上的置信度都非常高时，我们可以说我们得出了一条与真实的$f(x)$曲线高度相似的曲线$f^{\ast }$，次数我们就可以将$f^{\ast }$的最小值当作真实$f(x)$的最小值来看待。自然，如果估计越准确，$f^{\ast }$越接近$f(x)$，则$f^{\ast }$的最小值也会越接近于$f(x)$的真实最小值。那如何才能够让$f^{\ast }$更接近$f(x)$呢？根据我们刚才提升置信度的过程，很明显——观测点越多，我们估计出的曲线会越接近真实的$f(x)$。然而，由于计算量有限，我们每次进行观测时都要非常谨慎地选择观测点。那现在，如何选择观测点才能够最大程度地帮助我们估计出$f(x)$的最小值呢？

有非常多的方法，其中最简单的手段是使用最小值出现的频数进行判断。由于不同的人对函数的整体分布有不同的猜测，不同猜测下对应的最小值也是不同的，根据每个人猜测的函数结果，我们在$X$轴上将定义域区间均匀划分为100个小区间，如果有某个猜测的最小值落在其中一个区间中，我们就对该区间进行计数（这个过程跟对离散型变量绘制直方图的过程完全一致）。当有数万个人进行猜测之后，我们同时也绘制了基于$X$轴上不同区间的频数图，频数越高，说明猜测最小值在该区间内的人越多，反之则说明该猜测最小值在该区间内的人越少。该频数一定程度上反馈出最小值出现的概率，频数越高的区间，函数真正的最小值出现的概率越高。

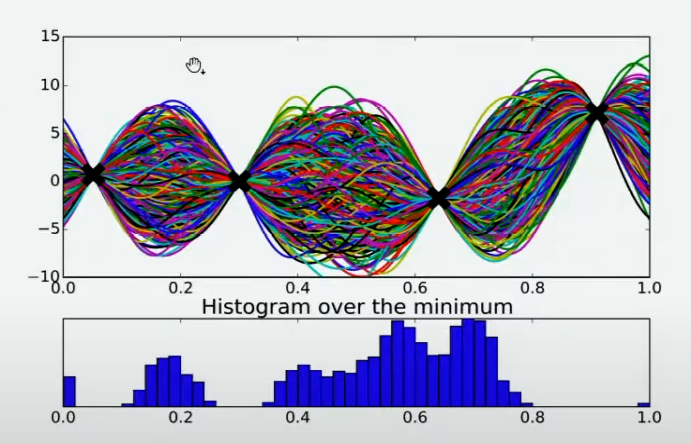
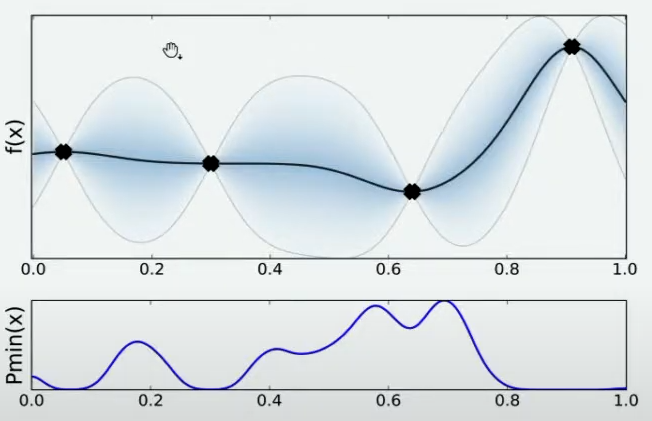
当我们将$X$轴上的区间划分得足够细后，绘制出的频数图可以变成概率密度曲线，曲线的最大值所对应的点是$f(x)$的最小值的概率最高，因此很明显，我们应该将曲线最大值所对应的点确认为下一个观测点。根据图像，我们知道最小值最有可能在的区间就在x=0.7左右的位置。当我们不取新的观测点时，现在$f(x)$上可以获得的可靠的最小值就是x=0.6时的点，但我们如果在x=0.7处取新的观测值，我们就很有可能找到比当前x=0.6的点还要小的$f_{min}$。因此，我们可以就此决定，在x=0.7处进行观测。

当我们在x=0.7处取出观测值之后，我们就有了5个已知的观测点。现在，我们再让数万人根据5个已知的观测点对整体函数分布进行猜测，猜测完毕之后再计算当前最小值频数最高的区间，然后再取新的观测点对$f(x)$进行计算。当允许的计算次数被用完之后（比如，500次），整个估计也就停止了。

你发现了吗？在这个过程当中，我们其实在不断地优化我们对目标函数$f(x)$的估计，虽然没有对$f(x)$进行全部定义域上的计算，也没有找到最终确定一定是$f(x)$分布的曲线，但是随着我们观测的点越来越多，我们对函数的估计是越来越准确的，因此也有越来越大的可能性可以估计出$f(x)$真正的最小值。这个优化的过程，就是贝叶斯优化。