《堆排序》与《Top

《堆排序》与《Top—k》

news2024/11/19 19:18:56

编辑

前言：

关于《堆排序》：

第一步：建堆

第二步：排序

《Top—K问题》

关于Top—k问题：

前言：

我们在前面的blog中，对于《堆》已经有了初步的概念，那么接下来我们可以利用《堆》来解决我们日常生活中存在的问题，本篇我们给出两个常用的应用场景，分别是《排序》以及《Top—k问题》，上一篇blog在：《堆》的模拟实现-CSDN博客

关于《堆排序》：

#define _CRT_SECURE_NO_WARNINGS  1
#include<stdio.h>

void swap(int* a, int* b)
{
	int tmp = *a;
	*a = *b;
	*b = tmp;
}

void AdjustDown(int* arr, int sz, int parent)
{
	int child = parent * 2 + 1;
	while (child < sz)
	{
		if (child + 1 < sz && arr[child] < arr[child + 1])
		{
			child++;
		}

		if (arr[child] > arr[parent])
		{
			swap(&arr[child], &arr[parent]);
			parent = child;
			child = 2 * parent + 1;
		}
		else
		{
			break;
		}
	}
}

void AdjustUp(int* arr, int sz, int child)
{
	while (child > 0)
	{
		int parent = (child - 1) / 2;
		if (arr[parent] < arr[child])
		{
			swap(&arr[parent], &arr[child]);
		}
		child = parent;
	}
}

int main()
{
	int arr[] = { 2, 6, 9, 3, 1, 7 };
	int sz = sizeof(arr) / sizeof(arr[0]);
	for (int i = (sz - 1 - 1) / 2; i >= 0; i--)
	{
		AdjustDown(arr, sz, i);
	}//向下调整算法
	

	//for (int i = 1; i<sz; i++)
	//{
	//	AdjustUp(arr, sz, i);
	//}//向上调整算法

	int end = sz - 1;
	while (end > 0)
	{
		swap(&arr[0], &arr[end]);
		AdjustDown(arr, end, 0);
		--end;
	}
	return 0;
}

第一步：建堆

利用《堆》可以方便我们对一个给定的乱序数组实现排序，首先我们应当选择大堆来进行排序操作。

为什么我们不选择使用小堆来进行建堆呢？

通过之前对《堆》的blog说明，小堆就是对顶元素为最小元素，其他的节点数都比第一个元素小，那么如果是小堆，最小的数字已经就是第一个元素，若要找出次小的元素，则又需要在剩下的元素中再进行建堆，重复循环才能完成排序，这样子的时间复杂度高，不利于排序。

因此我们选择利用大堆来建堆，实现大堆后，再将首尾的元素进行交换，再利用向下调整法调整法对剩下的n-1个元素进行调整，再进行交换，如此能实现排序。

    int arr[] = { 2, 6, 9, 3, 1, 7 };
	int sz = sizeof(arr) / sizeof(arr[0]);

	for (int i = 1; i<sz; i++)
	{
	   AdjustUp(arr, sz, i);
	}

对如图的数组进行向上调整法建堆：

第二步：排序

首先我们将首尾元素进行交换：

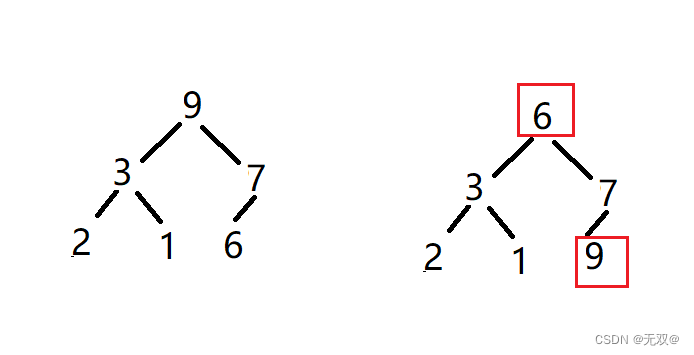
对除最后一个元素外的其他元素进行向下调整法，将其继续成大堆

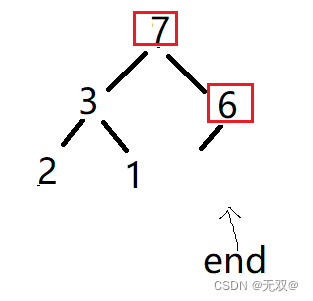
重复上述步骤

最终可得堆为：

如此则完成了堆排序。

《Top—K问题》

关于Top—k问题：

即求数据结合中前K个最大的元素或者最小的元素，一般情况下数据量都比较大。

比如：专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。我们以求n个数据中前K个最大的元素为例进行说明：(假设n=10000) (假设k=10)

#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<stdlib.h>
#include<time.h>
const char* file = "data.txt";
void swap(int* a, int* b)
{
	int tmp = *a;
	*a = *b;
	*b = tmp;
}

void AdjustDown(int* arr, int sz, int parent)
{
	int child = 2 * parent + 1;
	while (child < sz)
	{
		if (child + 1 < sz && arr[child + 1] < arr[child])
		{
			child++;
		}

		if (arr[child] < arr[parent])
		{
			swap(&arr[child], &arr[parent]);
			parent = child;
			child = 2 * parent + 1;
		}
		else
		{
			break;
		}
	}
}

void CreateFile()
{
	//创建随机数的种子
	srand((unsigned int)time(NULL));
	FILE* Fin = fopen(file, "w");
	if (Fin == NULL)
	{
		perror("Fopen error");
		exit(-1);
	}

	int n = 10000000;
	for (int i = 0; i < n; i++)
	{
		int x = (rand() + i) % n;
		fprintf(Fin, "%d\n", x);
	}

	fclose(Fin);
	Fin = NULL;
}

void Print()
{
	FILE* Fout = fopen(file, "r");
	if (Fout == NULL)
	{
		perror("Fout error");
		exit(-1);
	}

	//取前k个数进小堆
	int* minheap = (int*)malloc(sizeof(int) * 5);
	if (minheap == NULL)
	{
		perror("minheap -> malloc");
		return;
	}


	for (int i = 0; i < 5; i++)
	{
		fscanf(Fout, "%d", &minheap[i]);
	}

	for (int i = (5-1-1)/2; i >=0; --i)
	{
		AdjustDown(minheap, 5, i);
	}

	//读取数据
	int x = 0;
	while (fscanf(Fout, "%d", &x) != EOF)
	{
		if (minheap[0] < x)
		{
			minheap[0] = x;
		}
		AdjustDown(minheap, 5, 0);
	}

	for (int i = 0; i < 5; i++)
	{
		printf("%d ", minheap[i]);
	}

	fclose(Fout);
	Fout = NULL;
}

int main()
{
	//CreateFile();
	Print();
	return 0;
}

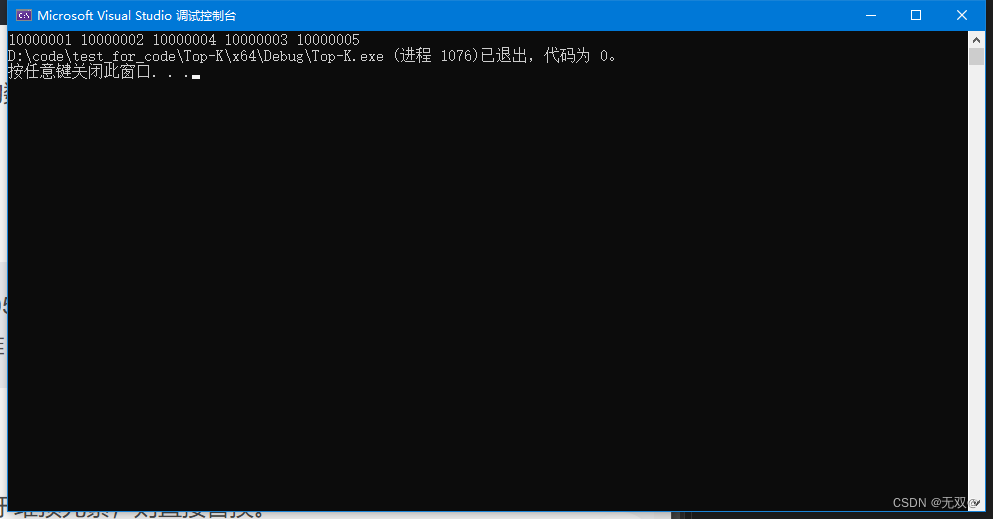
首先我们先创建10000000个随机数，再对其中的数字进行修改，随机抽5个数，分别修改为

10000001，10000002，10000003，10000004，10000005

再建一个小堆，注意，这里一定是小堆！