先回顾调制的过程:调制就是对信号源的信息进行处理加到载波上,使其变为适合于信道传输的形式的过程,就是使载波随信号而改变的技术。
1.什么是IQ调制?
答:将数据分为两路,分别进行载波调制,两路载波信号互相正交,I路载波为cos(in-phase,同相),Q路载波为sin(quadrature,正交),两路信号正交,频谱利用率是单项调制的两倍。
2.如何将调制信号波形表示为适量空间的一个点?
答:调制将不同的比特信息映射为有线信号波形集合S={s1(t),s2(t)....,sM(t)}终端特定波形,每个调制波形sm(t)都可表示为适量空间中的一个点
m=1,2,3,...,M
其中为坐标轴(归一化正交基信号),x的各个值为其坐标值。
3.为什么在衰落信道中需要使用分集技术,可以采用直接提升发送功率的方法吗?
答:衰落信道中可能出现深衰落现象,采用分集技术增加收发两端间传输信号的支路数量(各支路不相关),增加信号经过良好支路的概率,提高接收信号总信噪比,降低系统信号传输的误码率;
直接提升发送功率抗深衰落性能比分集差,但不采用。提升功率所能达到性能效率比分集低(信号发送功率相同,但分集误码率下降更多),硬件实现难度大(功放线性区间有限制)。
4.给出EGC和SC的中英文全称,各自的基本原理分别是什么?
答:EGC(equalgain combining,等增益合并):先对所有分集支路信号进行同相(相位偏移纠正),后对各支路信号进行等权重叠加;
SC(selection combining,选择性合并):对比所有的分集支路信号,选择幅度或SNR最大的支路信号进行解调和检测。
5.给出MRC的中英文全称,MRC的加权系数如何设置?为什么?
答:MRC(maximalratio combining,最大比合并): 对所有M条分集支路信号进行加权叠加,且Kth支路信号的权重Ak为各支路信号电压与噪声功率之比;
叠加后的检测信号的信噪比:
当且仅当等号成立时,Kth支路信噪比为单支路信噪比。
6.结合平均信噪比公式,说明为什么分集可以改进BER性能,性能的改进与哪个分集参数密切相关?
答:公式中给定信道gk时,单个检测信号SNR可得,对多条支路信号求和,检测信号SNR增加,分集可提高担心好的信噪比,降低BER;
系统改进与分集支路数M和单支路信噪比期望有关,当但之路信噪比期望大于等于零时,仅与M相关,且存在误码平底。
7.什么是信道编码?为什么需要信道编码?
答:在信息序列中加入冗余,对序列引入逻辑关系。即使接收到错误序列,接收端仍能利用编码规律尽可能纠正错误,恢复正确发送序列;信道中噪声、干扰和衰落等因素使接收端误码率降低,难以达到满足移动通信终端应用需求。引入信道编码能降低系统误码率,提升传输可靠性。
8.常用信道编码:分组码(2G,3G,4G);
循环校验码:CRC (2G,3G,4G);
卷积码convolutional code(2G,3G,4G);
Turbo Code(3G,4G);
LDPC(5G);
极化码 polar code (5G);
9.信道编码是数字通信系统纠错技术的核心
FEC前向纠错(单工连接):使用传输码字中的几余来检测和校正在传输期间产生的错误;
ARQ自动重传请求(全双工连接):仅将余用于错误检测。接收方向发送方发送一个反馈,说明是否在接收到的数据包中检测到任何错误(分别为不确认 (NACK)和确认 (ACK))。如果发射机接收到NACK,则重传先前发送的分组;
混合ARQ(ARQ+FEC):全双工连接;错误检测和校正。
10.分组码:(n,k)分组码
信息流由k个元素的块组成;每个块被映射到一个更大的n个元素的块,称为码字。
冗余字符:n-k;
码率:R=k/n;
例如n=6,k=3,码率=3/6=0.5
(100)——>(110100);
分组码可分为线性分组码和非线性分组码;
11.线性分组码中有一个重要参数,汉明重量W,为其中非零元素的个数,两个码字之间的汉明距离则是两个码字之间的不同元素数。
线性分组码的检错能力e=dmin-1;纠错能力t=[(dmin-1)/2];
12.什么是线性分组码?线性组码有什么特征?
答:在一个(n,k)分组码中,任意选择两个码字Ci和Cj和两个信息位字母表数值am和an,若am*Ci+an*Cj仍为该分组码中的码字,则该分组码为线性分组码;
线性分组码中必须包含全零的码字;
13.C=mG,G则为生成矩阵;

系统分组码与非系统分组码并无本质区别;非系统分组码的生成矩阵可以通过行初等变换转换为系统形式,这个过程称为系统化;系统化并不改变码集,其纠错能力完全等价;

14.H称为奇偶检验矩阵,它的行是线性无关的,奇偶校验矩阵。

任意非零码字C与奇偶检验矩阵之间的关系如下:

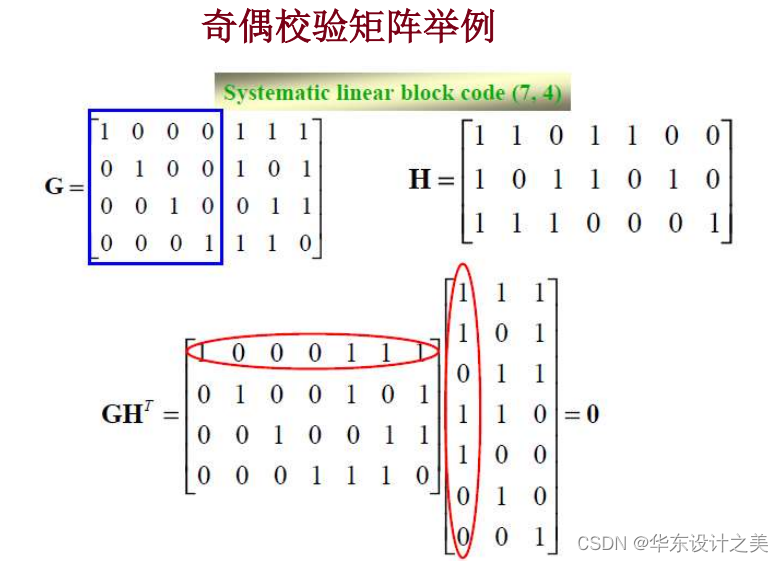
15.汉明码:汉明码是线性分组码的一个子类,属于完全码的范畴;
汉明码表示为单个整数m>=2的函数,