目录
1.程序功能描述
2.测试软件版本以及运行结果展示
3.核心程序
4.本算法原理
4.1 编码与初始化
4.2 适应度函数
4.3 遗传操作
4.4 自适应机制
4.5 终止条件
5.完整程序
1.程序功能描述
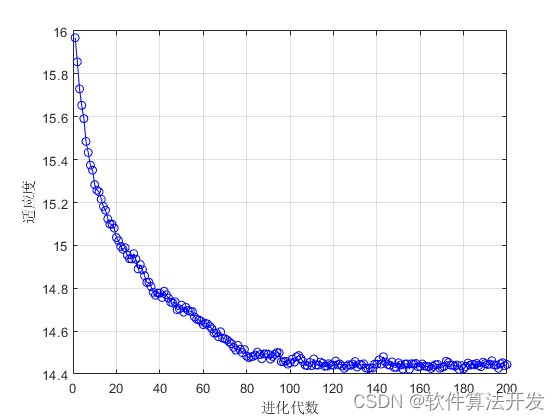
基于自适应遗传算法的车间调度matlab仿真,可以任意调整工件数和机器数,输出甘特图和优化算法的适应度收敛曲线。
2.测试软件版本以及运行结果展示
MATLAB2022a版本运行
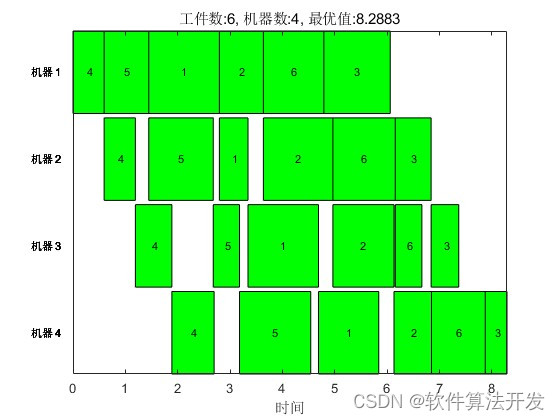
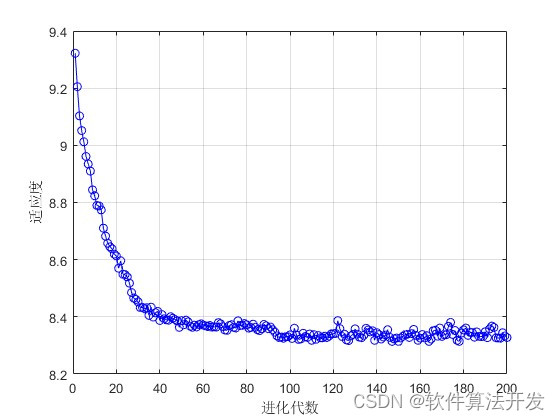
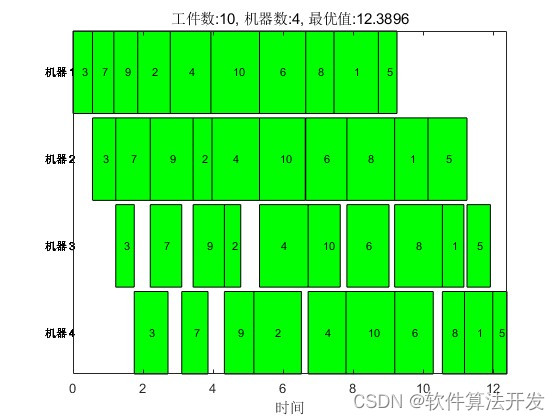

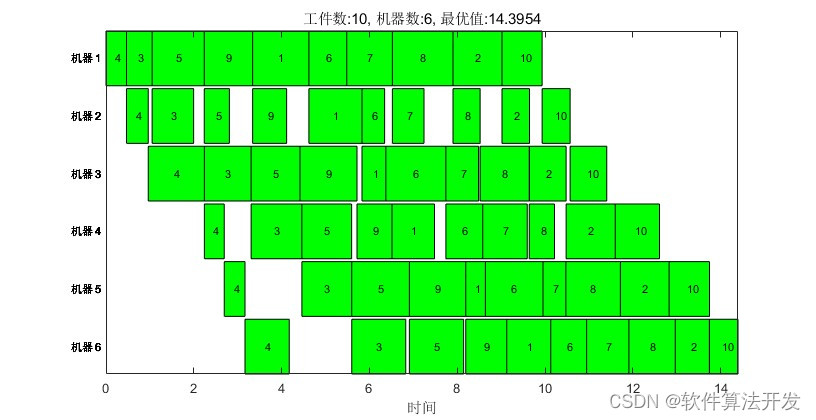
3.核心程序
........................................................
%工件数
Num1 = 8;
%机器数
Num2 = 2;
%产生时间矩阵
T = 0.4+rand(Num2,Num1);
%种群
Npop = 100;
%最大进化代数
Iters= 200;
%初始种群
Pop_n = round(sqrt(Npop));
Pop_s = ceil(Npop/Pop_n);
Npop = Pop_s*Pop_n;
[Xs,ff] = func_initial(T,Npop);
fout = zeros(Iters,1);
for i = 1:Iters
i
[ff,I] = sort(ff,'descend');
Xs = Xs(I,:);
Pmax = Xs(1,:);
Fmax = ff(1);
for j = 1:Pop_n
%子种群
Pops = Xs(j:Pop_n:end,:);
ff_ = ff(j:Pop_n:end,:);
[Popss,F3] = func_GA(T,Pops,ff_,Pmax,Fmax);
Xs(j:Pop_n:end,:) = Popss;
ff(j:Pop_n:end,:) = F3;
end
%进化
[Xsolve,ybest] = func_Eval(Xs,ff);
fout(i) = -ybest;
end
[Fouts,Etime] = func_fitness(T,Xsolve);
figure
%开始
Stime = Etime-T(:,Xsolve);
fval = -Fouts;
M1 = size(T,1); %机器数
NX = length(Xsolve); %工件数
figure;
plot(1:Iters,fout(1:end),'b-o');
grid on;
xlabel('进化代数');
ylabel('适应度');
194.本算法原理
车间调度问题是一类典型的组合优化问题,旨在确定一组工件在一组机器上的加工顺序,以优化某些性能指标,如最小化完工时间、延迟时间等。自适应遗传算法(Adaptive Genetic Algorithm, AGA)是一种启发式搜索算法,通过模拟生物进化过程中的遗传、变异、选择和自然选择等机制来求解优化问题。
4.1 编码与初始化
在自适应遗传算法中,首先需要定义一种编码方式来表示问题的解。对于车间调度问题,通常采用基于工件的编码方式,即每个基因代表一个工件,基因的顺序代表工件的加工顺序。然后,随机生成一组初始解作为初始种群。
4.2 适应度函数
适应度函数用于评价每个解的质量。对于车间调度问题,适应度函数通常与要优化的性能指标相关。例如,如果要最小化完工时间,适应度函数可以是完工时间的倒数,或者直接使用完工时间的负值。
4.3 遗传操作
遗传操作包括选择、交叉和变异。选择操作根据每个解的适应度值选择优秀的解进入下一代。交叉操作通过交换两个解的部分基因来生成新的解。变异操作通过随机改变某个解的一个或多个基因来引入新的多样性。
选择操作:常见的选择策略有轮盘赌选择、锦标赛选择等。以轮盘赌选择为例,每个解被选中的概率与其适应度值成正比。
交叉操作:对于基于工件的编码方式,可以采用如顺序交叉(Order Crossover, OX)、部分匹配交叉(Partially Matched Crossover, PMX)等交叉方法。
变异操作:常见的变异操作包括交换变异、插入变异等。
4.4 自适应机制
自适应遗传算法的关键在于其自适应机制,即算法能够根据种群的进化状态动态调整遗传操作的参数,如交叉概率、变异概率等。这种自适应机制有助于提高算法的搜索效率和全局寻优能力。
4.5 终止条件
算法终止条件可以是达到最大迭代次数、解的质量满足要求、种群多样性低于阈值等。
5.完整程序
VVV