「前言」文章内容是排序算法之选择排序的讲解。（所有文章已经分类好，放心食用）

「归属专栏」排序算法

「主页链接」个人主页

「笔者」枫叶先生(fy)

选择排序

1.1 原理

选择排序是一种简单直观的排序算法

它的工作原理是：

• 每一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置
• 然后再从剩余的未排序元素中继续寻找最小（或最大）的元素，依次类推，直到所有元素排序完毕

选择排序：基于数组（顺序表）的结构进行排序

例如

原始数组如下，使用选择排序进行排序，选最小元素进行交换（升序）

遍历第一趟数组，找出数组的最小值，与第一个数据交换

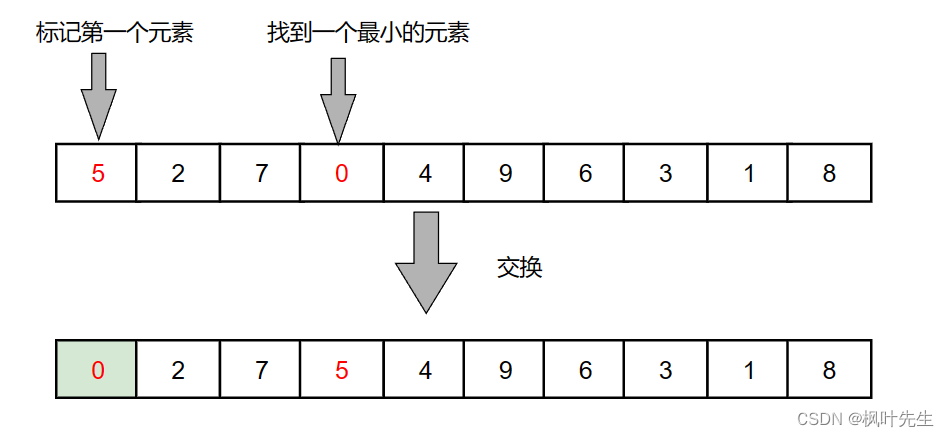
遍历第二趟数组，继续找出最小值，与第二个数据交换

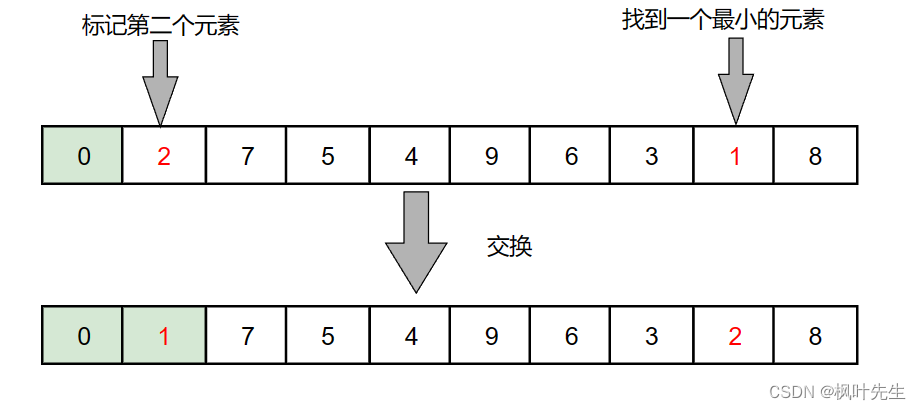
重复上述动作，直到数组有序

动图演示：（下列是选最小）

1.2 代码实现（C/C++）

C语言代码如下：（升序）

void Swap(int* p1, int* p2)
{
	int tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}

// 选择排序（以下代码是选最小）
void SelectSort(int* arr, int n)
{
	for (int i = 0; i < n; ++i)
	{
		int min = i; // 记录最小值元素的下标
		int start = i + 1;
		while (start < n)
		{
			if (arr[start] < arr[min]) min = start; // 最小值的下标更新
			++start;
		}
		Swap(&arr[i], &arr[min]); // 交换两个元素
	}
}

C++代码：（升序）

// 选择排序（以下代码是选最小）
void SelectSort(vector<int>& arr)
{
	int n = arr.size();
	for (int i = 0; i < n; ++i)
	{
		int min = i; // 记录最小值元素的下标
		int start = i + 1;
		while (start < n)
		{
			if (arr[start] < arr[min]) min = start; // 最小值的下标更新
			++start;
		}
		swap(arr[i], arr[min]); // 交换
	}
}

1.3 优化

实际上，我们可以一趟选出两个值，一个最大值一个最小值，然后将其放在序列开头和末尾，这样可以使选择排序的效率快一倍

例如

原始数组如下，使用选择排序进行排序，一趟选出最小和最大元素进行交换

变量left和变量right是数组的两端，mini和maxi分别代表最小和最大元素的下标

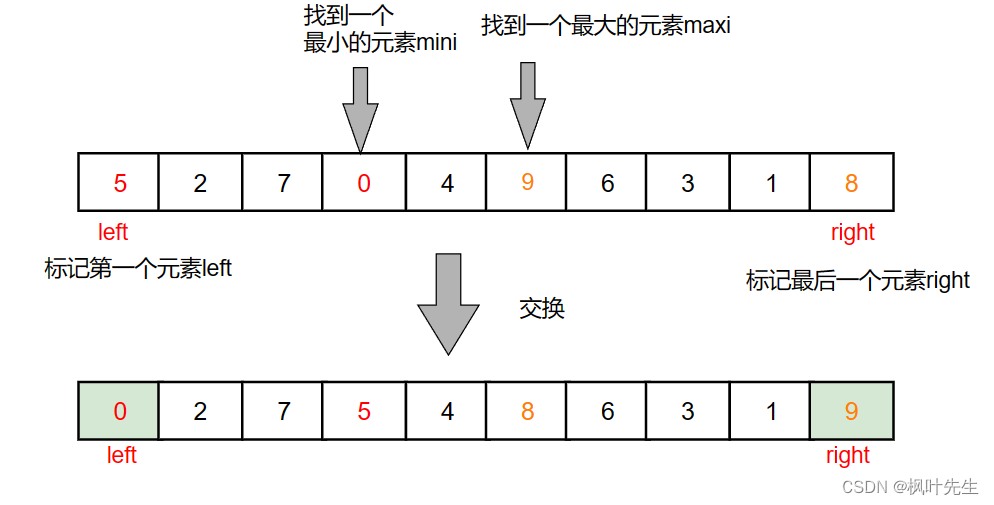
重复上述动作，直到数组有序

优化后的问题

如果maxi的位置与left重合，则left先与mini的位置交换，此时maxi位置的最大值被交换走，导致riight与maxi交换的数值是错误的（图中的0是10，打少了一个1）

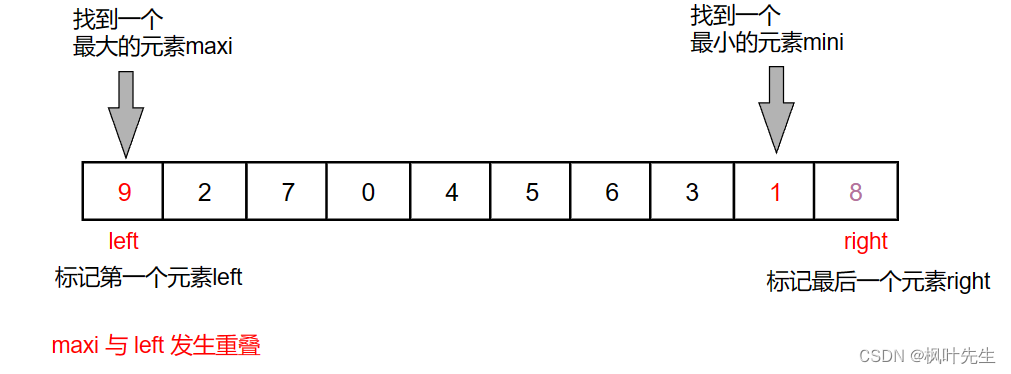
left先与mini的位置交换数据，此时maxi位置的已经不是最大值了（图中的0是10，打少了一个1）

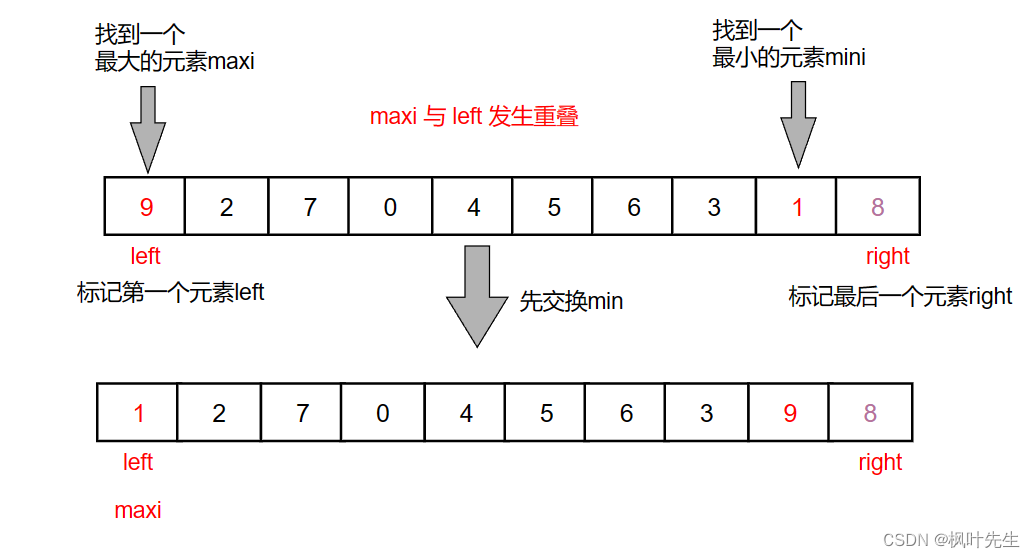
接着maxi再与right位置交换数据，排序就发生了错误

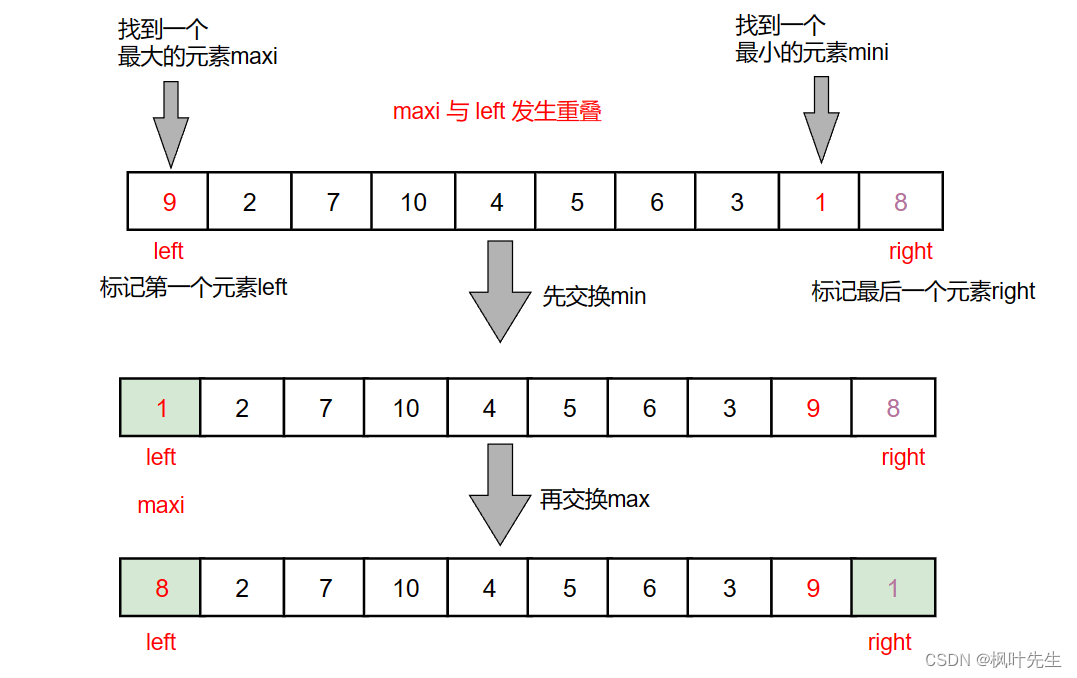
解决

​当maxi与left重合时，left与mini交换后导致maxi指向的不再是最大值，所以当我们对left交换后，就要对maxi进行一个修正，让maxi指向最大值，然后完成right的交换，如下：

当maxi与left重合，并且left此时完成了交换，此时最大值已经交换到了mini所指向的位置

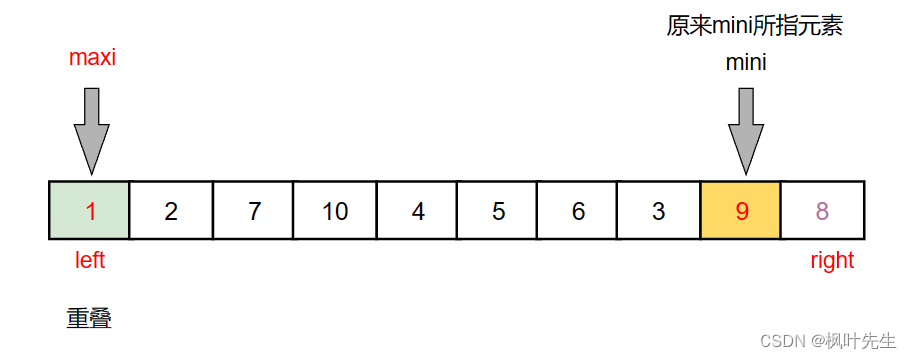
然后对maxi进行修正后，maxi = mini，再完成与right的交换

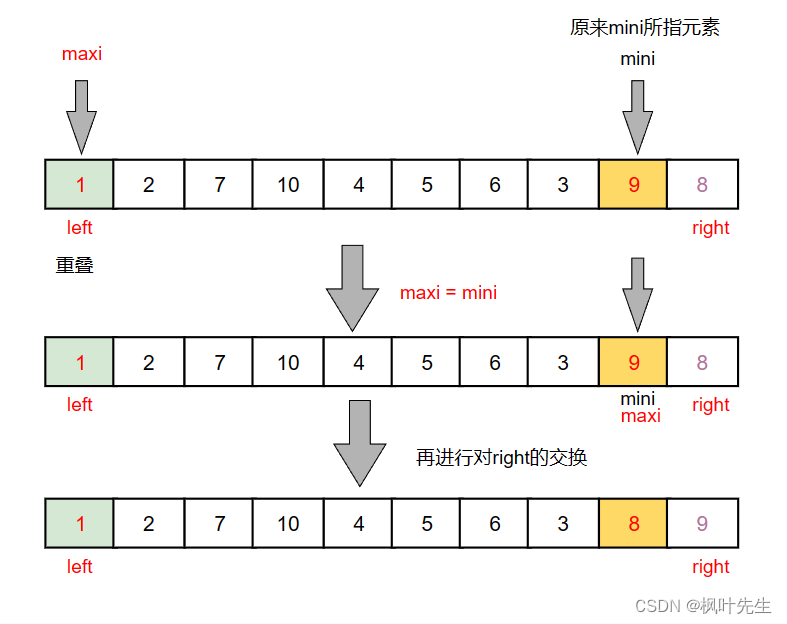
此时便解决了该问题

C++代码如下：

// 选择排序（选两个: 最小和最大）
void SelectSort(vector<int>& arr)
{
	int n = arr.size();
	int left = 0, right = n - 1; // 保存单趟排序的第一个数和最后一个数下标
	while (left < right)
	{
		int mini = left, maxi = left; // 保存最小值和最大值的下标
		// 选出最小值和最大值的下标
		for (int i = left + 1; i <= right; i++)
		{
			if (arr[mini] > arr[i]) mini = i;

			if (arr[i] > arr[maxi]) maxi = i;
		}
		// 最小值放在 arr[left]
		swap(arr[left], arr[mini]);
		// left 和 maxi 重叠的时候， 上一步已经把最大值换到 arr[mini] 中去了， 修正一下最大值 maxi 位置即可
		if (left == maxi) maxi = mini;
		// 最大值放在 arr[end] 
		swap(arr[right], arr[maxi]);
		left++;
		right--;
	}
}

1.3 特性总结

选择排序特性总结

• 选择排序思考非常好理解，但是效率不是很好，实际中很少使用
• 时间复杂度：O(N^2)
• 空间复杂度：O(1)
• 稳定性：不稳定
• 适用范围：选择排序适用于小规模数据的排序，对于大规模数据效率较低

--------------------- END ----------------------

「 作者 」 枫叶先生
「 更新 」 2024.1.11
「 声明 」 余之才疏学浅，故所撰文疏漏难免，
          或有谬误或不准确之处，敬请读者批评指正。