原理

最大公约数

有两个数字n和m。现在要求两个数字的最大公约数。
例如：n为18，m为4.
正常我们的思路求解最大公约数是暴力破解，遍历一遍公约数，取最大的那个，但是这样有一个问题，就是时间复杂度过高了。
有没有什么优化的方法呢？
我们可以先把18变成18-4=14，然后求和4的最大公约数；以此往复。但是每次都需要递减，碰到1000001和200这样的数字时，时间复杂度还是很高。
所以我们需要有最优化的方法
我们可以把数字递减理解为除以数字很多次，那么就变成了18对4取余，此时变为2和4；然后我们把4对2取余，此时变为2和0；那么最终结果就为2.

最小公倍数

通过观察18和4两个数字，发现18 = 2 * 9； 4 = 2 * 2；9和2都是质数，而2则是共同的最大公约数。
我们假设有两个数字n和m。

n = k * a  -- 1式
m = k * b  -- 2式
那么gcd（n，m）=k.

所以我们把1式和2式相乘，左边=n * m，右边=k * k * a * b。
就得到n * m = gcd（n， m） * k * a * b
此时的a * b * k 正好式n和m的最小公倍数，所以就得到

n * m = gcd（n， m） *  lcm（n， m）

代码

#include <iostream>

using namespace std;

//定义gcd求最大公约数的函数
int gcd(int num1, int num2) {
	if (num1 == num2) {
		return num1;
	}
	else if (num1 < num2) {
		return 	num1 == 0 ? num2 : gcd(num1, num2 % num1);
	}
	else {
		return gcd(num2, num1);
	}
}

// 定义最小公倍数的函数
int lcm(int num1, int num2) {
	return num1 / gcd(num1, num2) * num2;
}

int main() {
	int n, m;
	cout << "输入两个数字n和m：\n";
	cin >> n >> m;
	printf("%d和%d的最大公约数为%d \n", n, m, gcd(n, m));
	printf("%d和%d的最小公倍数为%d", n, m, lcm(n, m));
	return 0;
}

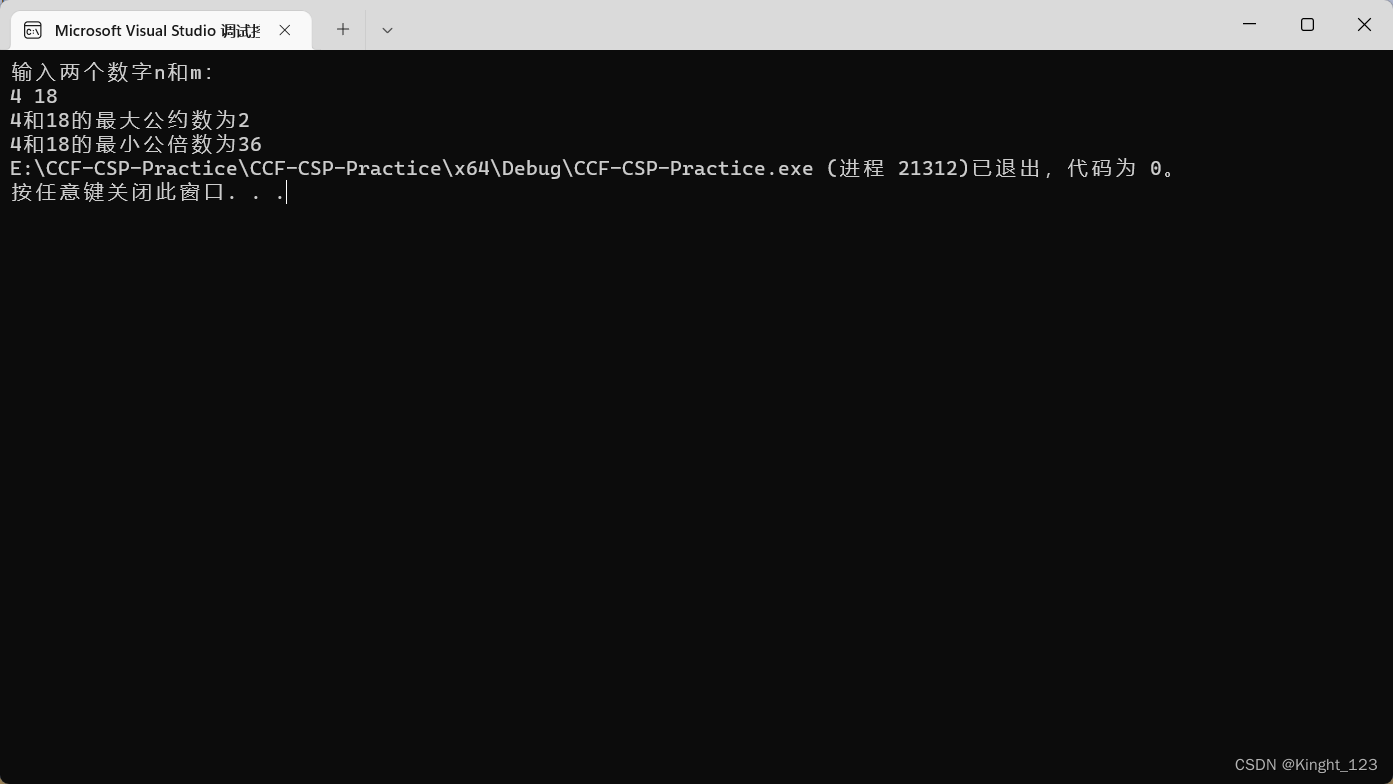
运行结果