1.题目

机器人正在玩一个古老的基于 DOS 的游戏。

游戏中有 N+1 座建筑——从 0 到 N 编号，从左到右排列。

编号为 0 的建筑高度为 0 个单位，编号为 i 的建筑高度为 H(i) 个单位。

起初，机器人在编号为 0 的建筑处。

每一步，它跳到下一个（右边）建筑。

假设机器人在第 k 个建筑，且它现在的能量值是 E，下一步它将跳到第 k+1 个建筑。

如果 H(k+1)>E，那么机器人就失去 H(k+1)−E 的能量值，否则它将得到 E−H(k+1) 的能量值。

游戏目标是到达第 N 个建筑，在这个过程中能量值不能为负数个单位。

现在的问题是机器人至少以多少能量值开始游戏，才可以保证成功完成游戏？

2.基本思想

二分

H (k+1) >E 即 E -（ H(k+1) − E ）
H (k+1)<=E 即 E +（ E − H(k+1) ）

化简 两种情况即 2E - H(k+1) ）

对于

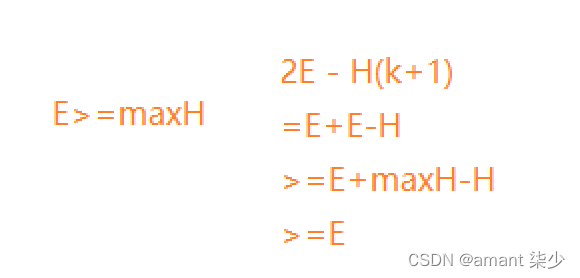
3.代码实现

import java.io.*;

public class _730机器人问题 {
    static int N = 100010;
    static int n;
    static int h[] = new int[N];

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        n=Integer.parseInt(br.readLine());
        String s[] =br.readLine().split(" ");
        for (int i = 1; i <= n; i++)
            h[i] =Integer.parseInt(s[i-1]);

        //二分
        int l = 0, r = N;
        while (l < r) {
            int mid = l + r >> 1;
            if (check(mid)) r = mid;
            else l = mid + 1;
        }
        System.out.println(l);
    }

    //校验 传入能量为mid是否符合
    private static boolean check(int e) {
        //遍历每个建筑 是否符合 任意时刻 e>0 、 2*e-h > 0
        for (int i = 1; i <= n; i++) {
            e = 2 * e - h[i];
            if (e >= N) return true;
            if (e < 0) return false;
        }
        return true;
    }
}