Description

小J占山为王有一段时间了，他决定把自己的地盘打扮一下---将各种颜色的旗插在山头上

当然某一座的山头只能用一种颜色的旗。

整个地盘有N个山头，可看成是一棵有N个节点的树。

小J还是有一点艺术细胞的，他不想整个地盘杂乱无章。

于是他规定手下，如果某两座山之间的距离<=2的话，则这两座山不能用同一种颜色的旗

小J一共采购了ｘ种颜色的旗。

请输出方案数，由于答案可能过大，请将其对10^9+7取模。

Format

Input

第一行一个数n,k，含义如题

接下来共有n-1行，两个数u,v表示u和v之间存在一条边

1≤n,x≤1e5,

Output

如题

Samples

输入数据 1

4 3

1 2

2 3

3 4

输出数据 1

6

---

先定下根的方案数(k种)

dfs递归下去

对于u的第一个子结点v，如果v没有爷爷点，就有k - 1种，如果有就k - 2种。

对于v的兄弟点，则每个点均比它左边的点的方案数少1(因为v的兄弟点根v的距离<=2)

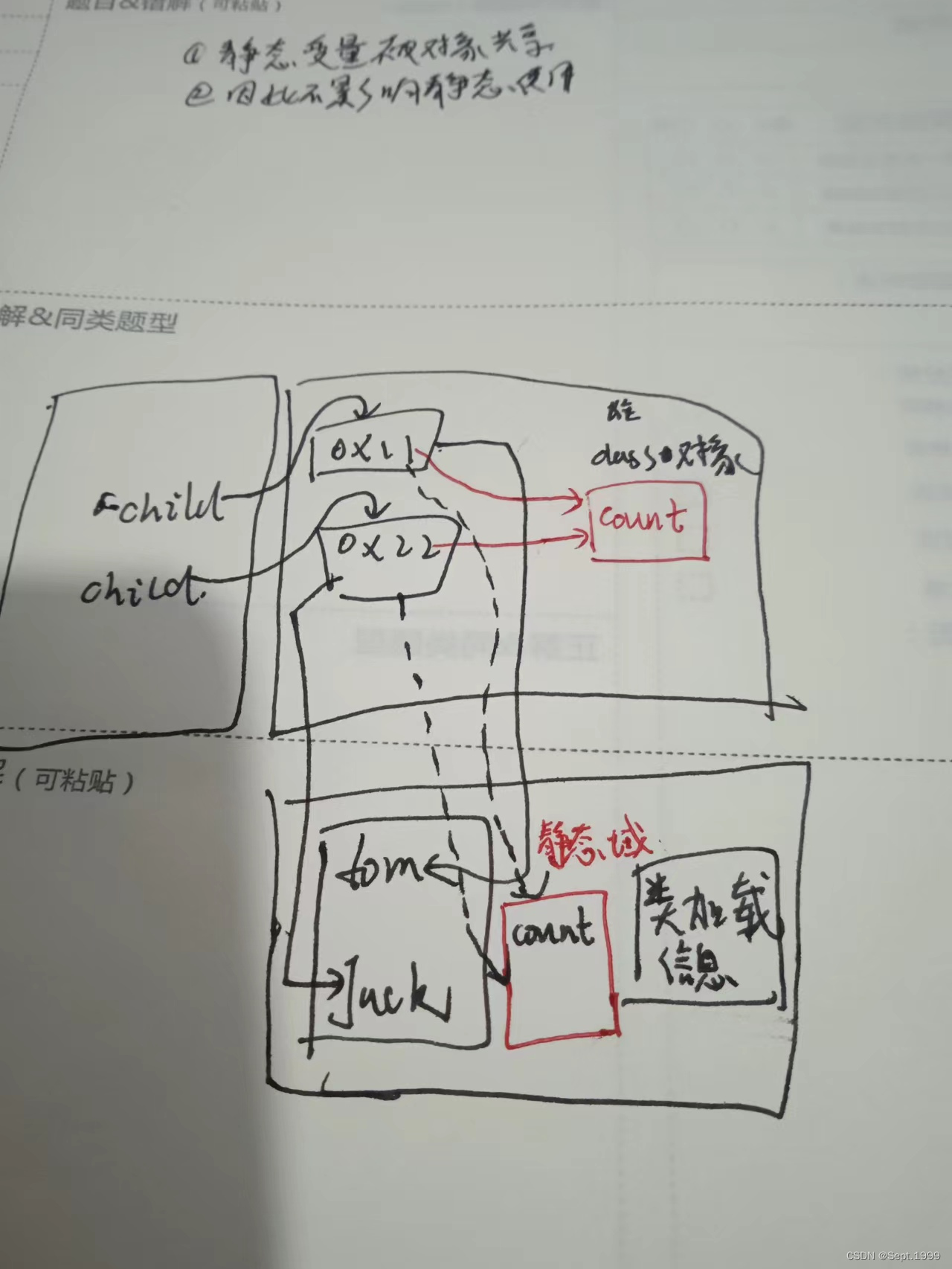
比如:

那么最后答案就是那些节点的方案数之积。注意:如果一个节点的方案数为负数,就直接输出0即可。

#include <bits/stdc++.h>
using namespace std;
#define int long long
int n,k,u,v,a[200001],eg,h[200001],vtx[200001],nxt[200001],ans = 1,deep[200001],mod = 1e9 + 7;
void adeg(int u,int v)
{
  eg++;
  nxt[eg] = h[u];
  h[u] = eg;
  vtx[eg] = v;
}
void dfs_2(int u,int fa,int gra)
{
  bool fl = 1;
  int p;
  for(int i = h[u]; i; i = nxt[i])
  {
    int v = vtx[i];
    if(v == fa) continue;
    if(fl == 1)//此时i是u的第一个子节点
    {
        fl = 0;
        if(gra == 0) a[v] = k - 1;
        else a[v] = k - 2;
        p = a[v];
    }
    else a[v] = --p;
    dfs_2(v,u,fa + 1);
  }
}
signed main()
{
  cin>>n>>k;
  for(int i = 1; i < n; i++)
  {
    cin>>u>>v;
    adeg(u,v);
    adeg(v,u);
  }
  a[1] = k;
  dfs_2(1,0,0);
  for(int i = 1; i <= n; i++)
  {
    ans *= a[i];
    ans %= mod;
    if(a[i] < 0)
    {
      cout<<0;
      return 0;
    }
  }
  cout<<ans;
  return 0;
}