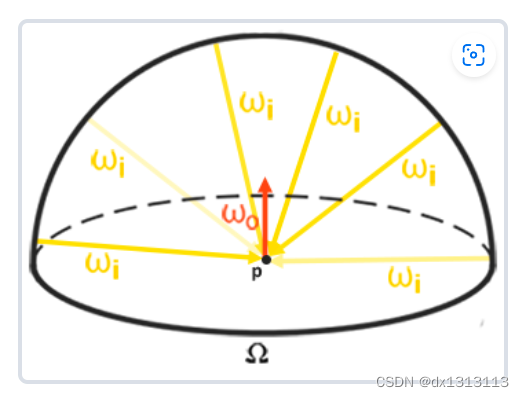
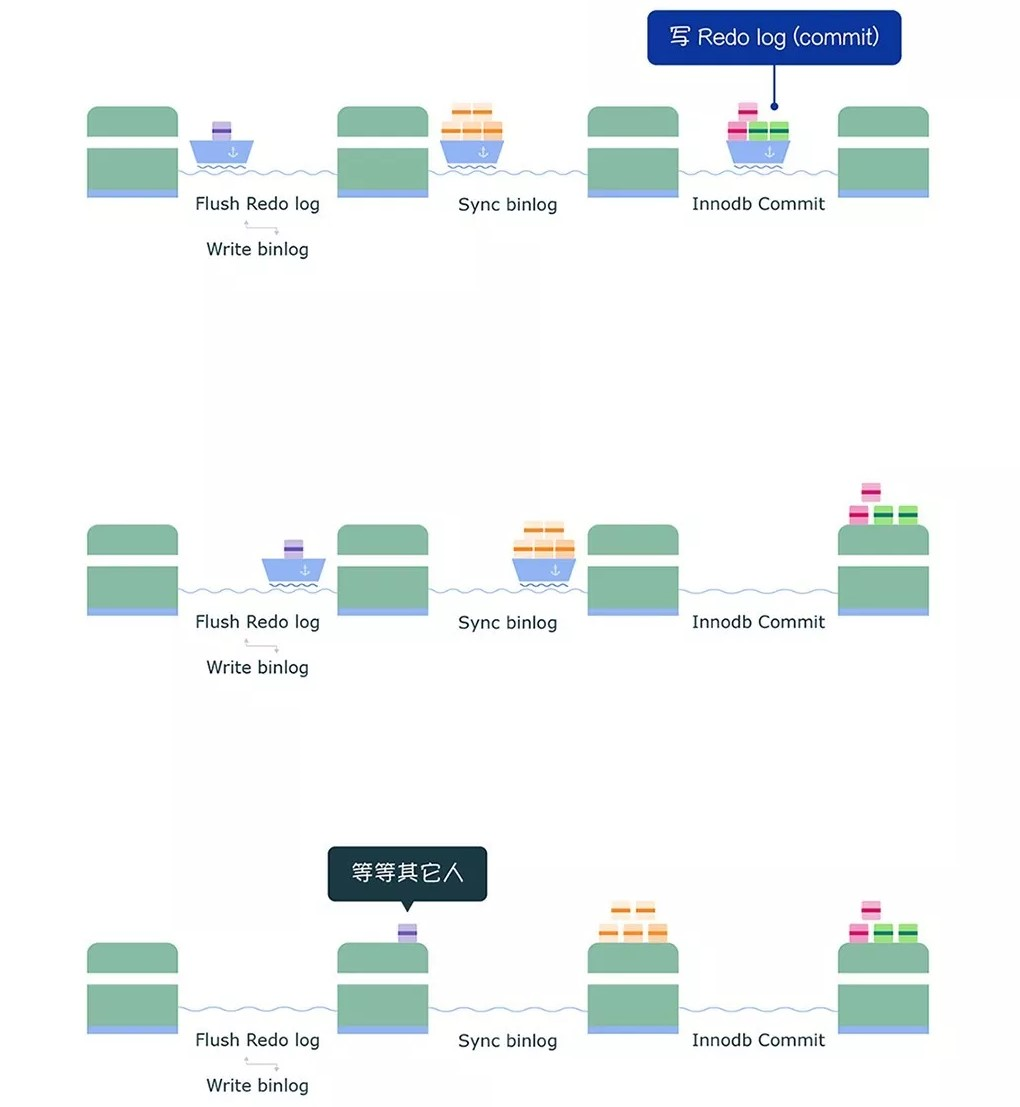
反射方程的分解、预计算BRDF

反射方程

仔细研究反射方程可以发现BRDF的漫反射kd和镜面反射ks是相互独立的，所以可以将方程分解为两部分：

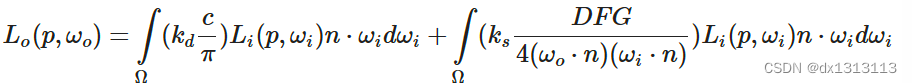
通过分别积分两部分再求即可得到最终的反射结果。

漫反射部分

仔细观察漫反射积分，我们发现漫反射兰伯特项是一个常数项（颜色 c 、折射率 kd 和 π 在整个积分是常数），不依赖于任何积分变量。基于此，我们可以将常数项移出漫反射积分：

这给了我们一个只依赖于 wi的积分（假设 p 位于环境贴图的中心）。有了这些知识，我们就可以计算或预计算一个新的立方体贴图，它在每个采样方向——也就是纹素——中存储漫反射积分的结果，这些结果是通过卷积计算出来的。

卷积的特性是，对数据集中的一个条目做一些计算时，要考虑到数据集中的所有其他条目。这里的数据集就是场景的辐射度或环境贴图。因此，要对立方体贴图中的每个采样方向做计算，我们都会考虑半球 Ω 上的所有其他采样方向。

为了对环境贴图进行卷积，我们通过对半球 Ω上的大量方向进行离散采样并对其辐射度取平均值，来计算每个输出采样方向 wo的积分。用来采样方向 wi的半球，要面向卷积的输出采样方向 wo。

这个预计算的立方体贴图，在每个采样方向 wo上存储其积分结果，可以理解为场景中所有能够击中面向 wo 的表面的间接漫反射光的预计算总和。这样的立方体贴图被称为辐照度图，因为经过卷积计算的立方体贴图能让我们从任何方向有效地直接采样场景（预计算好的）辐照度。

下面是一个环境立方体贴图及其生成的辐照度图的示例（由 Wave 引擎提供），每个向wo 的场景辐射度取平均值。

由于立方体贴图每个纹素中存储了（ wo 方向的）卷积结果，辐照度图看起来有点像环境的平均颜色或光照图。使用任何一个向量对立方体贴图进行采样，就可以获取该方向上的场景辐照度。

然而，计算上又不可能从 Ω 的每个可能的方向采样环境光照，理论上可能的方向数量是无限的。不过我们可以对有限数量的方向采样以近似求解，在半球内均匀间隔或随机取方向可以获得一个相当精确的辐照度近似值，从而离散地计算积分 ∫。

然而，对于每个片段实时执行此操作仍然太昂贵，因为仍然需要非常大的样本数量才能获得不错的结果，因此我们希望可以预计算。既然半球的朝向决定了我们捕捉辐照度的位置，我们可以预先计算每个可能的半球朝向的辐照度，这些半球朝向涵盖了所有可能的出射方向 wo ：

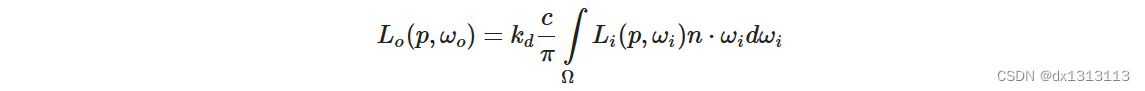
给定任何方向向量 wi ，我们可以对预计算的辐照度图采样以获取方向 wi的总漫反射辐照度。为了确定片段上间接漫反射光的数量（辐照度），我们获取以表面法线为中心的半球的总辐照度。获取场景辐照度的方法就简化为：

vec3 irradiance = texture(irradianceMap, N);

现在，为了生成辐照度贴图，我们需要将环境光照求卷积，转换为立方体贴图。假设对于每个片段，表面的半球朝向法向量 N ，对立方体贴图进行卷积等于计算朝向 N的半球 Ω中每个方向 wi的总平均辐射率。

镜面反射部分

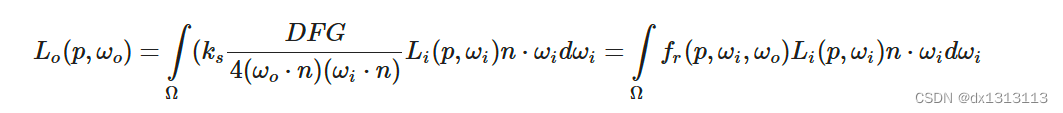
由于与辐射卷积相同的原因，无法以合理的性能实时地求解积分的镜面反射部分。所以最好可以预计算这个积分，以得到IBL贴图这样的东西，用片段的法线对这张图进行采样并计算。但是从这个积分中可以看出该积分与漫反射部分不同，它不仅仅依赖于wi 还依赖于 wo。所以无法使用两个方向向量采样预计算的立方体图。 Epic Games 的分割求和近似法将预计算分成两个单独的部分求解，再将两部分组合起来得到后文给出的预计算结果。分割求和近似法将镜面反射积分拆成两个独立的积分：

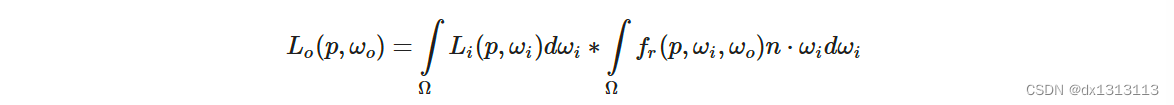
卷积的第一部分被称为预滤波环境贴图，它类似于辐照度图，是预先计算的环境卷积贴图，但这次考虑了粗糙度。因为随着粗糙度的增加，参与环境贴图卷积的采样向量会更分散，导致反射更模糊，所以对于卷积的每个粗糙度级别，我们将按顺序把模糊后的结果存储在预滤波贴图的 mipmap 中。例如，预过滤的环境贴图在其 5 个 mipmap 级别中存储 5 个不同粗糙度值的预卷积结果，如下图所示：

我们使用 Cook-Torrance BRDF 的法线分布函数(NDF)生成采样向量及其散射强度，该函数将法线和视角方向作为输入。由于我们在卷积环境贴图时事先不知道视角方向，因此 Epic Games 假设视角方向——也就是镜面反射方向——总是等于输出采样方向ωo，以作进一步近似。翻译成代码如下：

vec3 N = normalize(w_o);
vec3 R = N;
vec3 V = R;

这样，预过滤的环境卷积就不需要关心视角方向了。这意味着当从如下图的角度观察表面的镜面反射时，得到的掠角镜面反射效果不是很好（图片来自文章《Moving Frostbite to PBR》）。然而，通常可以认为这是一个体面的妥协：

等式的第二部分等于镜面反射积分的 BRDF 部分。如果我们假设每个方向的入射辐射度都是白色的（因此L(p,x)=1.0），就可以在给定粗糙度、光线 ωi法线 n夹角 n⋅ωi 的情况下，预计算 BRDF 的响应结果。Epic Games 将预计算好的 BRDF 对每个粗糙度和入射角的组合的响应结果存储在一张 2D 查找纹理(LUT)上，称为BRDF积分贴图。2D 查找纹理存储是菲涅耳响应的系数（R 通道）和偏差值（G 通道），它为我们提供了分割版镜面反射积分的第二个部分：

生成查找纹理的时候，我们以 BRDF 的输入n⋅ωi（范围在 0.0 和 1.0 之间）作为横坐标，以粗糙度作为纵坐标。有了此 BRDF 积分贴图和预过滤的环境贴图，我们就可以将两者结合起来，以获得镜面反射积分的结果：

float lod             = getMipLevelFromRoughness(roughness);
vec3 prefilteredColor = textureCubeLod(PrefilteredEnvMap, refVec, lod);
vec2 envBRDF          = texture2D(BRDFIntegrationMap, vec2(NdotV, roughness)).xy;
vec3 indirectSpecular = prefilteredColor * (F * envBRDF.x + envBRDF.y)

预计算BRDF（镜面部分）

回顾一下镜面部分的分割求和近似法：

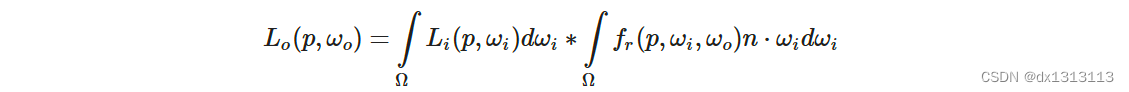
我们已经在预过滤贴图的各个粗糙度级别上预计算了分割求和近似的左半部分。右半部分要求我们在 n⋅ωo、表面粗糙度、菲涅尔系数 F0上计算 BRDF 方程的卷积。这等同于在纯白的环境光或者辐射度恒定为 Li=1.0 的设置下，对镜面 BRDF 求积分。对3个变量做卷积有点复杂，不过我们可以把 F0 移出镜面 BRDF 方程：

F为菲涅耳方程。将菲涅耳分母移到 BRDF 下面可以得到如下等式：

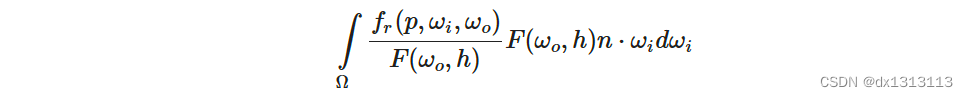
用 Fresnel-Schlick 近似公式替换右边的 F 可以得到：

让我们用 α 替换 $(1-\omega _{o}\cdot h)^{5}$ 以便更轻松地求解 F0：

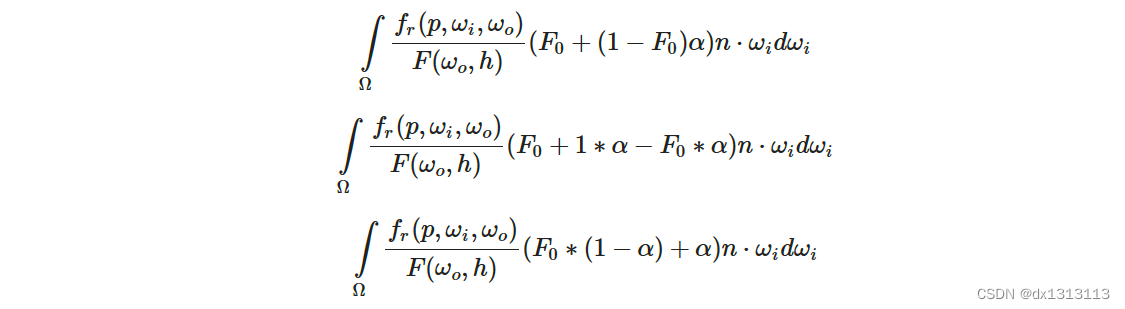
然后将菲涅耳函数 F分拆到两个积分里：

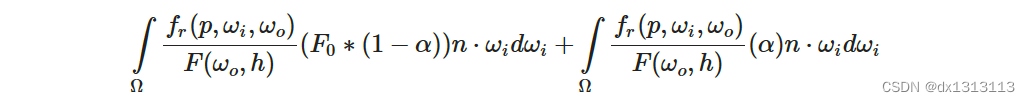
这样，F0在整个积分上是恒定的，我们可以从积分中提取出F0。接下来，我们将α替换回其原始形式，从而得到最终分割求和的 BRDF 方程：

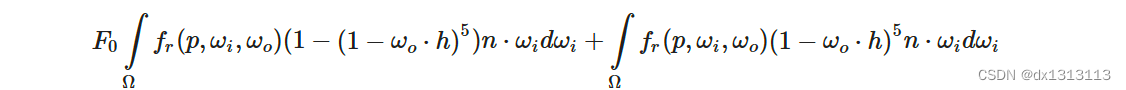
公式中的两个积分分别表示 F0 的比例和偏差。注意，由于 f(p,ωi,ωo)已经包含 F 项，它们被约分了，这里的 f 中不计算 F 项。

和之前卷积环境贴图类似，可以对 BRDF 方程求卷积，其输入是 n 和 ωo的夹角，以及粗糙度，并将卷积的结果存储在纹理中。我们将卷积后的结果存储在 2D 查找纹理（Look Up Texture, LUT）中，这张纹理被称为 BRDF 积分贴图，稍后会将其用于 PBR 光照着色器中，以获得间接镜面反射的最终卷积结果。

vec2 IntegrateBRDF(float NdotV, float roughness)
{
    vec3 V;
    V.x = sqrt(1.0 - NdotV*NdotV);
    V.y = 0.0;
    V.z = NdotV;

    float A = 0.0;
    float B = 0.0;

    vec3 N = vec3(0.0, 0.0, 1.0);

    const uint SAMPLE_COUNT = 1024u;
    for(uint i = 0u; i < SAMPLE_COUNT; ++i)
    {
        vec2 Xi = Hammersley(i, SAMPLE_COUNT);
        vec3 H  = ImportanceSampleGGX(Xi, N, roughness);
        vec3 L  = normalize(2.0 * dot(V, H) * H - V);

        float NdotL = max(L.z, 0.0);
        float NdotH = max(H.z, 0.0);
        float VdotH = max(dot(V, H), 0.0);

        if(NdotL > 0.0)
        {
            float G = GeometrySmith(N, V, L, roughness);
            float G_Vis = (G * VdotH) / (NdotH * NdotV);
            float Fc = pow(1.0 - VdotH, 5.0);

            A += (1.0 - Fc) * G_Vis;
            B += Fc * G_Vis;
        }
    }
    A /= float(SAMPLE_COUNT);
    B /= float(SAMPLE_COUNT);
    return vec2(A, B);
}
// ----------------------------------------------------------------------------
void main() 
{
    vec2 integratedBRDF = IntegrateBRDF(TexCoords.x, TexCoords.y);
    FragColor = integratedBRDF;
}

BRDF 卷积部分是从数学到代码的直接转换。我们将角度 θ 和粗糙度作为输入，以重要性采样产生采样向量，在整个几何体上结合 BRDF 的菲涅耳项对向量进行处理，然后输出每个样上 F0 的系数和偏差，最后取平均值。

细节：与 IBL 一起使用时，BRDF 的几何项略有不同，因为 k变量的含义稍有不同：

由于 BRDF 卷积是镜面 IBL 积分的一部分，因此我们要在 Schlick-GGX 几何函数中使用 $k_{IBL}$ ：

float GeometrySchlickGGX(float NdotV, float roughness)
{
    float a = roughness;
    float k = (a * a) / 2.0;

    float nom   = NdotV;
    float denom = NdotV * (1.0 - k) + k;

    return nom / denom;
}
// ----------------------------------------------------------------------------
float GeometrySmith(vec3 N, vec3 V, vec3 L, float roughness)
{
    float NdotV = max(dot(N, V), 0.0);
    float NdotL = max(dot(N, L), 0.0);
    float ggx2 = GeometrySchlickGGX(NdotV, roughness);
    float ggx1 = GeometrySchlickGGX(NdotL, roughness);

    return ggx1 * ggx2;
}

最后，为了存储 BRDF 卷积结果，需要生成一张 512 × 512 分辨率的 2D 纹理。

补充：

vec3 ImportanceSampleGGX(vec2 Xi, vec3 N, float roughness)
{
    float a = roughness*roughness;

    float phi = 2.0 * PI * Xi.x;
    float cosTheta = sqrt((1.0 - Xi.y) / (1.0 + (a*a - 1.0) * Xi.y));
    float sinTheta = sqrt(1.0 - cosTheta*cosTheta);

    // from spherical coordinates to cartesian coordinates
    vec3 H;
    H.x = cos(phi) * sinTheta;
    H.y = sin(phi) * sinTheta;
    H.z = cosTheta;

    // from tangent-space vector to world-space sample vector
    vec3 up        = abs(N.z) < 0.999 ? vec3(0.0, 0.0, 1.0) : vec3(1.0, 0.0, 0.0);
    vec3 tangent   = normalize(cross(up, N));
    vec3 bitangent = cross(N, tangent);

    vec3 sampleVec = tangent * H.x + bitangent * H.y + N * H.z;
    return normalize(sampleVec);
}

float RadicalInverse_VdC(uint bits) 
{
    bits = (bits << 16u) | (bits >> 16u);
    bits = ((bits & 0x55555555u) << 1u) | ((bits & 0xAAAAAAAAu) >> 1u);
    bits = ((bits & 0x33333333u) << 2u) | ((bits & 0xCCCCCCCCu) >> 2u);
    bits = ((bits & 0x0F0F0F0Fu) << 4u) | ((bits & 0xF0F0F0F0u) >> 4u);
    bits = ((bits & 0x00FF00FFu) << 8u) | ((bits & 0xFF00FF00u) >> 8u);
    return float(bits) * 2.3283064365386963e-10; // / 0x100000000
}
// ----------------------------------------------------------------------------
vec2 Hammersley(uint i, uint N)
{
    return vec2(float(i)/float(N), RadicalInverse_VdC(i));
}