Part.I Introduction

本文主要介绍了如何使用 Matlab 对数据的分布进行拟合。也就是 笔者对实现『用 Matlab 拟合出数据的概率分布密度函数』这个目标所进行的一些探索。

Part.II Distribution Fitter APP 的使用

Chap.I APP 简介

此 APP 界面如下所示：

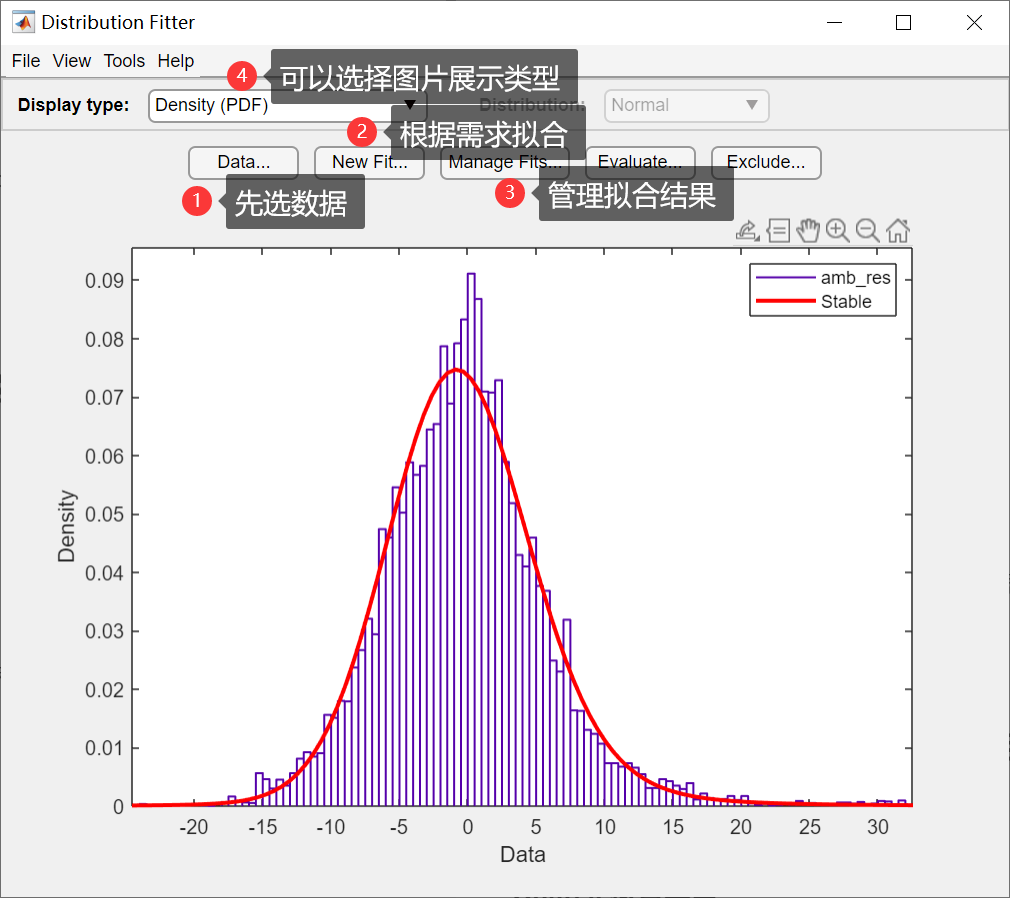
其中Display type 有如下几种：

• Density (PDF)：概率密度
• Cumulative probability CDF：累积概率分布
• Quantile (inverser CDF)：分位数 (逆 CDF)
• Probability plot：概率图
• Survivor funciton：剩余函数
• Cumulative hazard：累积危险函数

---

分布类型如下表所示

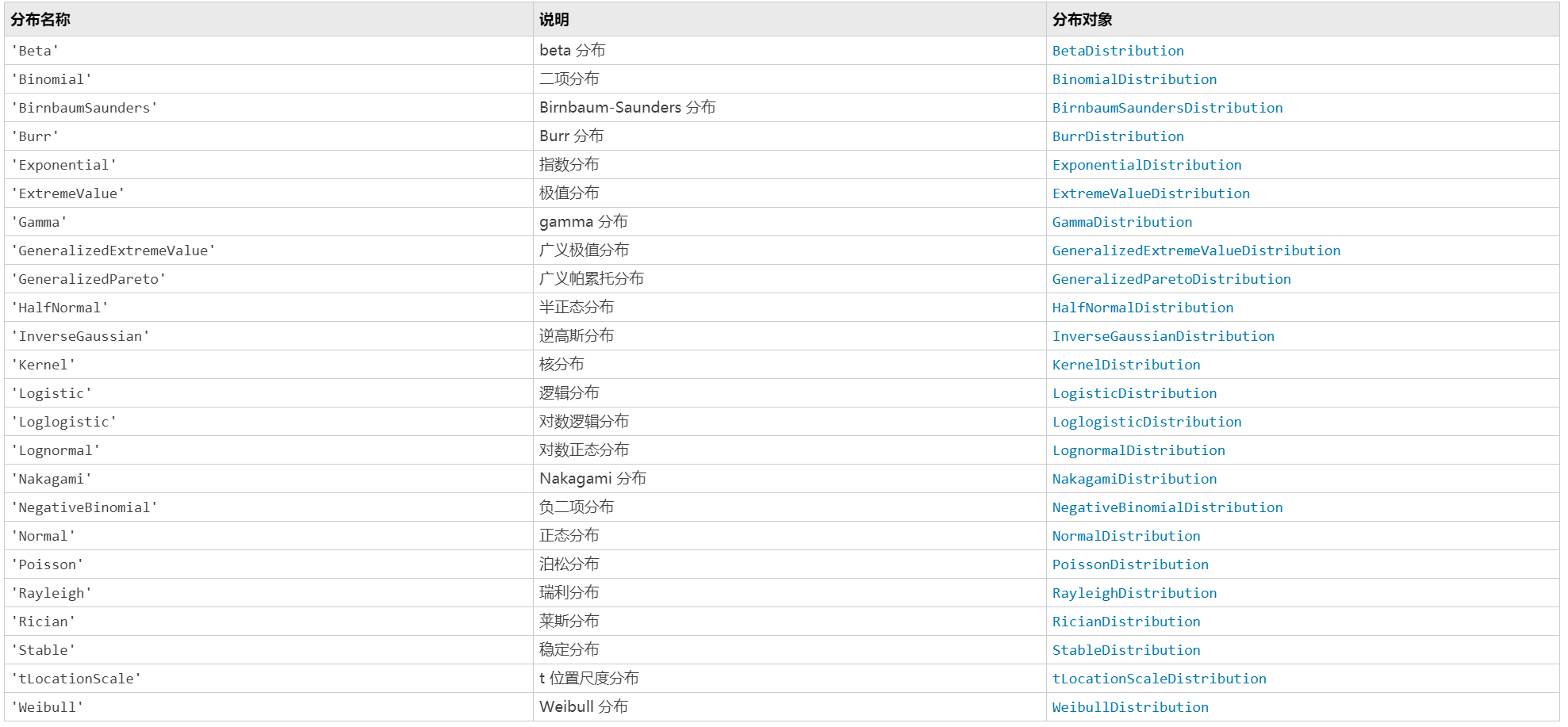
每种分布得到的拟合参数的个数和名字或将不同，这些可以参看 Matlab 的帮助文档。

---

Chap.II 简单使用

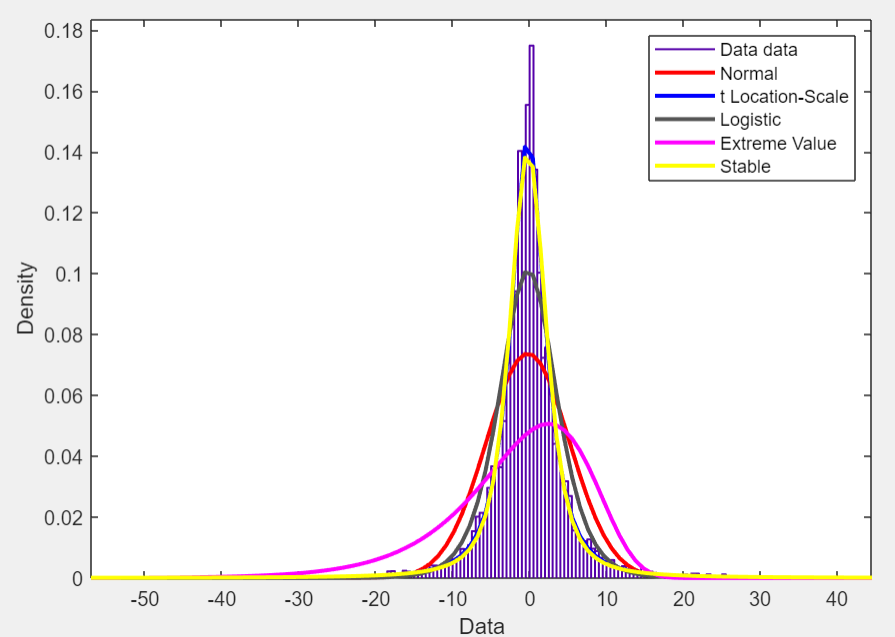
下面的一个图就是利用此 APP 生成的，上手很简单。

Part.III 通过代码实现分布拟合

Chap.I 基于 fitdist 函数

fitdist 函数或许就是 Distribution Fitter APP 底层实现的一个最为重要的核心函数。

首先介绍一下 fitdist 函数，它可以对数据进行概率分布对象拟合，常用的调用方法为：

pd = fitdist(x,distname)		// 一般用这个足矣
pd = fitdist(x,distname,Name,Value)
[pdca,gn,gl] = fitdist(x,distname,'By',groupvar)
[pdca,gn,gl] = fitdist(x,distname,'By',groupvar,Name,Value)

首先是输入参数：

• x：待进行分布拟合的数据
• distname：分布名称，参看上面『分布类型表』
• groupvar：分组变量，暂时用不到，之后可看说明文档

然后是输出参数：

• pd：概率分布，可用a = pd.a 来获取参数估值 a，一般用这个就行。
• pdca：概率分布对象
• gn：组标签
• gl：分组变量水平

---

下面是一个示例：

clc;clear
% 构造数据, 生成 10000 个服从 0~1 正态分布的数据
Data=randn(10000,1);
% 正态分布拟合
pd = fitdist(Data,'Normal');
a=pd.mu; b=pd.sigma;
% 绘图
pts=linspace(-5,5,1000);
[yy,xx]=ksdensity(Data,pts);
yy1=normpdf(xx,a,b);
% 绘制概率分布图
plot(xx,yy)
hold on
% 绘制拟合结果
plot(xx,yy1)
legend(['raw';'fit']);

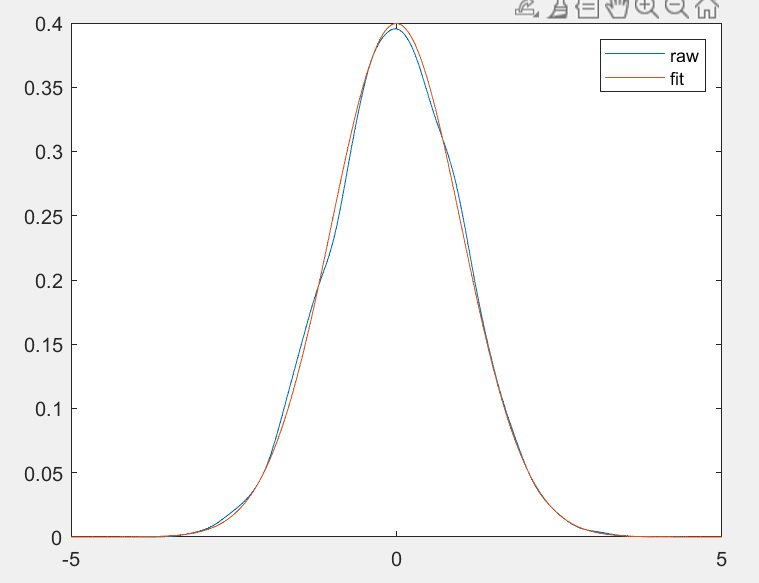
绘图结果如下：

Chap.II 获取数据的频率分布后进行曲线拟合

首先获取数据的频率分布（这一步比较关键）

// 获得的 xx1 和 yy1 只有100个点
[yy1,xx1]=ksdensity(Data);
// 通过 pts 来控制点的个数
pts = linspace(-20,20,1000);
// 根据 pts 获取数据的频率分布
[yy,xx]=ksdensity(Data,pts);

得到数据的概率分布之后，接下来实际上就是曲线拟合了！

---

下面是一个示例

clc;clear
% 构造数据, 生成 10000 个服从 N(0,5) 正态分布的数据
Data=normrnd(0,5,10000,1);
% 通过 pts 来控制点的个数
pts = linspace(-20,20,1000);
% 根据 pts 获取数据的频率分布
[yy,xx]=ksdensity(Data,pts);
% 定义拟合的公式
%fitEquation = fittype('1/(2*a)*exp(-abs(x-b)/a)', 'coefficients', {'a', 'b'});  % Laplace 分布
fitEquation = fittype('1/sqrt(2*pi)/b*exp(-(x-a)*(x-a)/(2*b*b))', 'coefficients', {'a', 'b'});
% 确定初值
initialGuess = [1, 6];
% 进行曲线拟合
fittedModel = fit(xx', yy', fitEquation, 'StartPoint', initialGuess);
% 展示拟合结果
disp(fittedModel);
% 绘图
plot(xx,yy)
hold on
a=fittedModel.a; b=fittedModel.b;
% yy1=1/(2*a)*exp(-abs(xx-b)/a);  % Laplace 分布
yy1=1/sqrt(2*pi)/b*exp(-(xx-a).*(xx-a)/(2*b*b));
plot(xx,yy1)
legend(['raw';'fit']);

得到的分布拟合结果为：

General model:
fittedModel(x) = 1/sqrt(2*pi)/b*exp(-(x-a)*(x-a)/(2*b*b))
Coefficients (with 95% confidence bounds):
    a =    0.008658  (-0.001162, 0.01848)
    b =       5.084  (5.076, 5.092)

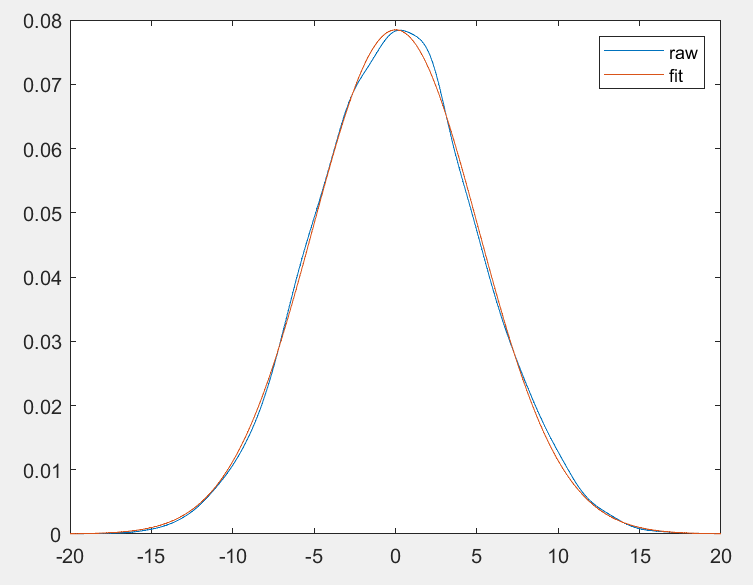
绘图结果为：

Reference

1. Matlab 之曲线拟合