Q-learning算法
主要思路
由于
V
π
(
s
)
=
∑
a
∈
A
π
(
a
∣
s
)
Q
π
(
s
,
a
)
V_\pi(s)=\sum_{a\in A}\pi(a\mid s)Q_\pi(s,a)
Vπ(s)=∑a∈Aπ(a∣s)Qπ(s,a) ,当我们直接预测动作价值函数,在决策中选择Q值最大即动作价值最大的动作,则可以使策略和动作价值函数同时最优,那么由上述公式可得,状态价值函数也是最优的。
Q
(
s
t
,
a
t
)
←
Q
(
s
t
,
a
t
)
+
α
[
r
t
+
γ
max
a
Q
(
s
t
+
1
,
a
)
−
Q
(
s
t
,
a
t
)
]
Q(s_t,a_t)\leftarrow Q(s_t,a_t)+\alpha[r_t+\gamma\max_aQ(s_{t+1},a)-Q(s_t,a_t)]
Q(st,at)←Q(st,at)+α[rt+γamaxQ(st+1,a)−Q(st,at)]
Q-learning基于时序差分的更新方法,具体流程如下所示:
- 初始化 Q ( s , a ) Q(s,a) Q(s,a)
- for 序列
e
=
1
→
E
e=1\to E
e=1→E do:
- 得到初始状态s
- for 时步
t
=
1
→
T
t=1\to T
t=1→T do:
- 使用 ϵ − g r e e d y \epsilon -greedy ϵ−greedy 策略根据Q选择当前状态s下的动作a
- 得到环境反馈 r , s ′ r,s' r,s′
- Q ( s , a ) ← Q ( s , a ) + α [ r + γ max a ′ Q ( s ′ , a ′ ) − Q ( s , a ) ] Q(s,a)\leftarrow Q(s,a)+\alpha[r+\gamma\max_{a^{\prime}}Q(s^{\prime},a^{\prime})-Q(s,a)] Q(s,a)←Q(s,a)+α[r+γmaxa′Q(s′,a′)−Q(s,a)]
- s ← s ′ s\gets s' s←s′
- end for
- end for
算法实战
我们在悬崖漫步环境下实习Q-learning算法。
首先创建悬崖漫步的环境:
import matplotlib.pyplot as plt
import numpy as np
from tqdm import tqdm # tqdm是显示循环进度条的库
class CliffWalkingEnv:
def __init__(self, ncol, nrow):
self.nrow = nrow
self.ncol = ncol
self.x = 0 # 记录当前智能体位置的横坐标
self.y = self.nrow - 1 # 记录当前智能体位置的纵坐标
def step(self, action): # 外部调用这个函数来改变当前位置
# 4种动作, change[0]:上, change[1]:下, change[2]:左, change[3]:右。坐标系原点(0,0)
# 定义在左上角
change = [[0, -1], [0, 1], [-1, 0], [1, 0]]
self.x = min(self.ncol - 1, max(0, self.x + change[action][0]))
self.y = min(self.nrow - 1, max(0, self.y + change[action][1]))
next_state = self.y * self.ncol + self.x
reward = -1
done = False
if self.y == self.nrow - 1 and self.x > 0: # 下一个位置在悬崖或者目标
done = True
if self.x != self.ncol - 1:
reward = -100
return next_state, reward, done
def reset(self): # 回归初始状态,坐标轴原点在左上角
self.x = 0
self.y = self.nrow - 1
return self.y * self.ncol + self.x
创建Q-learning算法
class QLearning:
def __init__(self, ncol, nrow, epsilon, alpha, gamma,n_action=4):
self.epsilon = epsilon # 随机探索的概率
self.alpha = alpha # 学习率
self.gamma = gamma # 折扣因子
self.n_action = n_action # 动作数量
# 给每一个状态创建一个长度为4的列表。
self.Q_table = np.zeros([nrow*ncol,n_action]) # 初始化Q(s,a)
def take_action(self,state):
# 选取下一步的操作
if np.random.random()<self.epsilon:
action = np.random.randint(self.n_action) # 随机探索
else:
action = np.argmax(self.Q_table[state]) # 贪婪策略,选择Q值最大的动作
return action
def best_action(self, state): # 用于打印策略
Q_max = np.max(self.Q_table[state])
a = [0 for _ in range(self.n_action)]
for i in range(self.n_action):
if self.Q_table[state, i] == Q_max:
a[i] = 1
return a
def update(self,s0,a0,r,s1):
td_error = r+self.gamma*self.Q_table[s1].max()-self.Q_table[s0,a0]
self.Q_table[s0, a0] += self.alpha * td_error
ncol = 12
nrow = 4
np.random.seed(0)
epsilon = 0.1
alpha = 0.1
gamma = 0.9
env = CliffWalkingEnv(ncol, nrow)
agent = QLearning(ncol, nrow, epsilon, alpha, gamma)
num_episodes = 500 # 智能体在环境中运行的序列的数量
return_list = [] # 记录每一条序列的回报
# 显示10个进度条
for i in range(10):
# tqdm的进度条功能
with tqdm(total=int(num_episodes / 10), desc='Iteration %d' % i) as pbar:
for i_episode in range(int(num_episodes / 10)): # 每个进度条的序列数
episode_return = 0
state = env.reset()
done = False
while not done:
action = agent.take_action(state)
next_state, reward, done = env.step(action)
episode_return += reward # 这里回报的计算不进行折扣因子衰减
agent.update(state, action, reward, next_state)
state = next_state
return_list.append(episode_return)
if (i_episode + 1) % 10 == 0: # 每10条序列打印一下这10条序列的平均回报
pbar.set_postfix({
'episode':
'%d' % (num_episodes / 10 * i + i_episode + 1),
'return':
'%.3f' % np.mean(return_list[-10:])
})
pbar.update(1)
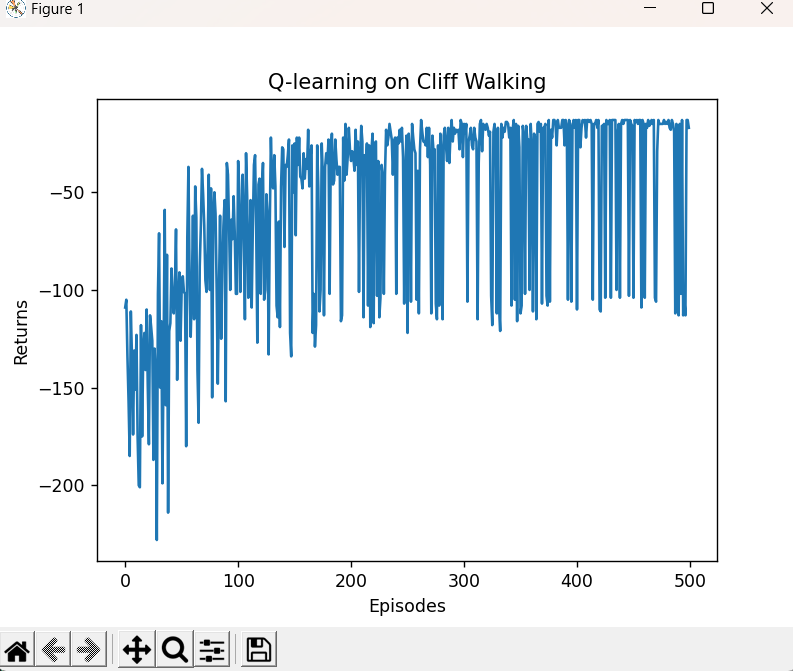
episodes_list = list(range(len(return_list)))
plt.plot(episodes_list, return_list)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('Q-learning on {}'.format('Cliff Walking'))
plt.show()
action_meaning = ['^', 'v', '<', '>']
print('Q-learning算法最终收敛得到的策略为:')
def print_agent(agent, env, action_meaning, disaster=[], end=[]):
for i in range(env.nrow):
for j in range(env.ncol):
if (i * env.ncol + j) in disaster:
print('****', end=' ')
elif (i * env.ncol + j) in end:
print('EEEE', end=' ')
else:
a = agent.best_action(i * env.ncol + j)
pi_str = ''
for k in range(len(action_meaning)):
pi_str += action_meaning[k] if a[k] > 0 else 'o'
print(pi_str, end=' ')
print()
action_meaning = ['^', 'v', '<', '>']
print('Sarsa算法最终收敛得到的策略为:')
print_agent(agent, env, action_meaning, list(range(37, 47)), [47])
print_agent(agent, env, action_meaning, list(range(37, 47)), [47])
Iteration 0: 100%|███████████████████████████████████████████████████████████████████| 50/50 [00:00<00:00, 2040.03it/s, episode=50, return=-105.700]
Iteration 1: 100%|███████████████████████████████████████████████████████████████████| 50/50 [00:00<00:00, 2381.99it/s, episode=100, return=-70.900]
Iteration 2: 100%|███████████████████████████████████████████████████████████████████| 50/50 [00:00<00:00, 3209.35it/s, episode=150, return=-56.500]
Iteration 3: 100%|███████████████████████████████████████████████████████████████████| 50/50 [00:00<00:00, 3541.95it/s, episode=200, return=-46.500]
Iteration 4: 100%|███████████████████████████████████████████████████████████████████| 50/50 [00:00<00:00, 5005.26it/s, episode=250, return=-40.800]
Iteration 5: 100%|███████████████████████████████████████████████████████████████████| 50/50 [00:00<00:00, 3936.76it/s, episode=300, return=-20.400]
Iteration 6: 100%|███████████████████████████████████████████████████████████████████| 50/50 [00:00<00:00, 4892.00it/s, episode=350, return=-45.700]
Iteration 7: 100%|███████████████████████████████████████████████████████████████████| 50/50 [00:00<00:00, 5502.60it/s, episode=400, return=-32.800]
Iteration 8: 100%|███████████████████████████████████████████████████████████████████| 50/50 [00:00<00:00, 6730.49it/s, episode=450, return=-22.700]
Iteration 9: 100%|███████████████████████████████████████████████████████████████████| 50/50 [00:00<00:00, 6768.50it/s, episode=500, return=-61.700]
Q-learning算法最终收敛得到的策略为:
Qling算法最终收敛得到的策略为:
^ooo ovoo ovoo ^ooo ^ooo ovoo ooo> ^ooo ^ooo ooo> ooo> ovoo
ooo> ooo> ooo> ooo> ooo> ooo> ^ooo ooo> ooo> ooo> ooo> ovoo
ooo> ooo> ooo> ooo> ooo> ooo> ooo> ooo> ooo> ooo> ooo> ovoo
^ooo **** **** **** **** **** **** **** **** **** **** EEEE
^ooo ovoo ovoo ^ooo ^ooo ovoo ooo> ^ooo ^ooo ooo> ooo> ovoo
ooo> ooo> ooo> ooo> ooo> ooo> ^ooo ooo> ooo> ooo> ooo> ovoo
ooo> ooo> ooo> ooo> ooo> ooo> ooo> ooo> ooo> ooo> ooo> ovoo
^ooo **** **** **** **** **** **** **** **** **** **** EEEE




![【算法每日一练]-动态规划 (保姆级教程 篇15) #纸带 #围栏木桩 #四柱河内塔](https://img-blog.csdnimg.cn/direct/1cea3486216242abb2b62aff231340d4.png)







![[机缘参悟-122] :IT人如何认识自己的?自省、面试、考核、咨询?](https://img-blog.csdnimg.cn/direct/e9d6f01a396a485e83648700c9bf201e.png)