增广路算法 DFS求解最大网络流问题

news2024/11/18 23:44:59

最大网络流问题

最大网络流问题是这样的，有一个有向图，假定有一个源点，有一个汇点，源点有流量出来，汇点有流量进入，有向图上的边的权重为该条边可通过的最大流量(方向为边的方向)，问从源点到汇点这条路径上，可以通过的流量总和最大是多少？注意并不一定是只有一条路径，多条路径加起来只要不冲突也行。

DFS求解增广路算法

首先作几点额外的说明：

1.可以认为A[i][j]表示从i到j的可行流，A[j][i]表示从j到i的可行流，A[i][j]+A[j][i]始终是保持不变的
2.初始时若A[i][j]非零则A[j][i]必然为0，若A[i][j]为INF则A[j][i]必然也为INF,对角线上必然都是INF
3.下面步骤中描述的左值为与图中箭头方向相同的可行流，右值为与图中方向相反的可行流
(默认源点只出不进、汇点只进不出)

思路

增广路算法的步骤
step1：设置visit访问标记数组，flag标记用于检查此次dfs是否寻找到final，set集合用于存放当前路径上的点
step2：循环step3
step3：从源点开始dfs，如果flag=0则继续下面步骤。

如果发现进入到汇点则置flag=1，并将此次dfs路径上的左值减去min，右值加上min；
如果没有进入final则继续进行dfs，对符合条件的顶点标记访问并将其加入set集合

step4：统计m[i][start]或m[final][i]的和，也就是源点此时出去的流量总和或者汇点流量进入的总和，此结果即为最大网络流问题的解

代码

#include"iostream"
using namespace std;
#define Maxn 100
#define INF 1e9

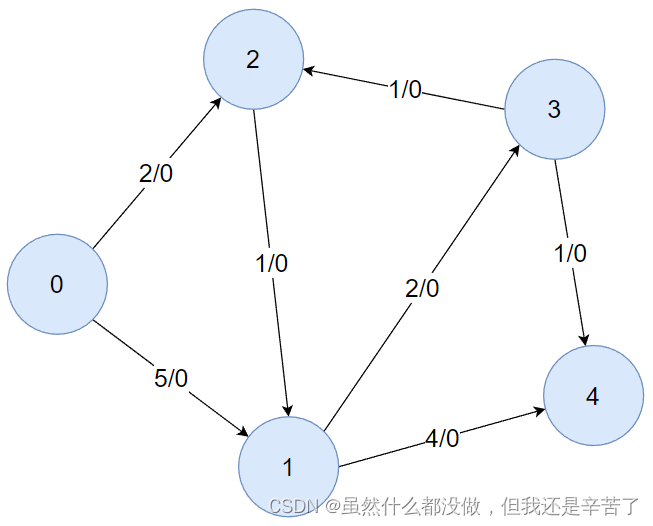
int m[Maxn][Maxn]=// 对应下图 
{
{INF,5,2,INF,INF},
{0,INF,0,2,4},
{0,1,INF,0,INF},
{INF,0,1,INF,1},
{INF,0,INF,0,INF} 
};
int n=5,start=0,final=4,Min,len,set[Maxn],visit[Maxn]; 
int flag;
void FF(int v)
{
	if(flag==1)// 每次只进行一次dfs 
		return ;
	if(v==final)// 找到汇点 标记置1 并对沿途路径上的边权值做更改
	{
		flag=1;
		for(int i=0;i<len-1;i++)
		{
			m[set[i]][set[i+1]]-=Min;
			m[set[i+1]][set[i]]+=Min;
		}
	}
	for(int i=0;i<n;i++)
	{
		if(m[v][i]!=0&&m[v][i]!=INF&&visit[i]==0)
		{
			if(m[v][i]<Min)
				Min=m[v][i];
			visit[i]=1;
			set[len++]=i;
			FF(i);
			len--;
			visit[i]=0;
		}
	}
}
// 统计源点出去的流量
void Print()
{
	int res=0;
	for(int i=0;i<n;i++)
	{
		if(m[i][start]!=INF)
			res+=m[i][start];
	}
	cout<<"result:"<<res<<endl;
}
int main()
{
	while(1)
	{
		Min=INF; // 这里不要忘了 
		for(int i=0;i<n;i++)
			visit[i]=0;
		visit[start]=1; // 这里不要忘了 
		set[len++]=start;
		FF(start);
		if(flag==0)
			break;
		flag=0;
	}
	Print();
	return 0;
}