目录
1.线性规划的基本公式
例题: 编辑编辑
1.符号
2.基本假设
3.模型的分析与建立
那么可以得出目标函数是
约束条件是
一.固定风险水平,优化收益
二.固定盈利水平,极小化风险
三.设置一个投资偏好系数S
语法解析
代码
输出结果
结论
1.线性规划的基本公式

[x,fval]=linProg(c,A,b,Aeq,Beq,lb,ub)
例题: 
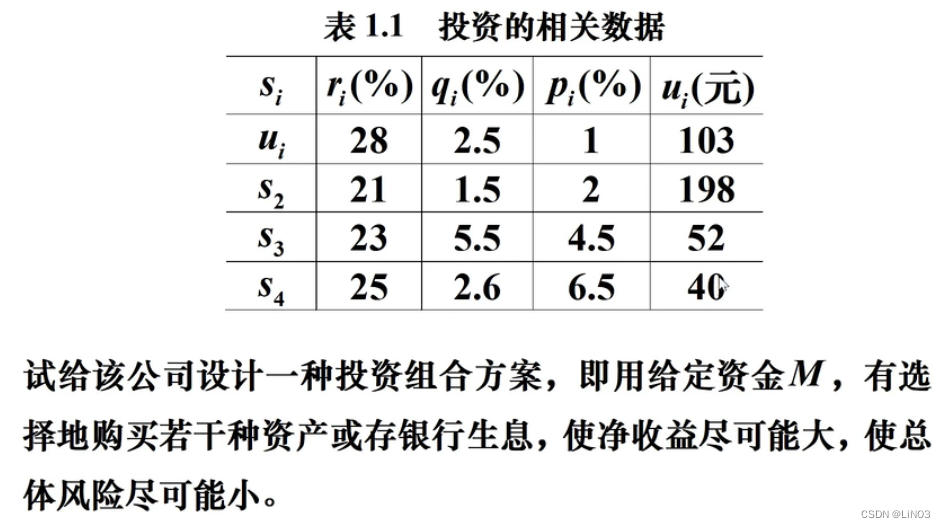
1.符号
a代表投资风险度
Q代表总体收益
其余的如题
2.基本假设
- 投资数额M非常大,为方便计算,假设M=1;(所有的投资数加上所有的交易费等于投资额)
- 投资越分散,总的风险越小
- 总体风险用投资项目中最大的一个风险来度量
- n+1种资产(n个项目加存银行)之间相互独立
- 投资期间r,p,q都是定值,不受意外因素影响
- 净收益和总体风险只受r,p,q影响,不受其他因素干扰
3.模型的分析与建立
1.因为总体风险用投资项目中最大的一个风险来度量
所以风险就是所有qi*xi中最大的一个。
max{qi*xi|i=1,2,L,n}
2.购买所支付的交易额是个分段函数
但是题目给定值相对于总投资较少
那么交易费可以简化为pi*xi
所以净收益可以简化为(ri-pi)*xi
3.目标是净收益尽量大,总体风险尽量小
那么可以得出目标函数是
收益最大 max∑(ri-pi)*xi
风险最小 min max{qixi}
约束条件是
总投资额为M ∑(1+pi)*xi=M
投资量大于0 xi>=0,i=0,1...n
可以做出三种模型,将多目标规划变成一个目标的线性规划
一.固定风险水平,优化收益
投资中需要设立一个风险界限a,为最大可承受风险。
由于总体风险用投资项目中最大的一个风险来度量
所以每一个风险qi*xi都需要小于等于a

二.固定盈利水平,极小化风险
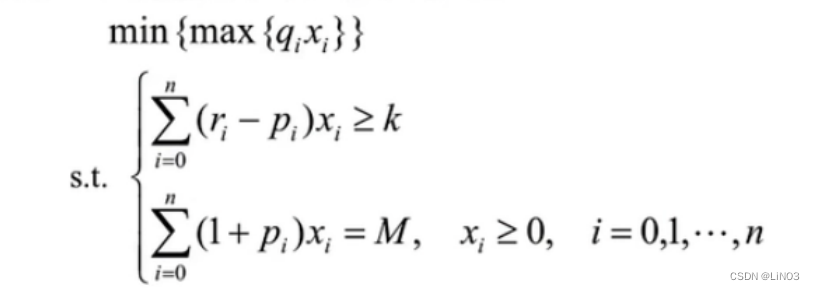
三.设置一个投资偏好系数S
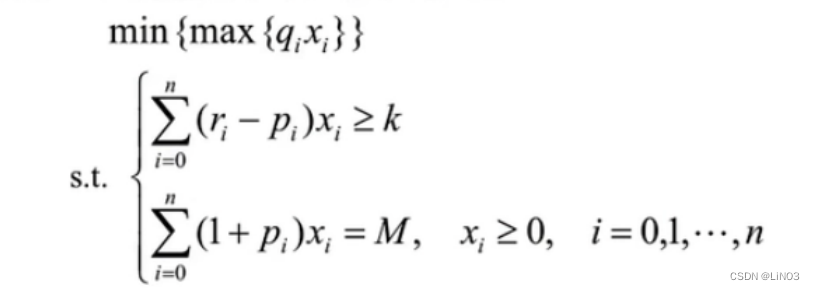
求解:
对模型一进行求解

设风险度a<0.5
从0开始步长为0.001
语法解析
clc 清理命令行
clear 清空工作空间workspace的所有变量
hold on 添加新绘图的时候保留当前绘图
hold off 使当前轴及图像不再具备被刷新的性质,新图出现时,取消原图。即,关闭图形保持功能。
MATLAB中
while循环while 条件表达式 执行语句 endzeros
diag函数生成对角矩阵
diag([主对角元素,,,,])
X = ones返回标量1。
X = ones(n)返回一个n×n的全 1 矩阵。x = ones(a,b)返回一个a*b的矩阵
plot 二维线图
plot(x,y)创建
Y中数据对X中对应值的二维线图。
要绘制由线段连接的一组坐标,请将
X和Y指定为相同长度的向量。要在同一组坐标区上绘制多组坐标,请将
X或Y中的至少一个指定为矩阵。plot(x,y,线型、标记和颜色)创建
Y中数据对X中对应值的二维线图。二维线图 - MATLAB plot - MathWorks 中国
xlabel :为x轴加标签
ylabel:为y轴加标签
A=
A=[zeros(4,1),diag([-0.025,0.015,0.055,0.026])];B=
代码
clc,clear
a=0;hold on
while a<0.05
c=[-0.05,-0.27,-0.19,-0.185,-0.185];
A=[zeros(4,1),diag([0.025,0.015,0.055,0.026])];
b=a*ones(4,1);
Aeq=[1,1.01,1.02,1.045,1.064];
beq=1;
lb=zeros(5,1);
[x,Q]=linprog(c,A,b,Aeq,beq,lb);
Q=-Q;
plot(a,Q,'*k');
a=a+0.001;
end
xlabel('a'),ylabel('Q')
输出结果



结论
计算转折点a=0.006时,x的值
clc,clear
a=0.006
c=[-0.05,-0.27,-0.19,-0.185,-0.185];
A=[zeros(4,1),diag([0.025,0.015,0.055,0.026])];
b=a*ones(4,1);
Aeq=[1,1.01,1.02,1.045,1.064];
beq=1;
lb=zeros(5,1);
[x,Q]=linprog(c,A,b,Aeq,beq,lb);
Q=-Q;
x
0
0.240000000000000
0.400000000000000
0.109090909090909
0.221428571428571
Q
0.201946103896104