代码随想录-刷题第五十二天

news2025/1/18 9:11:22

300. 最长递增子序列

题目链接：300. 最长递增子序列

思路：动态规划五步曲：

dp[i]表示从0到i，以nums[i]结尾的最长递增子序列的长度。
递推公式：if(nums[i]>nums[j]) dp[i] = max(dp[i], dp[j] + 1)

位置i的最长升序子序列等于j从0到i-1各个位置的最长升序子序列 + 1 的最大值。

注意这里不是 dp[i] 与 dp[j] + 1 进行比较，而是要取 dp[j] + 1 的最大值。
初始化：dp[i]都初始化为1

每一个i，对应的dp[i]（即最长递增子序列）起始大小至少都是1。
遍历顺序：从递推公式可以看出需要从前向后遍历。

dp[i] 是有 0 到 i-1 各个位置的最长递增子序列推导而来，那么遍历i一定是从前向后遍历。

j其实就是遍历 0 到 i-1，那么是从前到后，还是从后到前遍历都无所谓，只要把 0 到 i-1 的元素都遍历了就行，所以默认习惯从前向后遍历。
举例推导dp数组

输入：[0,1,0,3,2]，dp数组的变化如下：

如果代码写出来，但一直AC不了，那么就把dp数组打印出来，看看对不对！

class Solution {
    public int lengthOfLIS(int[] nums) {
        // dp[i] 表示以 nums[i] 这个数结尾的最长递增子序列的长度
        int[] dp = new int[nums.length];
        // dp 数组全都初始化为 1
        Arrays.fill(dp, 1);
        int res = 1;

        for (int i = 0; i < nums.length; i++) {
            for (int j = 0; j < i; j++) {
                if (nums[i] > nums[j]) {
                    dp[i] = Math.max(dp[i], dp[j] + 1);
                }
                if (dp[i] > res) res = dp[i]; // 取长的子序列
            }
        }
        
        return res;
    }
}

674. 最长连续递增序列

题目链接：674. 最长连续递增序列

思路：本题相对于上一题来说多了一个连续的条件，动态规划五步曲：

dp[i] 表示从0到i，以nums[i]为结尾的最长连续递增子序列长度。

注意这里的定义，一定是以下标i为结尾，并不是说一定以下标0为起始位置。
递推公式：if(nums[i] > nums[i - 1]) dp[i] = dp[i - 1] + 1

如果 nums[i] > nums[i - 1]，那么以 i 为结尾的连续递增的子序列长度一定等于以i - 1为结尾的连续递增的子序列长度 + 1 。

因为本题要求连续递增子序列，所以就只要比较nums[i]与nums[i - 1]，而不用去比较nums[j]与nums[i] （j是在0到i之间遍历）。

既然不用j了，那么也不用两层for循环，一层for循环就行，比较nums[i] 和 nums[i - 1]。
初始化：dp[i]都初始化为1

以下标i为结尾的连续递增的子序列长度最少也应该是1，即就是nums[i]这一个元素。
遍历顺序：从递推公式可以看出需要从前向后遍历。
举例推导dp数组

以输入nums = [1,3,5,4,7]为例，dp数组状态如下：

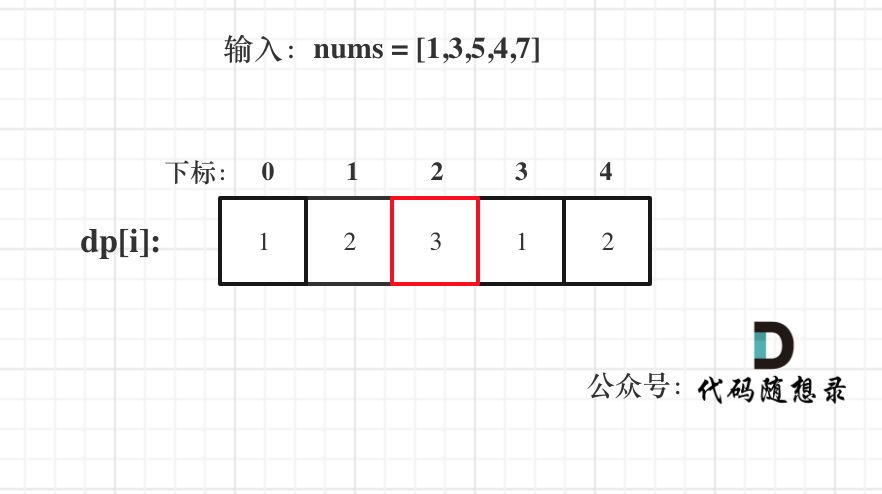
注意这里要取dp[i]里的最大值，所以dp[2]才是结果！

class Solution {
    public int findLengthOfLCIS(int[] nums) {
        // dp[i] 表示以nums[i]为结尾的最长连续递增子序列长度
        int[] dp = new int[nums.length];
        // dp 数组全都初始化为 1
        Arrays.fill(dp, 1);
        int res = 1;
        
        for (int i = 1; i < nums.length; i++) {
            if (nums[i] > nums[i - 1]) {
                dp[i] = dp[i - 1] + 1;
            }
            if (dp[i] > res) res = dp[i]; // 取长的连续递增子序列
        }
        return res;
    }
}

这道题目也可以用贪心来解决

class Solution {
    public static int findLengthOfLCIS(int[] nums) {
        int res = 1; // 连续子序列最少也是1
        int count = 1;
        for (int i = 1; i < nums.length; i++) {
            if (nums[i] > nums[i - 1]) { // 连续记录
                count++;
            } else { // 不连续，count从头开始
                count = 1;
            }
            if (count > res) res = count;
        }
        return res;
    }
}

718. 最长重复子数组

题目链接：718. 最长重复子数组

思路：注意题目中说的子数组，其实就是连续子序列。动态规划五步曲：

dp[i][j] ：以下标i - 1为结尾的A和以下标j - 1为结尾的B，最长重复子数组的长度为dp[i][j]。

特别注意：“以下标i - 1为结尾的A” 表明一定是以A[i - 1]为结尾的子数组。

dp[0][0]是什么含义呢？总不能是以下标-1为结尾的A数组吧。

其实dp[i][j]的定义也就决定着，在遍历dp[i][j]的时候i 和 j都要从1开始。
递推公式：if(nums1[i - 1] == nums2[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1

根据dp[i][j]的定义，dp[i][j]的状态只能由dp[i - 1][j - 1]推导出来

即当A[i - 1]和B[j - 1]相等的时候，dp[i][j] = dp[i - 1][j - 1] + 1
初始化：dp[i][0]和dp[0][j]初始化为0。

根据dp[i][j]的定义，dp[i][0] 和dp[0][j]其实都是没有意义的！

但dp[i][0] 和dp[0][j]要初始值，为了方便递归公式dp[i][j] = dp[i - 1][j - 1] + 1，所以dp[i][0]和dp[0][j]初始化为0。
遍历顺序：需要从前向后遍历，先遍历i或者j都可以。
举例推导dp数组

以A: [1,2,3,2,1]，B: [3,2,1,4,7]为例，画一个dp数组的状态变化，如下：

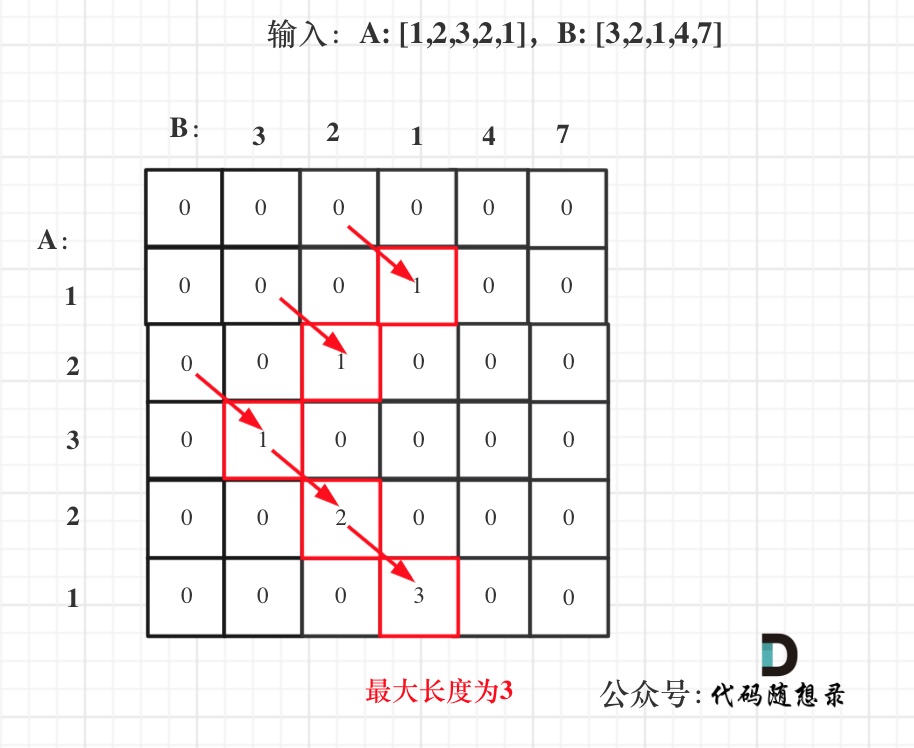
class Solution {
    public int findLength(int[] nums1, int[] nums2) {
        int m = nums1.length, n = nums2.length;
        int res = 0;
        int[][] dp = new int[m + 1][n + 1];
        
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                if (nums1[i - 1] == nums2[j - 1]) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                }
                if (dp[i][j] > res) res = dp[i][j];
            }
        }
        
        return res;
    }
}