原理

无失真编码中的算术编码是一种用于将输入数据进行高效压缩的方法，同时保留了原始数据的完整性。
算术编码的实现过程如下：

1. 数据分段：首先，将要进行编码的数据划分为一个个符号或字符。每个符号可以是文本中的一个字母、一幅图像中的一个像素或其他数据单元，具体取决于应用场景。

2. 计算符号概率：对于每个符号，需要计算其在数据中出现的概率。通常，这些概率是基于统计数据中每个符号的出现频率来估计的。

3. 构建累积概率表：根据符号的概率，构建一个累积概率表。这个表将每个符号映射到一个累积概率区间，其长度与符号的概率相关。通常，累积概率表是一个包含0到1之间所有可能区间的表格。

4. 编码过程：算术编码的编码过程从0到1的一个初始区间开始。然后，根据输入数据中的每个符号，不断地缩小当前区间，使其逐渐趋近于一个特定的数值。编码的方式是根据当前符号的累积概率区间来调整当前区间的大小。具体步骤如下：

5. 对于每个输入符号，找到其在累积概率表中对应的区间。

6. 将当前区间按照符号的概率进行分割，使得当前区间缩小到符号对应的区间范围内。

7. 重复以上两步，直到处理完所有输入符号。

8. 编码结果：最终，算术编码会产生一个介于0和1之间的小数，这个小数可以用二进制或其他形式的编码表示。通常，这个编码是一个无限小数，但实际上会截断为有限长度，以方便存储或传输。编码后的数据可以通过解码过程来还原成原始数据。

python实现下图结果

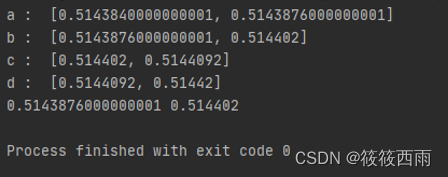
提示

所示结果图中有两部分内容，一是对消息序列中最后一个符号编码后得到的各符号子区间，二是对消息序列编码完成后得到的子区间的上下边界。信源符号及概率分布可由一个字典表示，待编码消息序列为”cadacdb”，如

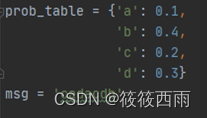
python代码

import numpy as np

prob_table = {'a': 0.1,
              'b': 0.4,
              'c': 0.2,
              'd': 0.3}
msg = 'cadacdb'

def process_stage(low, high):
    stage_len = high - low
    stage_prob = {}
    for key in prob_table:
        cum_prob = low + stage_len * prob_table[key]
        stage_prob[key] = [low, cum_prob]
        low = cum_prob

    return stage_prob

low = 0.0
high = 1.0

encoder = []

for ch in msg:
    stage_prob = process_stage(low, high)
    low = stage_prob[ch][0]
    high = stage_prob[ch][1]

    encoder.append(stage_prob)

for key, value in encoder[-1].items():
    print(key, ': ', value)
print(low, high)

结果展示

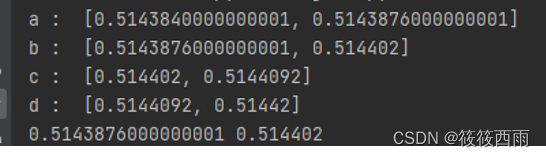
总结

算术编码的本质是为整个输入序列分配一个码字，而不是给每个字符分别指定码字，因此平均意义上可以为单个字符分配码长小于1的码字。
算术编码用到两个基本的参数：符号的概率和它的编码间隔。信源符号的概率决定压缩编码的效率，也决定编码过程中信源符号的间隔，而这些间隔包含在L到H之间。编码过程中的间隔决定了符号压缩后的输出。
给定事件序列的算术编码步骤如下：
1.编码器在开始时将“当前间隔”设置为[ L， H)；
2.对每一事件，编码器按步骤a）和b）进行处理：
a) 编码器将“当前间隔”分为子间隔，每一个事件一个；
b) 一个子间隔的大小与下一个将出现的事件的概率成比例，编码器选择子间隔对应于下一个确切发生的事件相对应，并使它成为新的“当前间隔”；
3.最后输出的“当前间隔”的下边界和上边界之间的一个合适的值就是该给定事件序列的算术编码。